6.5. Confidence intervals for the mean of a normal distribution:

population variance unknown: small sample size

In previous topics we discussed inferences about a population mean when a large sample is available. Those methods are deeply rooted in the central limit theorem, which guarantees that the distribution of is approximately normal.

Many investigations require statistical inferences to be drawn from small samples (n <30). Since the sample mean will still be used for inferences about , we must address the question, “what is the sampling distribution of when n is not large?”. Unlike the large sample situations, here we do not have an unqualified answer, and central limit theorem is no longer applicable.

6.5.1. Student’s t distribution

Consider a sampling situation where the population has a normal distribution with unknown . Because is unknown, an intuitive approach is to estimate by the sample standard . Just as we did in the large sample situation, we consider the ratio

This random variable does not follow a standard normal distribution. Its distribution is known as Student’s t distribution.

The graph of the t-distribution resembles the graph of the standard normal distribution: they both are symmetric, bell shaped curves with mean equal to zero. The graph of the Student’s t distribution is lower at the center and higher at the extremities than the standard normal curve. (Fig. 6.4).

The new notation t is required in order to distinguish it from the standard normal variable Z. As the number of degrees of freedom increases, the difference between t distribution and the standard normal distribution becomes smaller and smaller.

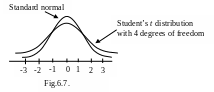
The qualification “with (n -1) degrees of freedom” is necessary, because with each different sample size or value of ( n -1), there is a different t distribution.

Definition:

The number of degrees of freedom is defined as the number of observations that can be chosen freely.

Example:

Suppose we know that the mean number of 5 values is 25. Consequently, the sum of these 5 values is 125 . Now how many values out of 5 can be chosen freely so that the sum of these 5 values is 125? The answer is that we can freely choose 5-1=4 values. Suppose we choose 15, 35, 45, and 10 as the 4 values. Given these 4 values and the information that the mean of the 5 values is 25, the value is

Thus, once we have chosen 4 values, the fifth value is automatically determined. Consequently, the number of degrees of freedom for this example is

We subtract 1 from n because we lose one degree of freedom to calculate the mean.

The t- table in the Appendix (see table 4) is arranged to give the value t for several frequently used values of and for a number of values ( n -1).

Definition:

A random variable having the standard distribution with ( Greek letter nu)

Degrees of freedom will be denoted by (Fig. 6.8). Then is defined as the number for which

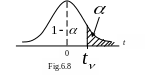
Example: Find

Solution:

In words it means we need to find a number that is exceeded with the probability 0.10 by a Student’s t random variable with 5 degrees of freedom.

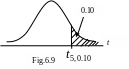
From table 4 of the Appendix we read that . (Fig. 6.9).

Similarly, to for Student’s t distribution the value is defined as

.