- •Тульский государственный университет
- •Методические указания
- •1. Введение.
- •2. Цели и задачи.
- •3. Задание на курсовую работу.
- •4. Объем и содержание курсовой работы.
- •5. Выполнение курсовой работы.
- •6. Защита курсовой работы.
- •7. Методические указания к выполнению
- •8. Оформление пояснительной записки.
- •9. Оформление графической части
- •10. Метод верхней оценки усилий
- •11. Варианты Заданий на курсовую работу (часть 1)
- •12. Метод осредненных напряжений
- •13. Варианты Заданий на курсовую работу
- •13. Исходные данные
- •Основной
- •Дополнительный
- •«Теория обработки металлов давлением»
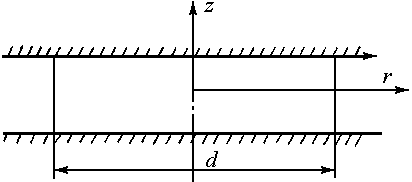
- •Прессование полосы в гладкой конической матрице
13. Варианты Заданий на курсовую работу
Задача 2.1. Определить удельное
усилие осадки призматической заготовки
шириной
,
высотой
и длиной
![]()
![]() (рис. 2.1). На границе контакта справедлив
закон прадтлева трения
(рис. 2.1). На границе контакта справедлив
закон прадтлева трения
![]()
Рис. 2.1
|
Решение. Предполагаем, что
касательное напряжение
|
Принимая деформированное состояние плоским, условие текучести запишем в следующем виде:
![]() .
.
При этих предположениях из системы дифференциальных уравнений равновесия
![]()
остается лишь одно первое, второе
уравнение тождественно удовлетворяется.
Проинтегрируем первое уравнение по
от
![]() до
до
![]() :
:
![]() .
.
Тогда получим
![]()
![]() .
.
Используя условие текучести, находим
![]() (2.1)
(2.1)
Подставляя в уравнение (2.1) граничные
условия для касательных напряжений,
т.е.![]() ,
получаем
,
получаем
![]() .
(2.2)
.
(2.2)
Интегрирование выражения (2.2) приводит к виду
![]() .
.
Из условия, что при
![]()
![]() ,
а
,
а
![]() ,
определяют постоянную интегрирования:
,
определяют постоянную интегрирования:
![]() ;
;
![]() (2.3)
(2.3)
Полное усилие осадки найдем интегрированием (2.3) от 0 до /2:
![]()
Удельное усилие осадки определим по уравнению
![]()
Задача 2.2. Определить удельное
усилие осадки призматической заготовки
(рис.2.1), если на границе контакта
справедлив закон линейного изменения
касательного напряжения
![]() .
.
Решение. Используя уравнение равновесия (2.1), полученное при решении предыдущей задачи, и подставляя в него выражение для , получаем
![]() (2.4)
(2.4)
Интегрируя уравнение (2.4), приходим к соотношению
![]() .
.
Из условия, что при , , находим постоянную интегрирования:
![]() ;
;
![]()
Удельное усилие осадки определим следующим образом:
![]()
Задача 2.3. Определить удельное
усилие осадки цилиндрической заготовки
диаметром
![]() и высотой
(рис.2.2, а), если на границе контакта
справедлив закон прандтлева трения
и высотой
(рис.2.2, а), если на границе контакта
справедлив закон прандтлева трения
![]() .
.
Решение. Предполагаем, что при
изменении от
![]() до
касательное напряжение изменяется от
до
до
касательное напряжение изменяется от
до
![]() на контактных поверхностях, и допускаем,
что напряжение
на контактных поверхностях, и допускаем,
что напряжение
![]() и
и
![]() не зависит от
.
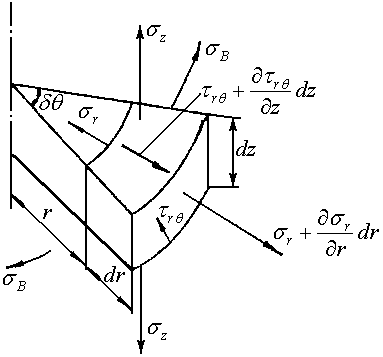
В этом случае уравнение равновесия
элементарного сектора (рис.2.2, б) можно
записать в виде
не зависит от
.
В этом случае уравнение равновесия
элементарного сектора (рис.2.2, б) можно
записать в виде
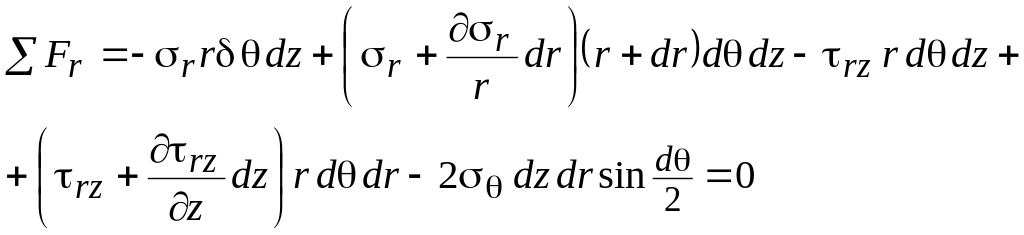
или
![]()
Так как в задаче реализуется осесимметричное напряженное состояние, то предполагаем, что имеет место условие полной пластичности, т.е.
![]() .
(2.5)
.
(2.5)
С учетом условия (2.5) уравнение равновесия перепишется в виде
![]() .
(2.6)
.
(2.6)
Проинтегрируем уравнение (2.6) от до :
![]() ,
,
и получим
![]() (2.7)
(2.7)
Подставляя в уравнение (2.7) граничные условия для трения, перепишем это уравнение в виде
![]() .
.
а)
б) Рис. 2.2
|
В случае осесимметричного напряженного состояния в предположении полной пластичности условие текучести имеет вид:
Учитывая (2.8), уравнение (2.7) записываем так:
Интегрирование выражения (2.9) позволяет получить закон изменения нормальных напряжений на границе контакта:
Из условия, что при
Деформирующую силу определим из следующего выражения: |
![]()
Удельное усилие процесса
![]() .
.
Задача 2.4. Определить удельное усилие осадки цилиндрической заготовки (рис.2.2), если на поверхности контакта справедлив следующий закон изменения касательных напряжений:
![]() .
.
Решение. Проводя аналогичные преобразования, как и в предыдущей задаче, уравнение равновесия для данного случая можно записать в виде
![]() .
.
Интегрируя это выражение, получаем
![]() .
.
Постоянную интегрирования определим
из условия, что при
![]()
Тогда
![]()
![]() .
.
Полное усилие процесса определим следующим образом:
![]() .
.
Удельное усилие процесса
![]()
Задача 2.5. Определить удельное
усилие открытой прошивки плоским
пуансоном диаметром
,
цилиндрической заготовки диаметром
![]() (рис. 2.3). Предполагаем, что на поверхности
контакта пуансона и заготовки справедлив
закон Прадтлева трения
(рис. 2.3). Предполагаем, что на поверхности
контакта пуансона и заготовки справедлив
закон Прадтлева трения
![]() .
.
Решение. Допускаем, что часть деформируемой заготовки, непосредственно находящейся под воздействием пуансона, подвергается осаживанию, которому препятствует кольцевая часть, окружающая металл.
Тогда, используя уравнение равновесия для случая свободной осадки цилиндрических заготовок и закон трения на контактной поверхности, получаем следующее дифференциальное уравнение:
Интегрируя его, определяем
Постоянная интегрирования находится из условия, что на границе цилиндрической и кольцевой частей радиальные напряжения равны между собой. Из условия текучести следует
|
Рис. 2.3 |
При
![]() ,
,
где
![]() - сопротивление (сжимающее напряжение),
вызываемое кольцевой частью.
- сопротивление (сжимающее напряжение),
вызываемое кольцевой частью.
Тогда
![]()
Окончательно нормальное напряжение определим следующим образом:
![]()
Деформирующая сила
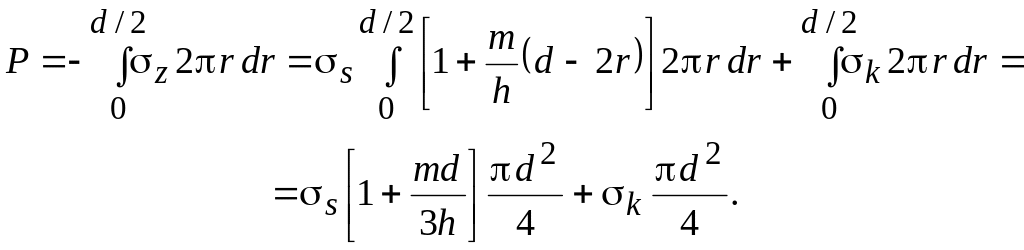
Удельное усилие
![]() .
.
Для определения напряжения
![]() предположим, что кольцевая часть
заготовки не испытывает осевой деформации,
т.е.
предположим, что кольцевая часть
заготовки не испытывает осевой деформации,
т.е.
![]() .
В этом случае уравнение равновесия
запишется в виде
.
В этом случае уравнение равновесия
запишется в виде
![]() (2.10)
(2.10)
а условие текучести
![]() (2.11)
(2.11)
Решая совместно уравнения (2.10) и (2.11),
определяем постоянную интегрирования
из условия, что при
![]() .
Найдем
.
Найдем
![]() .
.
Величину
определим, полагая
![]() и
и
![]() :
:
![]()
Окончательно удельное усилие открытой прошивки
![]()
Рис. 2.4
|
Задача 2.6. Определить усилие закрытой прошивки плоским пуансоном (рис. 2.4). На границе контакта материала заготовки и инструмента справедлив закон прадтлева трения. Решение. Предполагаем, что при движении пуансона происходит осаживания металла, находящегося под непосредственным воздействием пуансона, в результате чего металл затекает в кольцевую полость между стенками матрицы и пуансона. Решая задачу аналогично предыдущей, получаем выражение для удельного усилия процесса: |
![]()
где
![]() - напряжение, возникающее на границе
кольцевой и цилиндрической частей и
препятствующее осаживанию последней.
- напряжение, возникающее на границе
кольцевой и цилиндрической частей и
препятствующее осаживанию последней.
Условие текучести для кольцевой части может быть записано следующим образом:
![]()
где
![]() и
и
![]() -
напряжения, действующие в кольцевой
полости.
-
напряжения, действующие в кольцевой
полости.
Условно допускаем равномерное
распределение этих напряжений в области
![]() Тогда напряжение
определит сопротивление, которое
необходимо преодолеть для продвижения
металла в кольцевой части полости.
Тогда напряжение
определит сопротивление, которое
необходимо преодолеть для продвижения
металла в кольцевой части полости.
Выделив в кольцевой части бесконечно малый элемент и приняв условие постоянство силы трения
![]()
получим уравнение равновесия бесконечно малого элемента:
![]()
или
![]() (2.12)
(2.12)
Проинтегрировав уравнение (2.12), получим
![]()
Из условия, что на свободной поверхности
металла
![]() ,
найдем произвольную постоянную:
,
найдем произвольную постоянную:
![]()
![]() (2.13)
(2.13)
Сопротивление кольцевой части заготовки
определим из выражения (2.13), полагая
![]() .
.
Тогда из условия текучести имеем:
![]()
Окончательное удельное усилие закрытой прошивки будет
![]()
Задача 2.7. Определить удельное
усилие волочения полосы через клиновую
матрицу с малым углом раствора
![]() при условии трения кулона на контактной
поверхности (коэффициент трения
мал).
при условии трения кулона на контактной
поверхности (коэффициент трения
мал).
Решение. Составим приближенное уравнение равновесия элемента деформируемого тела, выделенного двумя плоскими сечениями и шириной, равной 1 (рис. 2.5):
![]()
или
![]()
Учитывая, что
![]()
находим
![]() .
(2.14)
.
(2.14)
Если угол матрицы и коэффициент трения малы, то можно приближенно считать, что
Тогда условие пластичности для плоского деформированного состояния можно записать так:
|
Рис. 2.5
|
Исключив
![]() из соотношения (2.14) с помощью условий
(2.15) и разделив переменные, найдем
из соотношения (2.14) с помощью условий
(2.15) и разделив переменные, найдем
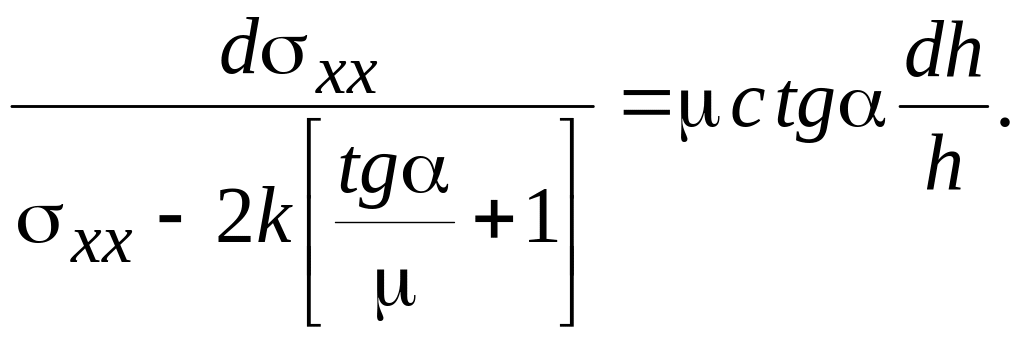 (2.16)
(2.16)
После интегрирования уравнения (2.16) с последующим его потенцированием получим
![]() (2.17)
(2.17)
Константу интегрирования определим из
граничных условий при
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() .
(2.18)
.
(2.18)
Умножим уравнение (2.18) на величину
![]() ,
вычтем его из соотношений (2.17) и получим
,
вычтем его из соотношений (2.17) и получим
 .
(2.19)
.
(2.19)
Удельное усилие волочения определим с
помощью выражения (1.31) после подстановки
в него
![]() :
:
 (2.20)
(2.20)
Рис. 2.6 |
Отметим, что если волочение полосы
осуществляется в матрице без трения,
т.е.
Оно по величине равно идеальной работе пластической деформации изменения размеров полосы.
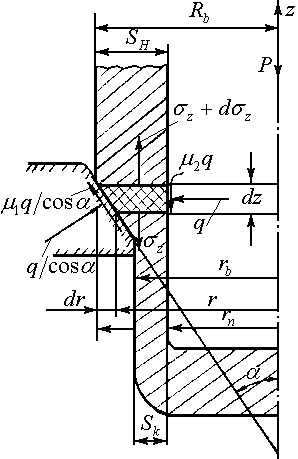
Задача 2.8. Определить удельное
усилие процесса вытяжки с утонением
стенки цилиндрического стакана через
коническую матрицу с углом
(рис. 2.6. В результате деформации
начальная толщина стенки стакана
|
Решение. Предполагаем, что
горизонтальные составляющие радиальных
сжимающих напряжений
![]() от реактивных сил на контактных
поверхностях матрицы и пуансона
принимаются одинаковыми по величине.
от реактивных сил на контактных
поверхностях матрицы и пуансона
принимаются одинаковыми по величине.
Тогда уравнение равновесия элементарного кольцевого участка, расположенного в очаге деформации, запишется в виде
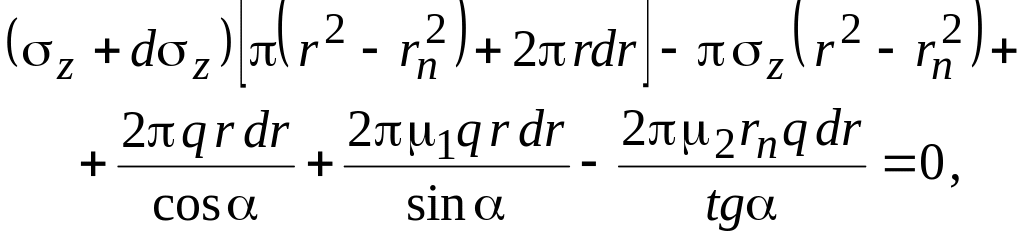
где
![]() и
и
![]() - коэффициенты трения на внешней и
внутренней поверхностях полуфабриката.
- коэффициенты трения на внешней и
внутренней поверхностях полуфабриката.
Проведя преобразования, получим
![]() (2.21)
(2.21)
Без большой погрешности можно произвести следующую замену:
![]()
![]()
Введя обозначение
![]() (2.22)
(2.22)
преобразуем уравнение (2.22) к виду
![]() (2.23)
(2.23)
Считая угол матрицы малым, а коэффициент трения умеренным, можно приближенно принять
![]()
![]()
Тогда из условия текучести получим
![]() (2.24)
(2.24)
Подставив выражение (2.24) в равенство (2.23), найдем
![]() . (2.25)
. (2.25)
Проинтегрируем уравнение (2.25) при
условии, что на верхней границе очага
деформации
![]() .
В этом случае
.
В этом случае


Тогда рабочее напряжение определим по формуле