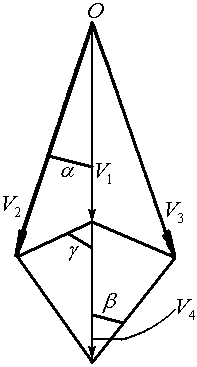- •Тульский государственный университет
- •Методические указания
- •1. Введение.
- •2. Цели и задачи.
- •3. Задание на курсовую работу.
- •4. Объем и содержание курсовой работы.
- •5. Выполнение курсовой работы.
- •6. Защита курсовой работы.
- •7. Методические указания к выполнению
- •8. Оформление пояснительной записки.
- •9. Оформление графической части
- •10. Метод верхней оценки усилий
- •11. Варианты Заданий на курсовую работу (часть 1)
- •12. Метод осредненных напряжений
- •13. Варианты Заданий на курсовую работу
- •13. Исходные данные
- •Основной
- •Дополнительный
- •«Теория обработки металлов давлением»
- •Прессование полосы в гладкой конической матрице
11. Варианты Заданий на курсовую работу (часть 1)
Задача
1.1. Найти
усилие осадки пластически однородной
полосы между двумя жесткими плитами,
сближающимися со скоростями
![]() .
Известны
размеры полосы
.
Известны
размеры полосы
![]() и
и
![]() ,
а также предел текучести материала
полосы при сдвиге к.
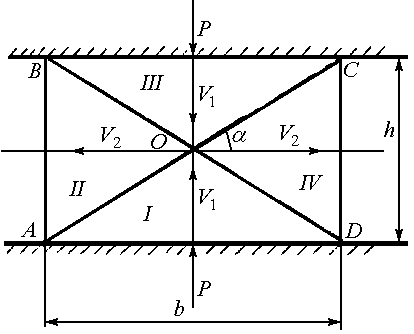
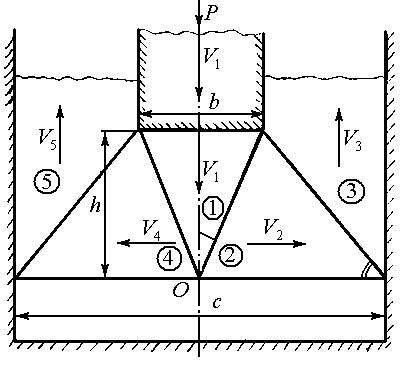
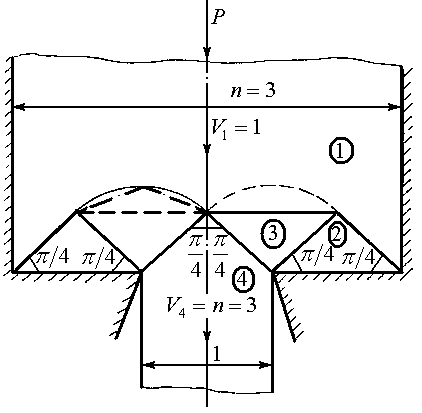
Схема процесса осадки пластически
однородной полосы и кинематически
допустимое поле скоростей показаны на
рис. 1.1а.
,
а также предел текучести материала
полосы при сдвиге к.
Схема процесса осадки пластически
однородной полосы и кинематически
допустимое поле скоростей показаны на
рис. 1.1а.
а |
б |
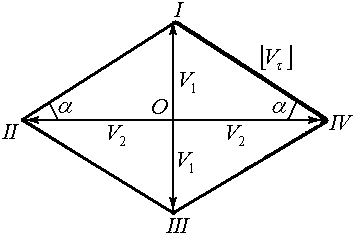
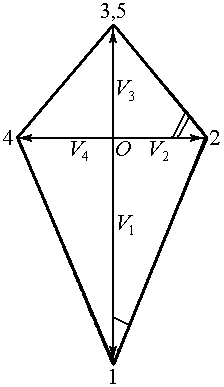
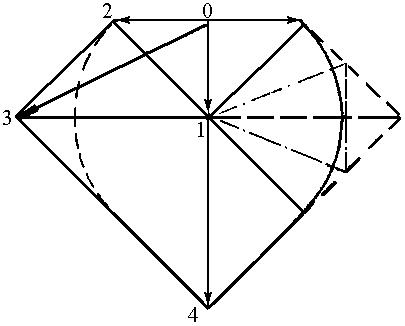
Рис. 1.1 Схема операции осадки (а) и годограф скоростей (б) |
|
Решение.
Предполагаем, что длина
![]() полосы значительно больше ширины
и толщины
,
т.е.
полосы значительно больше ширины
и толщины
,
т.е.
![]() ,
так что деформацию можно считать плоской.
В поперечном сечении линии ОА, ОВ, ОС,
ОD являются линиями разрыва скоростей
(следами плоскостей разрыва,
перпендикулярными плоскости чертежа).
,
так что деформацию можно считать плоской.
В поперечном сечении линии ОА, ОВ, ОС,
ОD являются линиями разрыва скоростей
(следами плоскостей разрыва,
перпендикулярными плоскости чертежа).
В силу условия несжимаемости на этих линиях непрерывны нормальные составляющие скоростей, а разрывы касательных составляющих, как это следует из годографа скоростей (рис. 1.1б), определяется следующим образом:
![]() .
.
Длина любой линии разрыва
![]() .
.
Определим суммарную мощность разрыва
![]() .
(1.9)
.
(1.9)
Мощность внешних сил
![]() ,
,
где
![]() и
и
![]() - усилие и удельное усилие осадки полосы.
- усилие и удельное усилие осадки полосы.
По теореме о верхних оценках
![]() .
.
Отсюда находим
![]() ,
,
т.е.
верхняя оценка
![]() удельного усилия осадки составляет
удельного усилия осадки составляет
![]() .
(1.10)
.
(1.10)
Верхние оценки усилия и мощности осадки.
![]() .
(1.11)
.
(1.11)
Задача
1.2. Найти
усилие вдавливания жесткого плоского
штампа в пластическое полупространство.
Деформацию считать плоской. Предел
текучести материала при сдвиге равен
![]() .
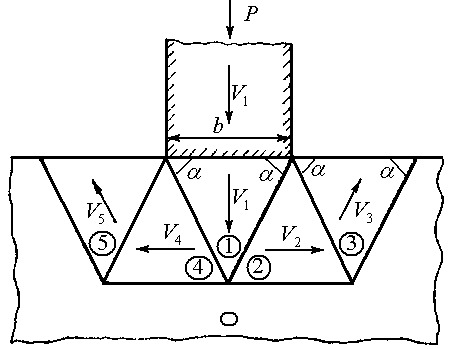
Схема процесса выдавливания и кинематически
допустимое поле скоростей показаны на
рис. 1.2а.
.
Схема процесса выдавливания и кинематически
допустимое поле скоростей показаны на
рис. 1.2а.
Решение.
Поле скоростей
характеризуется единственным параметром
– углом
![]() ,
подлежащим определению из условия
минимума мощности деформации.
,
подлежащим определению из условия
минимума мощности деформации.
а |
б |
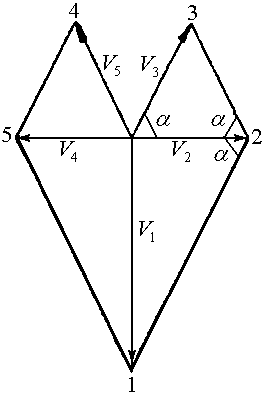
Рис. 1.2 Схема операции (а) и годограф скоростей (б) |
|
Из годографа скоростей (рис. 1.2б) следует
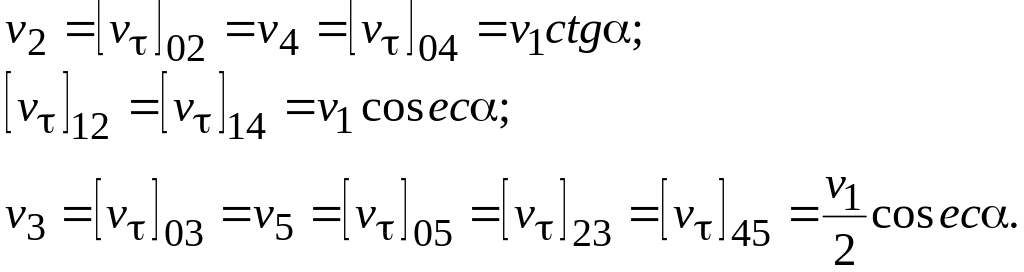 .
.
Определяем длины линий разрыва:
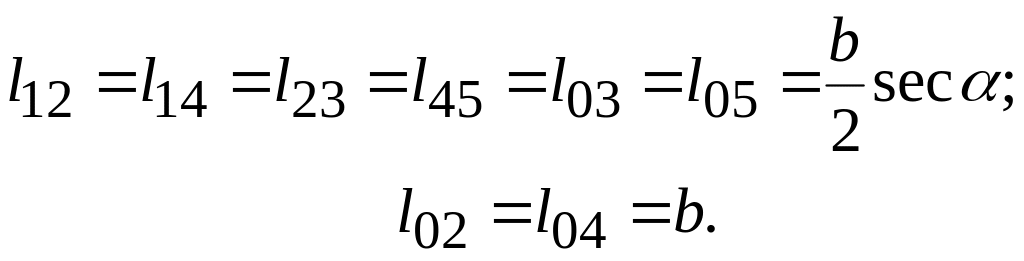
![]() .
.
Находим мощность разрыва
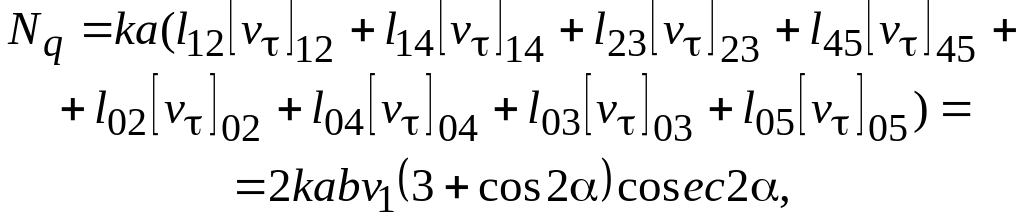
где - размер штампа в направлении, перпендикулярном к плоскости рисунка.
Мощность внешних сил
![]() .
.
По теореме о внешних оценках получаем
![]() .
.
Угол , при котором имеет минимум, найдем из уравнения
![]() ,
,
получающего после преобразований вид
![]() .
.
Отсюда следует
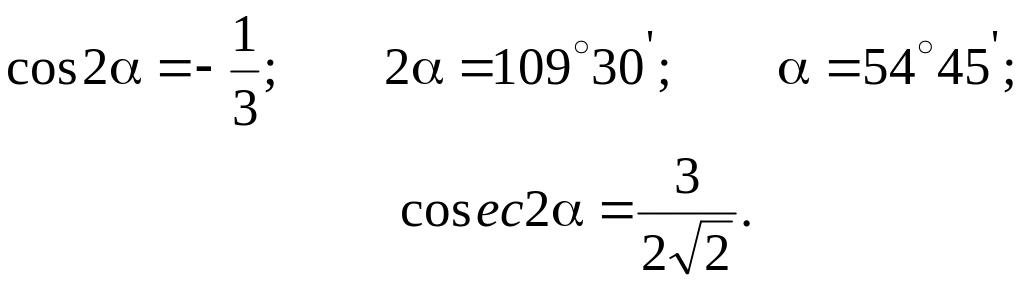 .
.
Легко проверить, что при найденном значении
![]() ,
,
что соответствует минимуму .
Верхняя оценка удельного усилия при этом будет
![]() ,
(1.12)
,
(1.12)
Верхние оценки усилия и мощности вдавливания штампа в пластическое полупространство находятся по формулам:
.
Задача
1.3. Найти
усилие закрытой прошивки полосы
пуансоном, перемещающимся относительно
контейнера со скоростью
![]() .
Предел текучести материала полосы при
сдвиге равен
.
Геометрические размеры инструмента
известны. Трением пренебречь. Схема
процесса закрытой прошивки полосы
показана на рис. 1.3а.
.
Предел текучести материала полосы при
сдвиге равен
.
Геометрические размеры инструмента
известны. Трением пренебречь. Схема
процесса закрытой прошивки полосы
показана на рис. 1.3а.
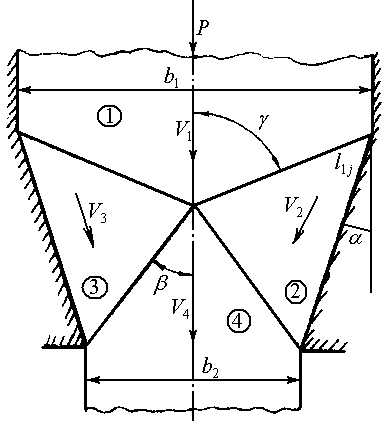
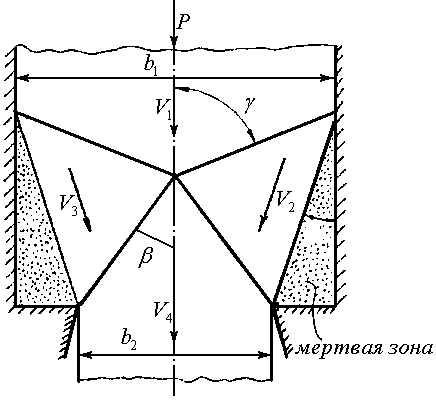
Решение. Кинематически допустимое поле скоростей в этом случае зависит от параметра (рис.1.3а), физический смысл которого состоит в том, что определяет глубину проникновения пластической деформации.
Из годографа скоростей (рис. 1.3б) следует:
![]()
Определяем длины линий разрыва:
![]()
Находим мощность разрыва:
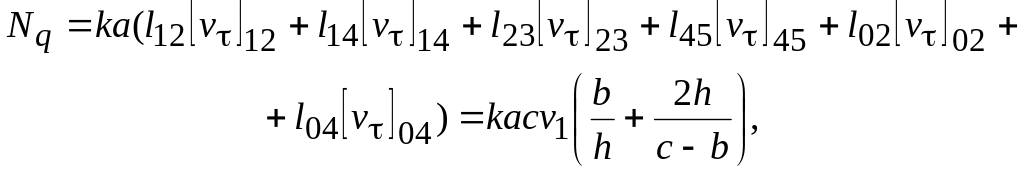
где - размер в направлении, перпендикулярном к плоскости рисунка.
а |
б |
Рис. 1.3 Схема операции прошивки (а) и годограф скоростей (б) |
|
Мощность внешних сил
.
По теореме о верхних оценках получаем
![]() .
.
Наилучшая (т.е. наименьшая) верхняя оценка соответствует значению параметра , определяемого из уравнения
![]() .
.
Отсюда находим
![]() .
.
Подставляя это значение в формулу для , окончательно получаем
![]() .
(1.13)
.
(1.13)
Верхние оценки усилия и мощности находятся по формулам:
.
Задача 1.4 . Найти усилие выдавливания полосы через гладкую клиновую матрицу. Геометрические параметры инструмента заданы. Предел текучести выдавливаемого материала при сдвиге равен .
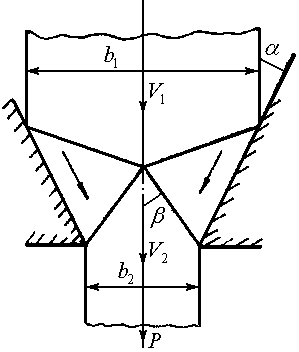
Решение.
Рассмотрим
схему процесса выдавливания полосы
через гладкую клиновую матрицу и
кинематически допустимое поле скоростей
(рис. 1.4а), которому соответствует годограф
скоростей, изображенный на рис. 1.4б. Поле
скоростей зависит от одного параметра,
в качестве которого примем угол
![]() .
Угол
.
Угол
![]() введён для большей наглядности.
введён для большей наглядности.
а |
б |
Рис. 1.4 Схема операции выдавливания (а) и годограф скоростей (б) |
|
Из условия несжимаемости (равенства расходов)
![]()
находим скорость на выходе
![]() ,
,
где
![]() - степень редукции,
- степень редукции,
![]() .
.
Применяя к треугольникам на годографе скоростей теорему синусов, получаем
![]()
![]()
![]()
Определяем длины линий разрыва
![]()
Находим мощность разрыва
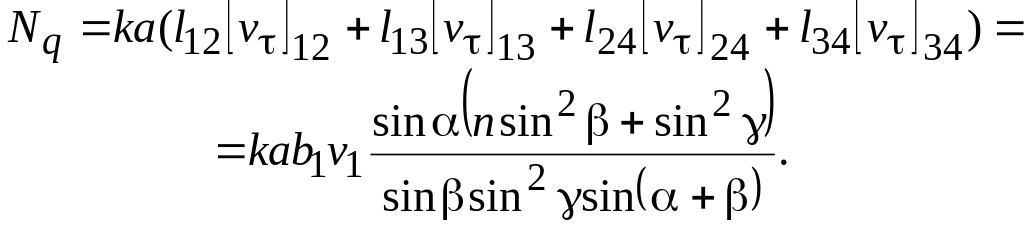
Из геометрических соображений имеем
![]() .
.
Обозначим
![]() .
.
Тогда
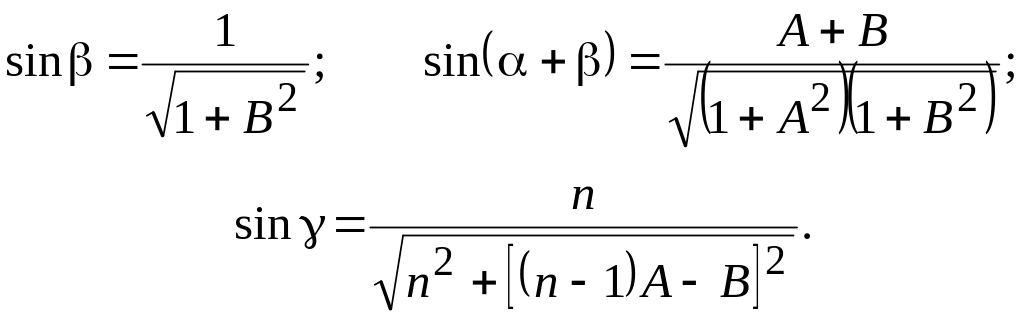
С учетом введенных обозначений выражение мощности разрыва примет вид
![]() .
.
Мощность внешних сил
![]() .
.
По теореме о верхних оценках
![]() .
.
Минимум имеет место при условии
![]() ,
,
так
как параметры
и
![]() взаимно связаны.
взаимно связаны.
Из этого условия получаем
![]()
или
![]() (1.14)
(1.14)
Вводя значение , обеспечивающее минимум , в выражение для находим наилучшую верхнюю оценку удельного усилия выдавливания:
![]() (1.15)
(1.15)
Верхние оценки усилия и мощности находятся по формулам:
.
Задача 1.5. Найти усилие выдавливания полосы через предельно шероховатую клиновую матрицу. Геометрические размеры инструмента и полосы известны. Предел текучести материала и полосы при сдвиге равен .
Решение. Отличие рассматриваемой задачи от предыдущей заключается в том, что теперь необходимо учесть мощность сил трения на границе материала с инструментом в пределах наклоненных участков матрицы.
Длина наклонного участка (см. рис. 1.4) составляет
![]() .
.
Так как матрица предельно шероховата, то удельная сила трения равна , и мощность сил трения будет
![]()
По теореме о верхних оценках получаем
![]() .
.
Отсюда
для верхней оценки удельного усилия
,
используя выражения
![]() и
и
![]() из решения задачи 1.4, находим
из решения задачи 1.4, находим
![]() .
.
Для дальнейшего анализа удобно представить в виде
![]() ,
,
где
![]() .
.
Условие
минимума
по
заключается в равенстве нулю первой
производной
![]() .
Отсюда
.
Отсюда
![]() .
.
После преобразований получаем
![]() .
(1.16)
.
(1.16)
Вводя значение , определенное по формуле (1.16), в выражение для , окончательно находим
![]() .
(1.17)
.
(1.17)
Верхние оценки усилия и мощности находятся по формулам:
.
Задача 1.6. Найти усилие выдавливания полосы через гладкую плоскую матрицу со степенью редукции, равной . Предел текучести материала полосы при сдвиге равен .
Решение.
Рассмотрим схему процесса выдавливания
полосы через гладкую плоскую матрицу
при
![]() (рис. 1.6а). Слева от оси симметрии изображено
поле линий скольжения, справа -
кинематически допустимое поле скоростей,
полученное из поля линий скольжения
заменой дуги окружности отрезка прямой.
(рис. 1.6а). Слева от оси симметрии изображено
поле линий скольжения, справа -
кинематически допустимое поле скоростей,
полученное из поля линий скольжения
заменой дуги окружности отрезка прямой.
а |
б |
Рис. 1.6 Схема операции выдавливания (а) и годограф скоростей (б) |
|
Из годографа скоростей (рис. 1.6б) определяем разрывы скоростей:
![]() .
.
Находим длины линий разрыва:
![]()
Определяем мощность разрыва:
![]()
![]()
Мощность внешних сил
![]()
По теореме о верхних оценках
![]() .
(1.18)
.
(1.18)
Для повышения точности расчетов дугу окружности можно заменить двумя хордами (штрихпунктирные линии), тремя и т.д. Однако объем вычислений при этом увеличивается.
Верхние оценки усилия и мощности находятся по формулам:
.
Задача 1.7. Найти усилие выдавливания полосы через предельно шероховатую плоскую матрицу. Известны геометрические размеры и предел текучести при сдвиге материала полосы .
Рис. 1.7 |
Решение. Рассмотрим схему процесса выдавливания полосы через предварительно шероховатую плоскую матрицу (рис. 1.7). В кинематически допустимом поле скоростей предусмотрена возможность образования мертвых зон, ограниченных прямыми с углами наклона к вертикали. Однако в данном случае угол неизвестен, так как неизвестны заранее размеры мертвых зон.
Поэтому
в этой задаче подлежат определению
из условия минимума
|
Используем выражение для , полученное при решении задачи 1.5:
![]() .
.
Сформулируем условия минимума по и :
![]() .
.
Второму условию удовлетворяет формула (1.16).
Рассмотрим первое условие:
![]() .
.
Имеем
![]()
![]() .
.
После преобразований получаем
![]() ,
(1.19)
,
(1.19)
где
![]() .
.
Приравнивая аргумент арккотангенсов в правых частях формул (1.16) и (1.19), после преобразований находим
![]() .
(1.20)
.
(1.20)
Выражение для имеет смысл, если
![]()
Вычисляем
по формуле (1.20) угол
,
далее по формуле (1.16) находим угол
,
затем определяем величины
,
![]() и
и
![]() :
:
; .
Задача 1.8. Найти силовые параметры процесса волочения полосы, если известны геометрические параметры и предел текучести материала полосы при сдвиге равен .
Решение.
Рассмотрим схему процесса волочения
(рис. 1.8). Кинематически допустимое
поле скоростей принято таким же, как
и при решении задач 1.4 и 1.5. Поэтому
выражение для
|
Рис.1.8 |
Мощность внешних сил при волочении
![]()
Поэтому остаются справедливыми и выражения (1.15) и (1.17) для верхней оценки удельного усилия волочения.
Для верхних оценок усилия и мощности волочения имеем
![]() .
.
Задача 1.9. Выполнить задание 1.1 с учетом трения на контактных границах инструмента и заготовки.
Задача 1.10. Выполнить задание 1.3 с учетом трения на контактных границах инструмента и заготовки.