14. Визначений інтеграл.

Визначений інтеграл - це число, яке знаходится за формулою Ньютона-Лейбніца: , де - первісна до функції .

Якщо при обчиленні визначеного інтеграла застосовують заміну змінної : , де - неперервна функція, що має похідну на відрізку , то використовується формула

, де .

При обчисленні визначеного інтеграла не потрібно повертатись до попередньої змінної.

При методі інтегрування частинами формула має вигляд:

.

Площа криволінійної трапеції, обмеженої кривою , віссю та прямими , обчислюється за формулою

Якщо криволінійна трапеція обмежена зверху лінією , знизу лінією , та прямими обчислюється за

формулою: .

Об’єм тіла обертання фігури обмеженої лініями: , , навколо осі знаходимо за формулою:

.

Якщо фігура, обмежена лініями: , , обертається навколо осі , то об’єм:

15. Невласні інтеграли.

За означенням невласні інтеграли з необмеженими межами:

, ,

.

Якщо ці границі скінченні, то невласні інтеграли називаються збіжними, якщо нескінченні або не існують, то розбіжні.

Якщо підінтегральна функція в точці необмежена і терпить розрив, то ;

Якщо необмежена в точці , то .

Якщо терпить розрив у внутрішній точці , то .

Інтеграл Пуассона: .

16. Диференціальні рівняння першого порядку.

Диференціальним рівнянням першого порядку називається рівняння вигляду , яке, коли його можна розв’язати відносно набуває вигляду або .

Функція , де - довільна стала, називається загальним розв’язком рівняння першого порорядку, якщо при підстановці її в рівняння, вона перетворює його в правильну рівність. Якщо цей розв’язок задає функцію неявно: , то знайдено загальний інтеграл. При довільному одержимо частковий розв’язок (частковий інтеграл).

Задача знаходження розв’язку , який задовільняє початкові умови при , називається задачею Коші для рівняння першого порядку.

Розглянемо деякі класи диференціальних рівнянь, які розв’язуються в квадратурах (розв’язки виражаються через інтеграли від заданих функцій).

Диференціальне рівняння вигляду називається рівнянням з відокремленими змінними . Його загальний інтеграл: .

Диференціальне рівняння вигляду називається рівнянням з відокремлюваними змінними.

В ньому змінні можна розділити і знайти загальний інтеграл

.

Зауваження. Часто для зручності спрощень записують у вигляді .

Лінійним дифрінянням першого порядку називається рівняння, яке містить шукану функцію , та її похідну в першому степені і не містить їх добутків: .

Підстановкою , за методом Бернулі воно приводиться до інтегрування двох дифрівнянь з відокремлюваними змінними.

Однорідним дифрівнянням першого порядку називається рівняння вигляду , де - однорідні функції одного виміру. Функція називається однорідною виміру , якщо .

Однорідне дифрівняння зводиться до рівняння вигляду .

Підстановкою воно зводиться до рівняння з відокремлюваними змінними.

17. Лінійні диференціальні рівняння другого порядку з постійними коефіцієнтами.

Лінійним диференціальним рівнянням другого порядку з постійними коефіцієнтами називається рівняння вигляду , де - сталі числа.

Відповідним характеристичним рівнянням називається рівняння:

.

Загальний розв’язок заданого дифрівняння залежить від коренів цього характеристичного рівняння.

1. Якщо корені характеристичного рівняння дійсні та різні, 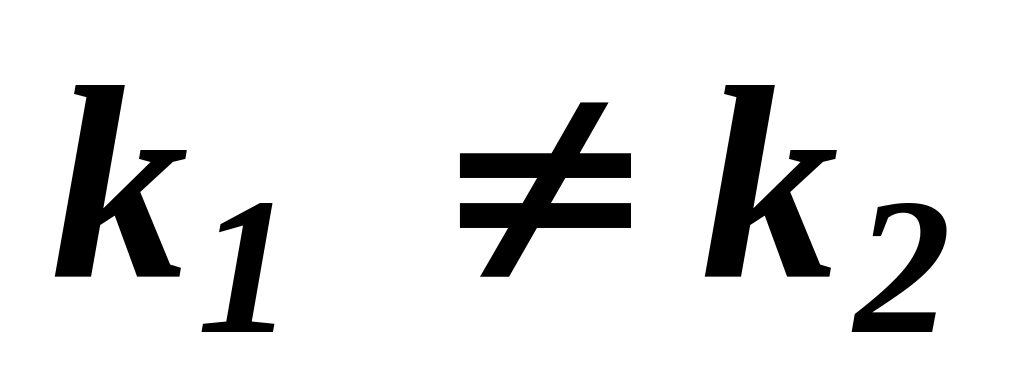, то загальний розв’язок дифрівняння має вигляд .

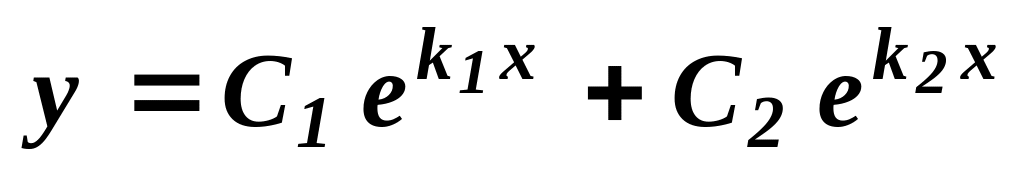2. Якщо корені характеристичного рівняння дійсні і рівні, тобто 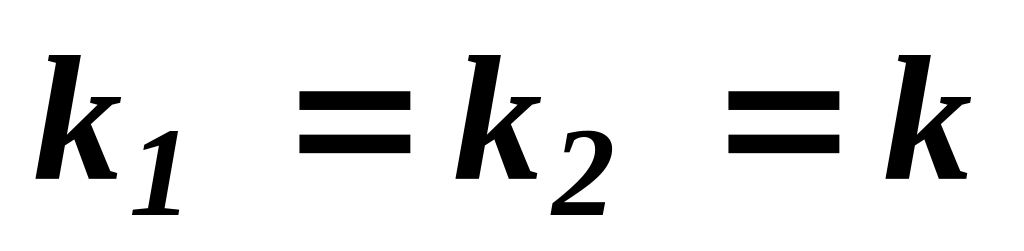, то загальний розв’язок .

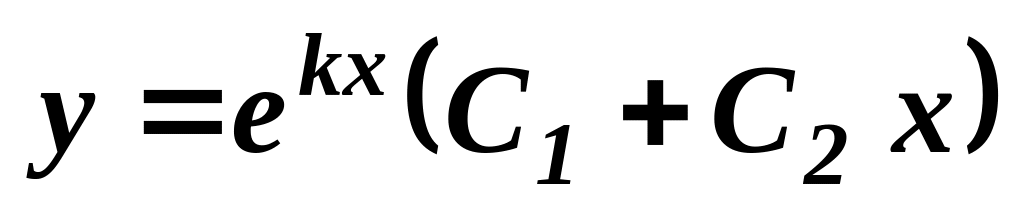3. Якщо корені характеристичного рівняння комплексно спряжені, тобто 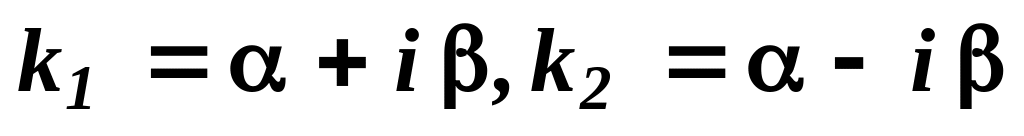,де , то загальний розв’язок .

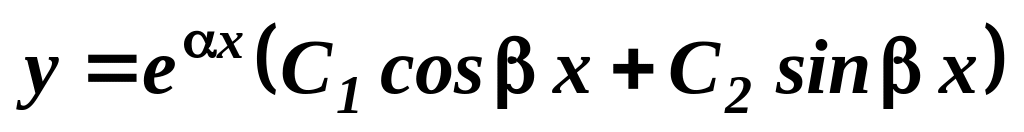Неоднорідне лінійне дифрівняння другого порядку з постійними коефіцієнтами має вигляд , де - сталі числа.

Загальний розв’язок лінійного дифрівняння ( ) дорівнює сумі загального розв’язку відповідного однорідного рівняння ( ) і довільного часткового розв’язку ( ) даного неоднорідного рівняння, тобто

Частковий розв’язок ( ) підбирається для деяких функцій подібним до неї.

1. Нехай , де многочлен 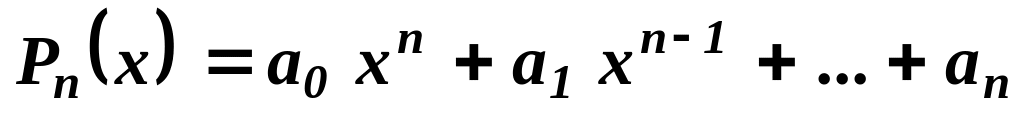. Тоді частковий розв’язок шукаємо у вигляді

якщо - не корінь характеристичного рівняння ;

, якщо - простий корінь характеристичного рівняння ;

, якщо - подвійний корінь характеристичного рівняння, де ,( -невідомі сталі коефіцієнти, які знаходяться методом невизначених коефіцієнтів).

2. Нехай 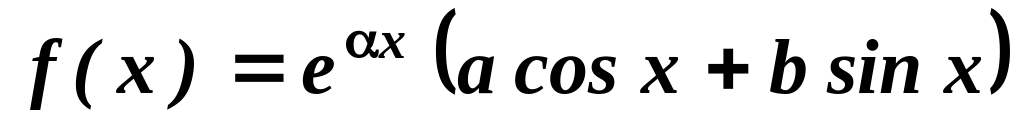, тоді частковий розв’язок

якщо - не корінь характеристичного рівняння ;

, якщо - корінь характеристичного рівняння ;

Для дифрівняння другого порядку загальний розв’язок містить дві довільні сталі. Задача Коші ставиться так:

Знайти такий розв’язок, який би задовільняє умови , при .