Короткі теоретичні відомості.

1. Визначники. Обчислення визначників.

Визначником 2-го порядку називається число, яке знаходиться за формулою:

В

a₁₁ a₂₂ a₃₃ + a₁₂ a₂₃ a₃₁ + a₂₁ a₃₂ a₁₃-

-a₁₃ a₂₂ a₃₁ – a₁₂ a₂₁ a₃₃ – a₁₁ a₂₃ a₃₂.

изначником 3-го порядку називається число, яке знаходиться за формулою:

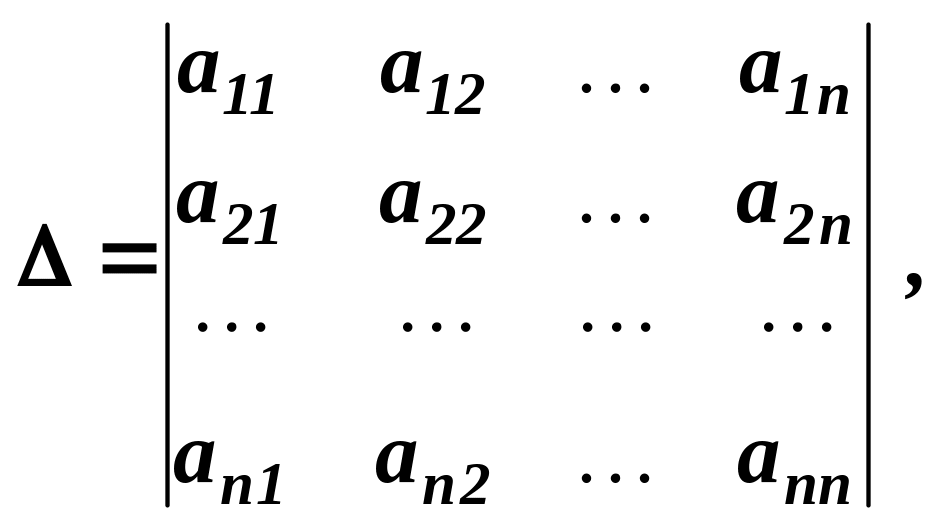
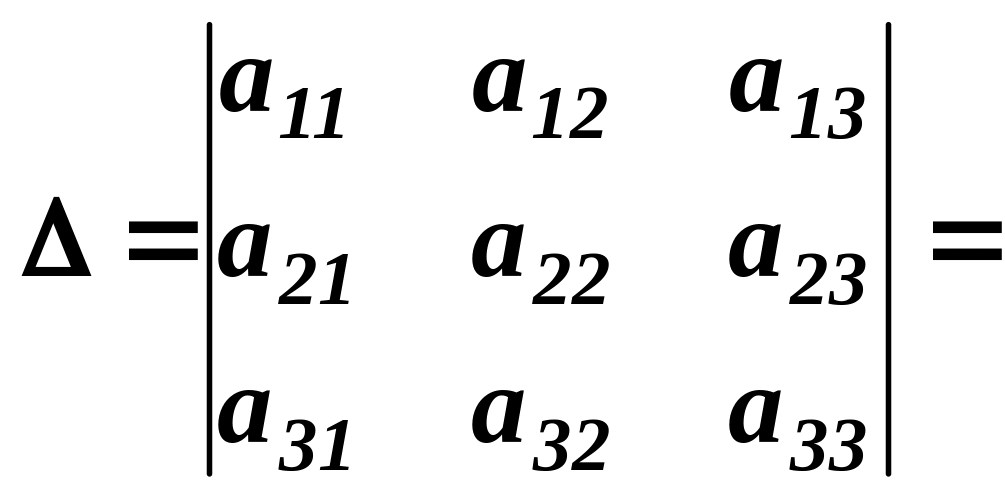
Визначник n-го порядку має вигляд:

де а_ij – елемент визначника, i – вказує стрічку розміщення, j – стовпець.

Мінором М_ij елемента а_ij визначника n-го порядку називається визначник (n-1)-го порядку, одержаний з попереднього викреслюванням i-го рядка і j-го стовпця.

Алгебраїчним доповненням А_ij елемента а_ij визначника n-го порядку називається мінор цього елемента, взятий із знаком “+”, якщо число (i+j) – парне і зі знаком “- ”, якщо воно непарне. A_{ij =} (-1)^i+jM_ij.

Визначник n-го порядку це число, яке дорівнює сумі попарних добутків елементів довільного рядка (або стовпця) на їх відповідні алгебраїчні доповнення.

2. Матриці та дії над ними.

Прямокутна таблиця чисел, що містить стрічок і стовпців, взята в круглі або в квадратні дужки називається матрицею розмірності

Якщо , то матриця називається квадратною порядку.

Сумою (різницею) матриць А і В однакової розмірності називається

матриця С, для якої кожний елемент дорівнює сумі (різниці) відпо-

відних елементів даних матриць:

Добутком матриці A на число k називається матриця kA, всі елементи якої дорівнюють добуткам відповідних елементів матриці A на це число. Матричне множення AB можливе, якщо число стовпців матриці A співпадає з числом рядків матриці B.

Добутком матриці A розмірності на матрицю В розмірності , називається матриця , розмірності , для якої кожний елемент знаходиться за формулою:

Для квадратної матриці існує обернена матриця відносно множення.

Схема знаходження оберненої матриці:

1 ) Обчислити визначник матриці А.

2) Транспонувати матрицю А. .

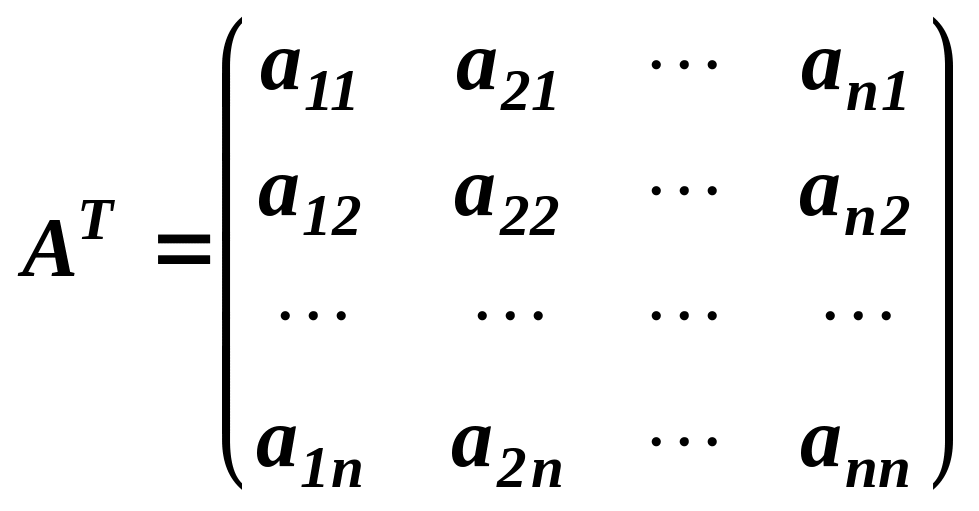3) Знайти алгебраїчні доповнення кожного елемента транспонованої матриці і записати їх у матрицю (приєднану):

= .

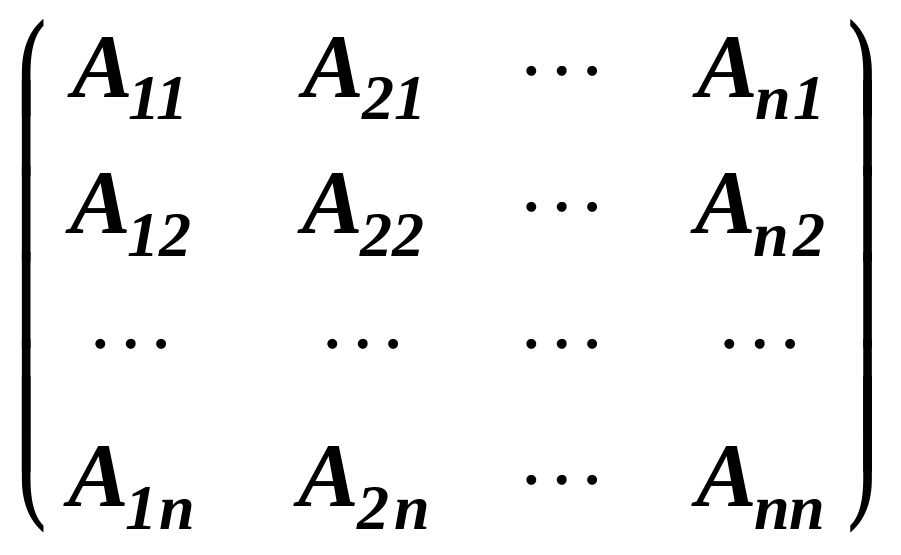4) Поділити кожен елемент матриці на визначник матриці |А|.

Рангом матриці А називається найвищий порядок відмінних від нуля мінорів. Його позначають буквою r (r (A)).

3. Розв'язування систем лінійних алгебраїчних рівнянь

Система лінійних алгебраїчних рівнянь має вигляд:

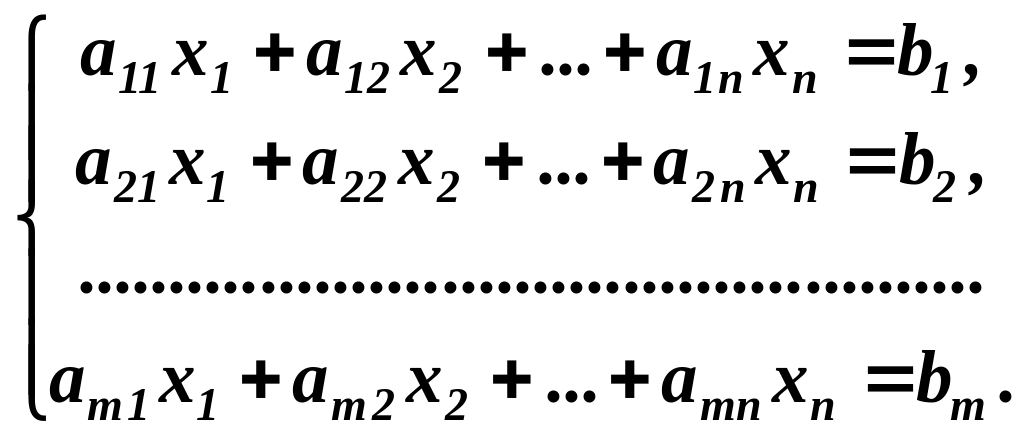(1)

Числа - коефіцієнти біля невідо-

мих , а - вільні члени.

Розв’язком системи (1) називається сукупність чисел яка при підстановці її в систему перетворює всі рівняння в правильні рівності (тотожності).

Якщо число рівнянь дорівнює числу невідомих то для розв’язування системи рівнянь можна використати:

а) правило Крамера. Якщо основний визначник системи лінійних алгебраїчних рівнянь з невідомими ( визначник складений із коефіцієнтів, що стоять біля невідомих) не дорівнює нулю, то ця система має єдиний розв’язок, який знаходиться за формулами:

де -допоміжний визначник, який одержується з основного визначника шляхом заміни його стовпчика стовпчиком вільних членів системи.

б) матричний метод. У матричній формі систему лінійних рівнянь запишемо так . Звідси розв’язок: .

Для довільних систем, лінійних алгебраїчних рівнянь використовують методи Гаусса, Жордана –Гаусса.

в) метод Гаусса полягає в послідовному виключенні невідомих з рівнянь системи і зведенні її до трикутного чи трапецевидного вигляду.

г) метод Жордана - Гаусса полягає в повному послідовному виключенні невідомих. При цьому коефіцієнти утворять при основних (базисних) невідомих одиничну матрицю.

4. Елементи аналітичної геометрії і векторної алгебри.

Дві взаємно перпендикулярні осі Ох і Оу з спільною точкою початку відліку О і однаковою масштабною одиницею утворюють декартову систему координат на площині.

Точка на площині задається впорядкованою парою чисел (х,у), які називають координатами.

Віддаль d між точками А( x₁, y₁) і B( x₂, y₂) обчислюється за формулою: d = .

Координати точки С (x, y), яка ділить відрізок АВ у відношенні АССВ=, знаходяться за формулами: .

В просторі три взаємно перпендикулярні осі Ох,Оу,Оz з спільною точкою відліку О і однаковою масштабною одиницею утворюють декартову систему координат.Точка в просторі задається впорядкованою трійкою чисел ­­– координатами (х,у,z).

Направлений відрізок , де точка А точка початку,а В точка кінця називається вектором.

Вектор позначається або двома великими буквами з стрілкою над ними ,або одною малою буквою . Довжину вектора називають модулем і позначають або .

Вектор на площині задають двома числами його координатами: ,де , , які є проекціями вектора відповідно на осі Ох та Оу.Вектор в просторі задають трьома координатами: .

Сумою(різницею) двох векторів і називають вектор .

Скалярним добутком векторів і називають вектор , де - кут між векторами.

Якщо вектори задані своїми координатами, то

Кут між векторами обчислюється за формулою:

cos =

Умова паралельності векторів: .

Умова перпендикулярності векторів:

5. Пряма на площині

1. Рівняння прямої з кутовим коефіцієнтом: y = kx + b, де ( - кут нахилу прямої до додатнього напряму осі , b - довжина відрізка, який пряма відтинає на осі Oy.

2. Рівняння в’язки прямих, що проходять через точку

3. Рівняння прямої, що проходить через дві точки

4. Рівняння прямої у відрізках на осях: де - відрізки, які пряма відсікає на осях координат.

5.Загальне рівняння прямої: Ax + By + C = 0.

Кут , відрахований проти годинникової стрілки від прямої

до прямої знаходиться за формулою:

.

Умова паралельності цих прямих :

Умова перпендикулярності:

Віддаль точки від прямої обчислюємо за формулою: