Принцип д'Аламбера для механической системы

Рассмотрим материальную точку массой т_k системы, состоящей из N точек. Обозначим ускорение этой точки a_k, равнодействующую внешних сил через , равнодействующую внутренних сил, приложенных к той же точке через . Реакции связей входят в . Тогда принцип Д'Аламбера будет иметь вид

,

где .

Складывая почленно полученные уравнения для всех N точек, получим

k = l,2,...,N.

В этом уравнении первая сумма равна главному вектору внешних сил, приложенных к системе; вторая сумма равна нулю, поскольку геометрическая сумма всех внутренних сил системы равна нулю; последняя - главному вектору сил инерции. Таким образом,

,

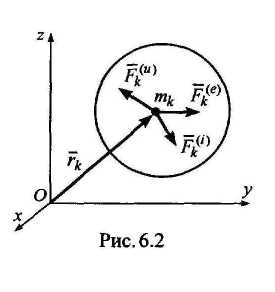
т.е. в каждый момент времени сумма главных векторов внешних сил и сил инерции движущейся системы равна нулю.

Выберем произвольный полюс О и проведем из него к точке т_к радиус-вектор . Умножая каждое слагаемое принципа Д'Аламбера векторно на соответствующий радиус-вектор слева и складывая все N полученных таким образом уравнений, имеем

, k = l,2,...,N

Первая сумма равна главному моменту внешних сил, приложенных к системе; вторая сумма равна нулю, а последняя -главному моменту сил инерции. Следовательно,

,

т.е. в каждый момент времени сумма главных моментов внешних сил и сип инерции движущейся механической системы равна нулю.

Двум векторным уравнениям соответствуют шесть уравнений в проекциях на оси декартовых координат

, ,

, ,

Движение твердого тела, как частный случай механической системы, вполне определяется этими шестью уравнениями. Если рассматривается система, состоящая из нескольких тел, то можно составить соответствующие уравнения для каждого тела в отдельности.

Главный вектор сил инерции механической системы

Вычислим главный вектор сил инерции. Имеем

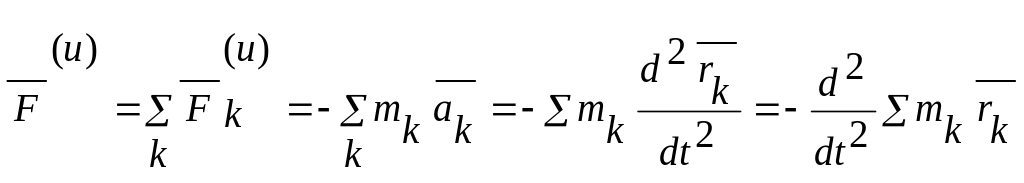
Сумма , где r_c - радиус-вектор центра масс системы, следовательно,

,

т.е. главный вектор сил инерции системы равен произведению массы всей системы на ускорение центра масс, приложен в точку центра масс и направлен противоположно вектору а_с.

Главный вектор сил инерции твердого тела

Твердое тело является частным случаем механической системы. Следовательно, главный вектор сил инерции твердого тела находится также как и для механической системы.

Тогда проекции главного вектора на декартовые оси координат имеют вид

, , ,

здесь х_с, y_c, z_c - координаты центра масс тела.

Если тело движется прямолинейно по си х, то

, , .

Главный момент сил инерции механической системы

Вычислим главный момент сил инерции системы.

Имеем

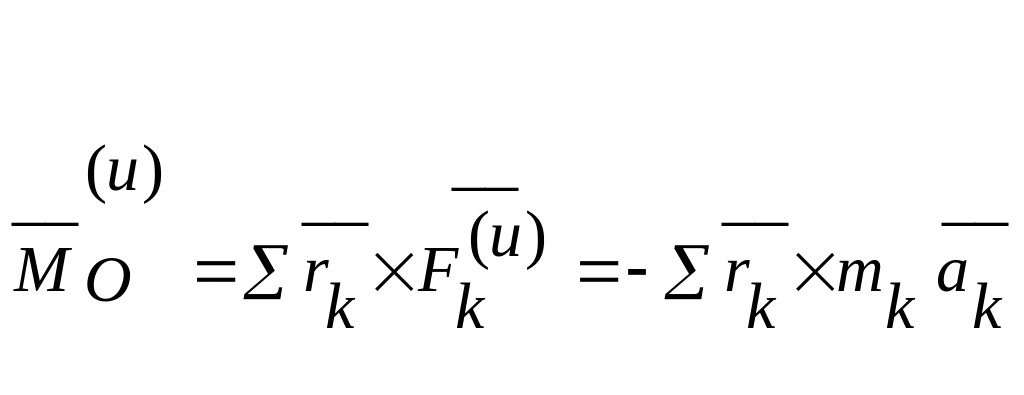, k = 1,2,..,N;

так как , преобразуем правую часть

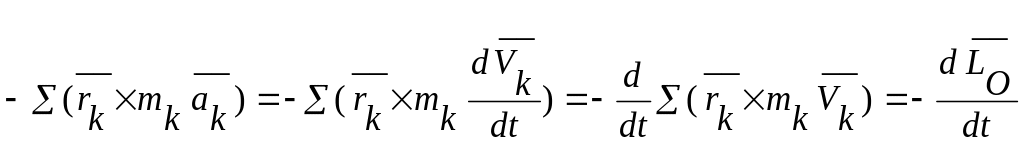
Здесь - кинетический момент системы.

Подставляя полученное выражение в теорему об изменении кинетического момента, получаем значение главного момента сил инерции

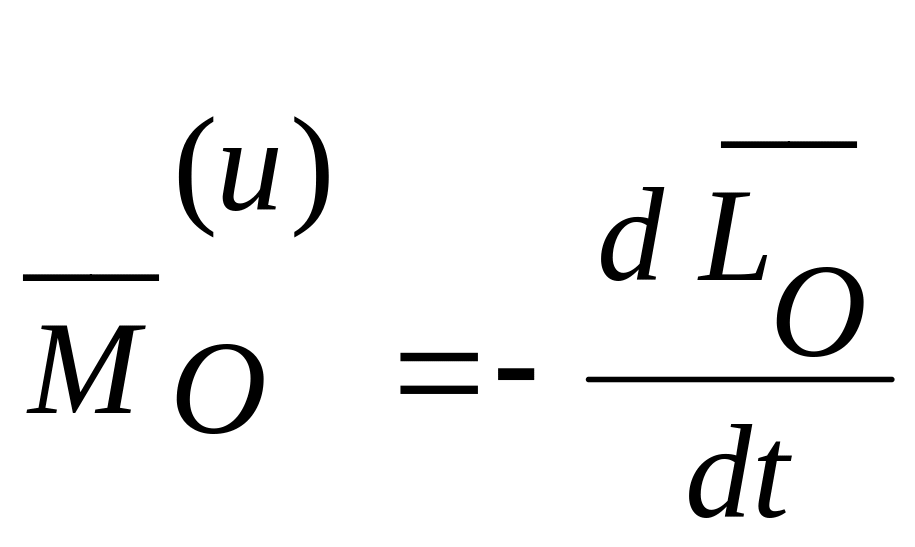
Главный момент сил инерции твердого тела, вращающегося вокруг неподвижной оси

В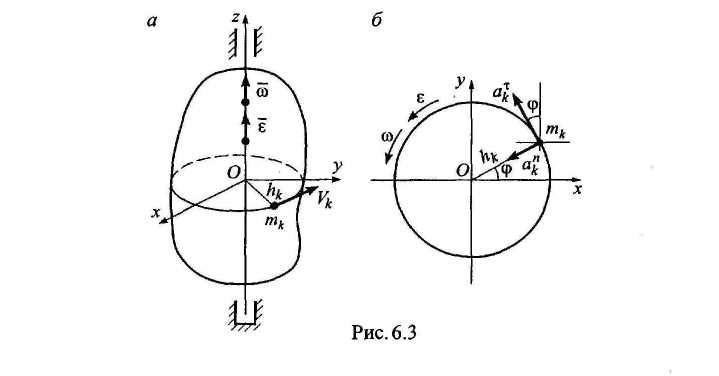 ычислим координаты главного момента сил инерции твердого тела, вращающегося вокруг неподвижной оси. Ось Oz совместим с осью вращения, а оси Ох и Оу скрепим с вращающимся телом, тогда (0,0,ε) и (0,0,ω), r_k(x_k;y_k;z_k) - радиус-вектор рассматриваемой точки т_к. При вращении тела вокруг неподвижной оси Oz ускорение любой точки т_к состоит из нормального ускорения и касательного ускорения , где h_k - расстояние точки k от оси вращения Oz:

;

;

.

Здесь учтено, что h_kcosφ = x_k , h_ksinφ = у_к, х_к и у_к - координаты точки т_к.

Тогда, согласно (6.12), получим,

Здесь J_xz, J_yz - центробежные моменты инерции, J_z - осевой момент инерции.

Таким образом, главный момент сил инерции твердого тела, вращающегося вокруг неподвижной оси, сводится к паре сил, момент которой равен

где

, ,

Если ось вращения проходит через центр тяжести тела и оси Oxyz являются главными осями, то

, ,

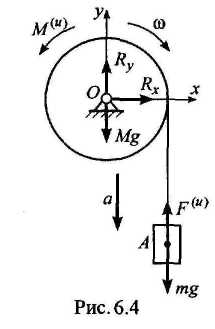Пример 3. Через блок весом Mg и радиу­сом R перекинута нерастяжимая нить, на конце которой подвешен груз А весом mg. Определить ускорение а груза А, натяжение нити Т и давление на подшипник оси блока.

Решение. Пусть груз А опускается вниз, тогда сила инерции груза вверх: F^и = ma.

Поскольку ось вращения диска является осью симметрии, то J_xz=J_yz = 0. Следовательно, момент от сил инерции, равен и направлен в сторону противоположную вращению диска.

Отбросим опору О, заменим ее действие реакциями подшипника R_x и R_y. Составим уравнения кинетостатики:

, ;

, ;

, .

Подставим в последнее уравнение значения силы инерции F^(u)=ma и момента от сил инерции = (J/R)a, где t = a/R, и решим его относительно ускорения а.

Получим

, .

Тогда из первых двух уравнений (а) определим

,

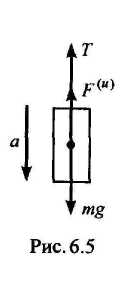
Для определения натяжения нити разорвем гибкую связь и заменим ее действие натяжением Т. Добавляя внешнюю силу mg и силу инерции F^(и), имеем

-mg+F^(u)+T = 0,

откуда T = mg- F^(и) = m(g - а) = .

Если считать диск сплошным телом, то J_z - —mR², тогда

, , , .

Лекция 16 (Аналитическая механика)

«Связи и их классификация. Обобщенные координаты,

Работа силы на возможном перемещении»

В основу классической механики положены понятия пространства, времени, силы и массы. Она оперирует векторными величинами, векторными уравнениями и их проекциями на координатные оси. Аналитическая механика построена на основных принципах, основанных на сравнении движений. Этот принцип изучает мгновенное состояние движения и возможные отклонения от этого состояния, допускаемые связям в данный момент времени. В аналитической механике широко применяются скалярные меры движении материальных объектов и меры их действия (кинетическая энергия, работа сил и т.д.).

Основы изложения аналитической механики составляют некоторые общие принципы, из которых аналитическим путем получаются дифференциальные законы движения на основе которых изучается движение твердых тел и системы материальных точек.