Способы нахождения мгновенного центра ускорений.

1 .

Ускорения всех точек направлены к мгновенному центру ускорений, так как они состоят только из одной нормальной составляющей от вращения вокруг мгновенного центра ускорений. Если известно a_A, то AQ=a_A/².

2 .

(мгновенное поступательное движение)

Мгновенный центр ускорений лежит на пересечении перпендикуляров к ускорениям точек. Если известно a_A, то AQ=a_A/

3.

И меем общий случай, ранее уже обсуждавшийся. Угол  откладываем по дуговой стрелке  от вектора ускорения.

Если известно a_A, то

1. Пусть в данный момент времени известны ускорения двух точек плоской фигуры A и B. Приняв за полюс точку A, имеем:

(*)

где

Проецируя левую и правую части векторной формулы (*) на оси Bx и BY получаем:

Здесь  и  в принципе известные углы.

Проекцию aⁿ_BA на ось Вх берем со знаком (+), так как она всегда направлена к оси вращения. Проекцию a^_BA, берем со знаком (+) предполагая, что стрелка  направлена против часовой стрелки.

Из уравнений проекций находим

знак  определяется после подстановки данных в формулу.

После того, как найдены  и , задача нахождения мгновенного центра ускорений сводится к случаю 3.

Вычисление углового ускорения при плоском движении.

1. Если известен угол поворота фигуры как функция времени, то

2. Находим мгновенный центр скоростей и, зная скорость некоторой точки А, находим угловую скорость  вращения фигуры

если AP – const, то

Пример.

К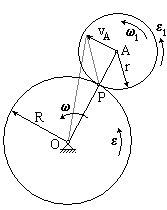 ривошип OA вращается с угловой скоростью  и угловым ускорением  вокруг центра О. Колесо радиуса r катится без скольжения по колесу радиуса R. Найдем угловую скорость и угловое ускорение вращения колеса радиуса r.

Мгновенным центром скоростей подвижного колеса является точка P. Тогда ₁ = v_A/AP = v_A/r. Но в то же время точка А совершает вращение вокруг точки О с угловой скоростью .

 = v_A/AO = v_A/(r + R)

Отсюда получаем

При внутреннем зацеплении колес дуговые стрелки  и  колеса и кривошипа имеют потивоположные направления.

3. Иногда угловое ускорение  плоской фигуры можно найти путем проецирования на оси координат известного по направлению ускорения (например, точки В), если ускорение какой-либо другой точки А и угловая скорость фигуры  известны или их можно вычислить предварительно.

При этом используем формулу и проецирование ведем на ось, перпендикулярную a_B.

Пример.

Кривошип OC приводит в движение линейку эллипсографа AB, один конец которой с помощью ползуна В удерживается на оси y, другой конец A – на оси x. Ускорение точки В направлено вдоль оси y. Рассмотрим проекцию вышеприведенной формулы на ось x:

Этот метод подходит для шатунов, у которых есть точка, которая движется прямолинейно.

Если же известны ускорения двух точек А и В по модулю и направлению, то мы имеем случай 4 для нахождения мгновенного центра ускорений (проецируем формулу для связи ускорений на направление АВ и перпендикулярное ему).

4. В задачах, где можно определить тождественное соотношение между углами поворота, проводим двойное дифференцирование. В ранее рассмотренном примере для мгновенного центра скоростей мы получили .

Дифференцируя вторично, будем иметь

Если d/dt=-const, то

Лекция 9 (динамика)

«Классификация сил, динамика материальной точки. Основные виды прямолинейного движения точки. Криволинейное движение»