Вычисление угловой скорости при плоском движении.

Угловую скорость плоской фигуры при плоском движении можно вычислить, согласно определению, как

Также ее можно определить так:

Величину  можно вычислить путем предварительного нахождения скорости какой-либо точки плоской фигуры от вращения фигуры вокруг другой ее точки, принятой за полюс: , знак угловой скорости определяют по направлению относительной скорости.

Еще один способ такой: если предварительно установить зависимость угла поворота плоской фигуры от линейных угловых величин других плоских фигур тождественным соотношением, то дифференцируя его по времени, получаем соотношение, из которого иногда удается определить искомую угловую скорость.

Пример. В несимметричном (смещенном) кривошипно-шатунном механизме установить зависимость между угловыми скоростями кривошипа OA -  и шатуна AB - 1: Для </2 r Sin + h = l Sin После дифференцирования Учитывая, что , получаем: (при h=0 и r=l  = 1)

Ускорения точек при плоском движении. Мгновенный центр ускорений.

За переносное движение тела примем поступательное движение, за относительное движение – вращение тела вокруг полюса А.

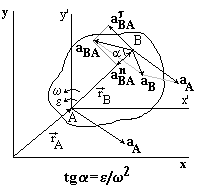Полюс А движется с ускорением a_A и тело вращается вокруг полюса с угловой скоростью  и угловым ускорением . Из формул для сложного движения точки имеем:

Эту формулу можно представить в виде:

Ускорение a_BA точка В получает из-за вращения вокруг полюса А, компоненты этого ускорения определяются так:

отсюда

Мгновенный центр ускорений. В каждый момент движения плоской фигуры в своей плоскости, если  и  не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно нулю. Эту точку называют мгновенным центром ускорений, мы будем ее обозначать Q.

Пусть нам известны по модулю и направлению ускорение какой-либо точки плоской фигуры (точка О), угловая скорость и угловое ускорение  этой фигуры.

Мгновенный центр ускорений лежит на прямой, проведенной под углом  (tg=/²) к ускорению точки О. При этом  надо отложить от ускорения a_O в направлении дуговой стрелки углового ускорения .

Только в точках этой прямой ускорение a_O и ускорение от вращения a_QO могут иметь противоположные направления и одинаковые по модулю значения.

Но , следовательно .

Мгновенный центр ускорений является единственной точкой фигуры, ускорение которой в рассматриваемый момент времени равно нулю. В другой момент времени мгновенный центр ускорений находится в общем случае в другой точке плоской фигуры.

Если положение мгновенного центра ускорений известно, то выбрав его за полюс, для ускорения произвольной точки А имеем :

и ускорение a_A направлено под углом  к отрезку AQ, соединяющего точки A и Q в сторону дуговой стрелки .

Ускорения двух точек A и B показаны на рисунке, их величины равны

Итог: ускорения точек плоской фигуры при плоском движении можно определить также, как и при вращательном движении плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью  и угловым ускорением .

Для вычисления скоростей принимают, что фигура вращается вокруг мгновенного центра скоростей, для вычисления ускорений принимают, что фигура вращается вокруг мгновенного центра ускорений. В общем случае эти центры являются разными точками плоской фигуры.

Ускорения точек плоской фигуры при плоском движении подобно скоростям точек можно вычислить двумя способами: по формуле , выражающей зависимость ускорений двух точек плоской фигуры (способ 1) и по формуле , используя мгновенный центр ускорений (способ 2). Часто мгновенный центр ускорений (кроме случаев  или  равных нулю) располагается так, что трудно определить расстояние от него до рассматриваемых точек фигуры, поэтому рекомендуется использовать способ 1 через формулу, связывающую ускорения точек фигуры.