Проверочная работа № 5–0

(с решением)

1. Написать уравнение касательной и нормали к кривой

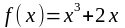в точке с абсциссой x_о= 1 .

2. Вычислить приближенно .

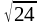3. Проверить, является ли функция

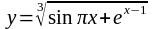
эластичной в точке x_о= 1.

4. Найти пределы, используя правило Лопиталя:

а) 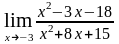; б) .

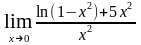5. Найти промежутки монотонности функции:

.

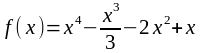6. Найти промежутки монотонности функции:

.

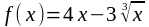7. Найти экстремумы функции:

.

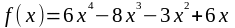8. Исследовать методами дифференциального

исчисления функцию 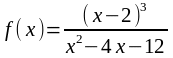и

построить график.

Решение проверочной работы № 50.

1. Для определения углового коэффициента касательной находим

производную заданной функции:

.

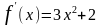Значение производной в точке с абсциссой x_о= 1 даёт искомый

угловой коэффициент

.

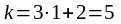Значение функции в точке x_о= 1:

.

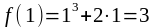Воспользовавшись уравнением

,

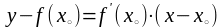получим уравнение касательной:

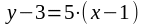или ,

а уравнение нормали получим, используя уравнение

.

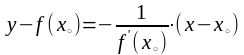Таким образом, уравнение нормали имеет вид:

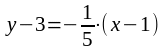или .

Ответ: - уравнение касательной,

- уравнение нормали.

2. Воспользуемся приближённой формулой

.

Учитывая, что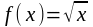 , x_о= 25, 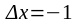, получим

,

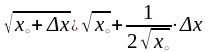т.е.

.

Ответ: .

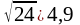3. Найдём коэффициент эластичности данной функции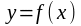 по

формуле

.

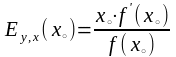Имеем

.

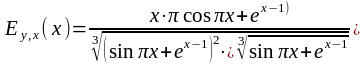Так как 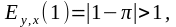то данная функция является эластичной

в точке x_о= 1.

Ответ: функция является эластичной в

точке x_о= 1.

4 а). Поскольку и ,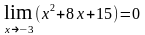

то в данном случае имеем неопределённость вида .

Воспользуемся правилом Лопиталя:

.

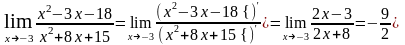4 б). Здесь также имеет место неопределённость вида , так как

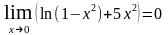и .

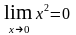Применяем правило Лопиталя:

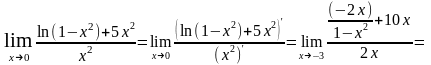
Ответ: 4 а)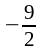 ; 4 б) 4.

5. Данная функция определена на всей числовой прямой, т.е. D(f) = R, а её производная равна

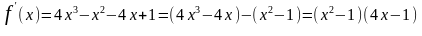
Производная обращается в нуль в трёх точках х = -1, х = , х =1.

Эти точки разбивают область определения функции на четыре промежутка (-¥,-1), (-1, ), ( ,1) и (1, +¥), в каждом из которых производная f'(x)сохраняет знак.

Подставим в выражение для f'(x) значения х = -2, х = 0, х = , х = 2 из указанных промежутков, тогда:

на (-¥,-1) имеем f'(-2)< 0;

на (-1, ) имеем f'(0)> 0;

на ( , 1) имеем f'( )< 0;

на (1, +¥) имеем f'(2) >0.

Следовательно, в промежутках (-¥,-1) и( ,1) функция убывает, а в промежутках

(-1, ) и (1, +¥) – возрастает.

6. Функция определена и дифференцируема на всей числовой прямой, причём

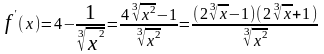
Производная обращается в нуль в точках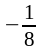: х = , х =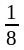 и не существует в точке х = 0.

Эти три точки делят область определения на четыре промежутка

(-¥, ), ( , 0), (0, ) и ( , +¥).

Определим знак производной в каждом из них

на (-¥, ) имеем f'(-1) > 0;

на ( , 0) имеем f'(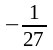 )< 0;

на (0, ) имеем f'(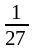 )< 0;

на ( , +¥) имеем f'(1) >0.

Таким образом, в промежутках (-¥, )и ( , +¥) функция возрастает, а в промежутке ( , ) – убывает.

7. Область определения функции D(f) = R. Дифференцируя данную функцию, находим

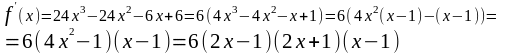
Производная обращается в нуль при х = , х = и х =1. Эти точки разбивают числовую ось на четыре промежутка(-¥, ), ( , ), ( ,1) и (1,+¥), внутри которых производная сохраняет определённый знак. Найдём знак производной в каждом из указанных промежутков:

на (-¥, ) имеем f'(-1) < 0;

на ( , ) имеем f'(0) > 0;

на ( ,1) имеем f'( )< 0;

на (1, +¥) имеем f'(2) >0.

Отсюда следует, что точки х = , х = и х = 1 являются экстремальными, так как при переходе через каждую из них производная меняет свой знак. При этом в точках х = и х = 1 происходит смена знаков с минуса на плюс, т.е. это - точки минимума; при переходе через точку х = знак производной меняется с плюса на минус, значит, это - точка максимума.

Найдем экстремумы функции, вычислив её значения в экстремальных точках:

f_min = f ( ) = 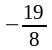, f_max = f ( ) = 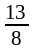, f_min = f (1) = 1.

8. Представим функцию в виде: .

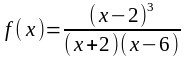Область определения функции D ( f ) – вся числовая прямая,

за исключением точек х = -2 и х = 6, т.е.

.

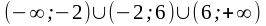Функция непериодическая; исследуем её на четность,

нечетность

,

.

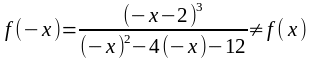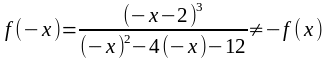Следовательно, данная функция не является ни чётной,

ни нечётной.

Найдём точки пересечения графика с осями

координат:

с осью Оу график пересекается при х = 0, при этом

у = f (0) = ,

т.е. М (0; ) - точка пересечения с осью Оу;

с осью Ох график пересекается в точках, в которых

f (х) = 0, т.е.

,

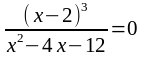откуда х = 2.

Таким образом, М (2; 0) - точка пересечения с осью Ох.

Находим интервалы знакопостоянства функции:

f (х) > 0 ,

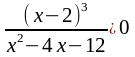
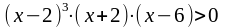т.е. при .

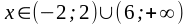Аналогично f (х) < 0 при .

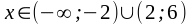Так как

,

,

,

,

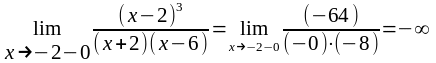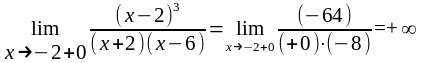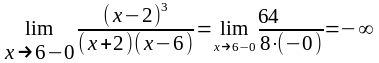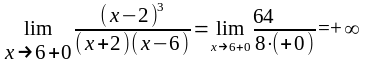то х = -2 и х = 6 являются точками разрыва второго рода,

а прямые х = -2 и х = 6 - вертикальными асимптотами.

Поскольку

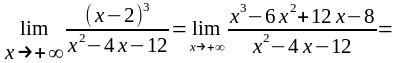
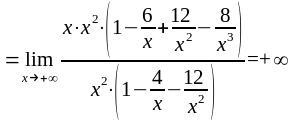, а ,

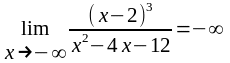то горизонтальных асимптот график функции не имеет.

Наклонная асимптота задаётся уравнением 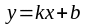, где

,

,

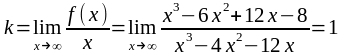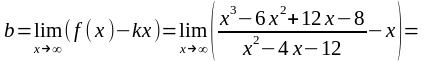
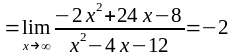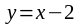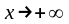т.е. прямая - наклонная асимптота при и при .

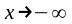Найдём интервалы монотонности и экстремумы функции, исследуя первую производную:

.

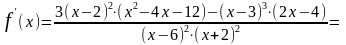
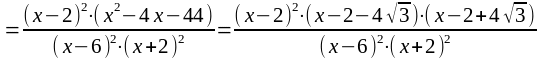Воспользуемся методом интервалов для исследования знака производной ( см. рис.1):

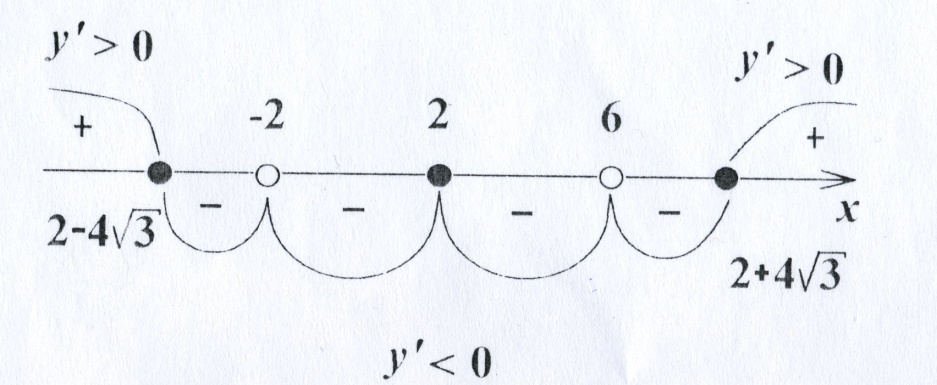
Рис.1

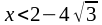При и при 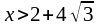производная 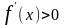, следовательно, функция возрастает.

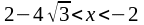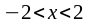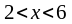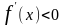При , , и производная , следовательно, функция убывает.

При переходе через точку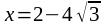 , производная меняет знак с «+» на «-», значит это точка локального максимума.

При переходе через точку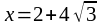 , производная меняет знак с «-» на «+», значит это точка локального минимума.

При переходе через точку х = 2, производная знака не меняет, значит в этой точке функция экстремумов не имеет.

Чтобы определить интервалы выпуклости и точки перегиба, вычислим вторую производную:

.

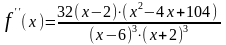Применим метод интервалов для исследования знака второй производной ( см. рис. 2):

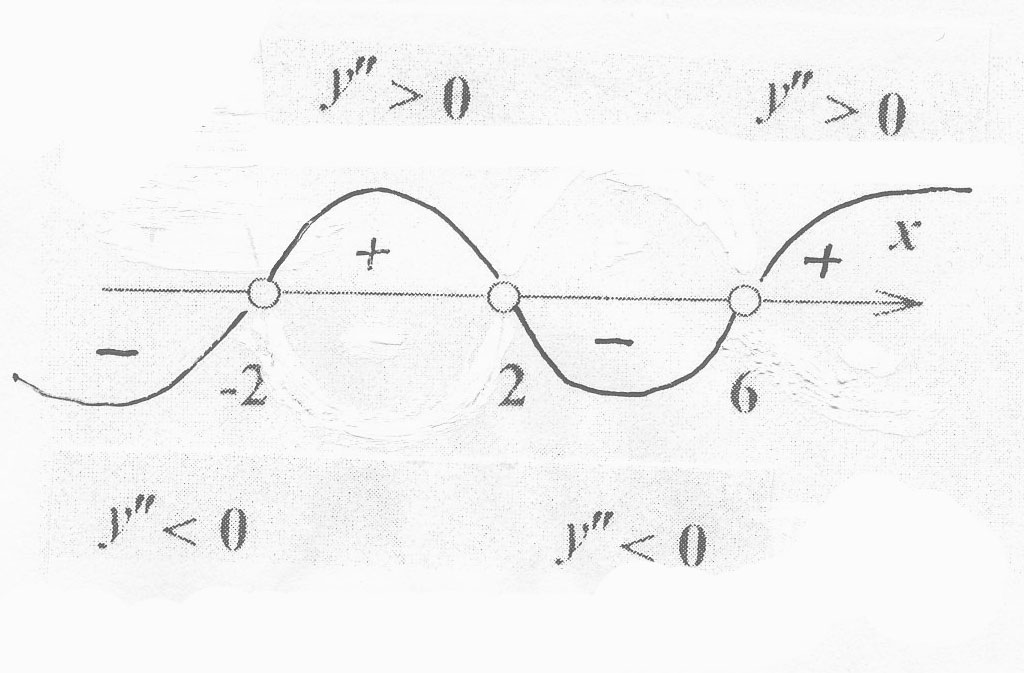
Рис. 2

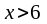
При и 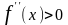, следовательно, функция выпукла вниз,

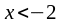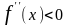При и , следовательно, функция выпукла вверх.

Учитывая всю полученную информацию о функции, строим график:

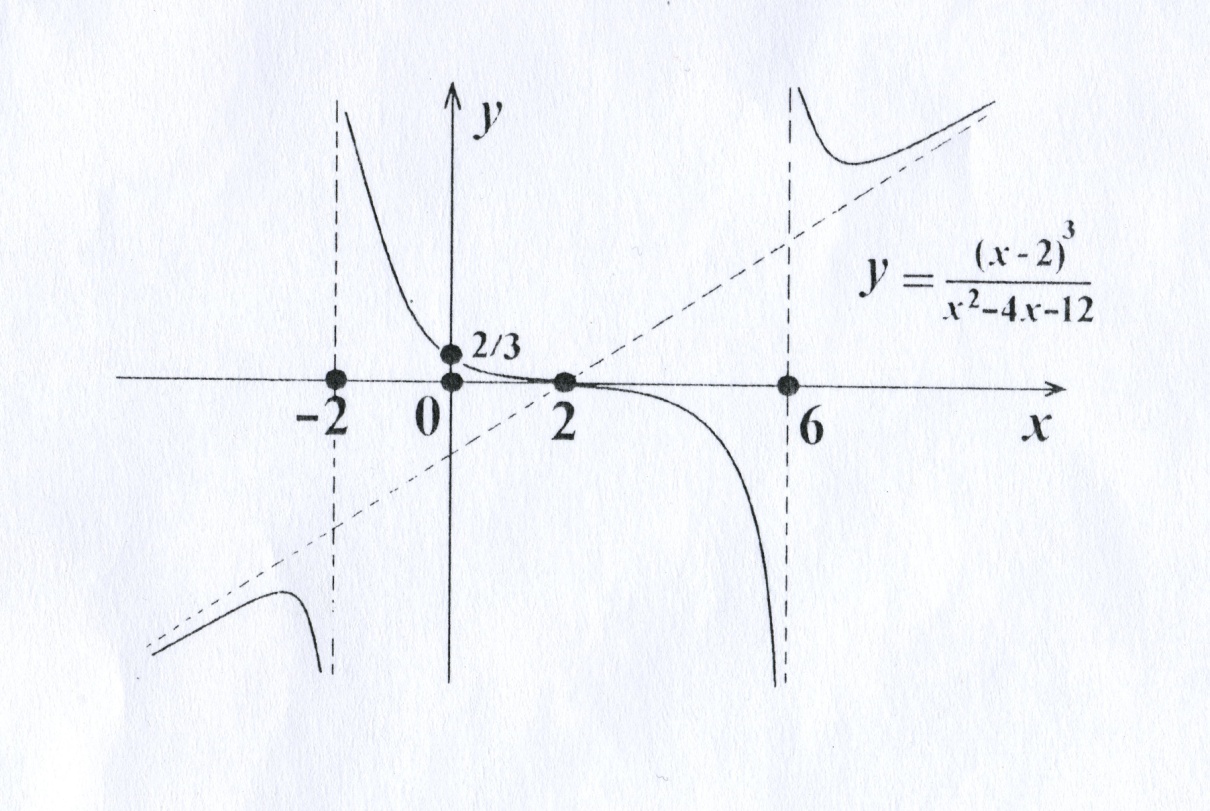
Рис. 3