
Проверочная работа №2– 0 (с решением)
1. Пользуясь определением предела
последовательности, доказать, что
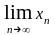 =
а, если:
=
а, если:
а) хn =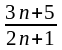 ,
а =
,
а = ;
б) хn =
;
б) хn =
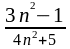 ,
а =
,
а = .
Указать номер
.
Указать номер
 .
.
2. Найти предел числовой последовательности.
а)
 ;
б)
;
б)
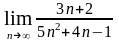 ;
;
в)
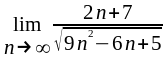 ;
г)
;
г)
 ;
д)
;
д)
 .
.
Решение проверочной работы №2– 0.
1.а) Найдём | хn
–
|
= |
–
|
= | |
= |
|
= |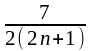 |
=
.
Определим, при каком значении n
выполняется неравенство
<
.
Так как 2( 2n + 1)
|
=
.
Определим, при каком значении n
выполняется неравенство
<
.
Так как 2( 2n + 1) 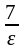 ,
то 4n + 2 >
или 4n >
–
2, откуда n >
,
то 4n + 2 >
или 4n >
–
2, откуда n > .
Поэтому за
возьмём целую часть числа
.
.
Поэтому за
возьмём целую часть числа
.
Таким образом, для любого 0 найдено такое число = [ ], что при всех n > выполняется неравенство | хn – | < , откуда по определению следует, что
 =
.
=
.
2.б) Задав произвольное положительное , решим неравенство | хn – | < , т.е.
|
–
| = |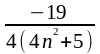 |
=
|
=
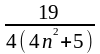 <
,
<
,
откуда находим 4(4n2
+ 5) > ,
или n >
,
или n >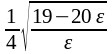 .
.
Полагая = [ ], получаем, что при n > выполняется неравенство | хn– | < , т.е. число по определению является пределом данной последовательности.
Ответ. 1.а) = [ ]; 2.б) = [ ].
2. а) Преобразуем выражение
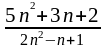 ,
поделив почленно числитель и знаменатель
на n2:
,
поделив почленно числитель и знаменатель
на n2:
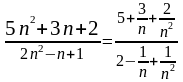 .
Так как
.
Так как =
=
 и
и
 =
=
 ,
то
,
то
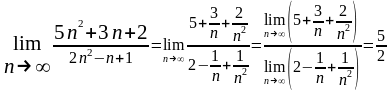 .
.
б) Разделив числитель и знаменатель на n2 , применяя теорему о пределе частного и теорему о пределе суммы (разности), получим
=
 =
=
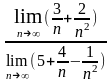 =
=
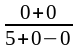 =
0.
=
0.
в) Разделим числитель и знаменатель на
n, внесем в знаменателе
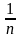 под знак квадратного корня и преобразуем
подкоренное выражение:
под знак квадратного корня и преобразуем
подкоренное выражение:
 .
.
Перейдя к пределу, получим =
 .
.
г)
=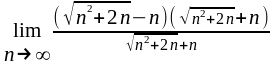 =
=
=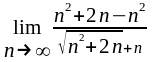 =
= =
= =1.
=1.
д) Упростим выражение
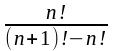 .
.
Так как
n! = 1· 2 ·3 ·…· n,
(n + 1)! = 1· 2· 3· …· (n + 1),
очевидно, что
(n + 1)! = n! · (n + 1)
и
= =
=
 =
=
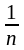 .
.
Следовательно,
=
 .
.
Ответ. 2. а)
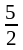 ;
2. б) 0; 2. в)
;
2. б) 0; 2. в)
 ;
2. г) 1; 2. д) 0.
;
2. г) 1; 2. д) 0.
Проверочная работа № 3 – 0
(с решением)
1. Используя ( - ) определение предела функции в точке, доказать, что
а)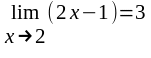 ; б)
; б)
 ;
в)
;
в)
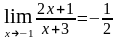 .
Указать ().
.
Указать ().
2.
Найти предел функции: а)
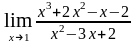 ;
б)
;
б)
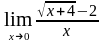 ; в)
; в)
 ;
;
г)
 ;
д)
;
д)
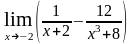 ;
е)
;
е)
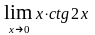 ;
;
ж)
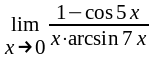 ;
з)
;
з)
 .
.
3. Найти предел функции, заменяя бесконечно малые эквивалентными:
а)
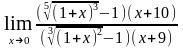 ;
б)
;
б)
 .
.
Решение проверочной работы № 3– 0.
1.а) f (x) = 2x – 1, b = 3. Нам надо доказать, что для всякого сколь угодно малого положительного числа существует такое число , зависящее от , > 0, что из неравенства 0 < | x – 2 | < следует неравенство | f (x) – 3 | < .
Зададим > 0 и составим выражение
| f (x) – 3 | = | (2x – 1) – 3 | = 2 | x – 2 |.
Если взять
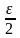 ,
то для всех значений х, удовлетворяющих
неравенству 0 < | x –
2 | < ,
,
то для всех значений х, удовлетворяющих
неравенству 0 < | x –
2 | < ,
| f (x) – 3 | = 2 | x – 2 |< 2 2 · = .Следовательно, по определению .
1.б) Пусть - любое положительное число. Требуется доказать, что можно подобрать такое число, зависящее от , > 0, что для всех х, удовлетворяющих неравенству 0 < | x – 2 | < , будет выполняться неравенство
| x2 – 4 | < .
Если |x–2|<, то |x+2|=|x–2+4| | x – 2 | + 4 < + 4 и | x2 – 4 | = | x – 2 | | x + 2 |< ( + 4).
Для выполнения неравенства | x2 – 4 | < достаточно потребовать, чтобы ( + 4) = или 2+ 4 – = 0, откуда
= – 2 +

( второй корень квадратного уравнения не удовлетворяет условию, так как должно быть положительным).
Таким образом, для любого > 0 найдено такое > 0, что из неравенства 0 < | x – 2 | < следует неравенство
| x2 – 4 | < ,
т.е. по определению

1.в) Пусть - произвольное положительное число. Требуется доказать, что существует такое число > 0, что при всех значениях х, удовлетворяющих неравенству 0 < | x + 1 | < , будет выполняться неравенство
 или
или
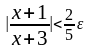 .
.
Не теряя общности можно считать, что < 1.
Поэтому при | x + 1 | < 1 имеем
| x + 3 | = | x
+ 1 + 2 | > 2 – | x + 1| > 2
– 1 = 1. Тогда
 .
.
Чтобы выполнялось неравенство
достаточно, чтобы
 .
.
Таким образом, в качестве
можно взять меньшее из чисел 1 и
 .
.
Итак, для любого > 0 найдено такое > 0, что из неравенства
0 < | x + 1 | <
следует неравенство
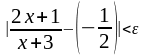 .
.
Таким образом, доказано, что .
Ответ. 1 а)
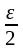 ; 1 б) = – 2
+
или = min
1,
; 1 б) = – 2
+
или = min
1,
 ;
1в) = min
1,
.
;
1в) = min
1,
.
2. а) Так как

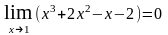 ,
то имеем неопределённость вида
,
то имеем неопределённость вида
 .
Чтобы раскрыть эту неопределённость,
разложим числитель и знаменатель дроби
на множители:
.
Чтобы раскрыть эту неопределённость,
разложим числитель и знаменатель дроби
на множители:
х 3 + 2 х2 – х – 2
=
 (х
– 1) (х2 + 3 х + 2),
(х
– 1) (х2 + 3 х + 2),
х 2– 3 х + 2 = (х – 1) (х – 2).

2. б) Имеем неопределённость вида
.
Чтобы раскрыть эту неопределённость,
умножим числитель и знаменатель дроби
на выражение
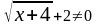 (сопряжённое числителю).
(сопряжённое числителю).
= =
= =
=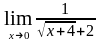 =
=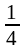 .
.
2в) Имеем неопределённость вида
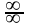 .
Делим числитель и знаменатель почленно
на х 2. Тогда
=
.
Делим числитель и знаменатель почленно
на х 2. Тогда
=
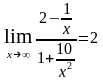 ,
так как
,
так как
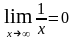 и
и
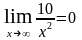 .
.
2. г) Имеем неопределённость вида
– . Умножим и разделим
выражение, стоящее под знаком предела
на
 :
=
:
=
 =
=
 =
=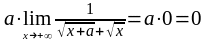 .
.
2. д) Имеем неопределённость вида – . Приведем дроби, стоящие под знаком предела, к общему знаменателю, получим новую дробь, числитель и знаменатель которой стремятся к нулю при х – 2.
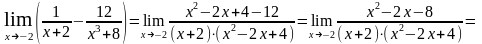
=
2. е) Имеем неопределённость вида 0· . Запишем функцию, стоящую под знаком предела, в другом виде и перейдём к пределу:
= =
= =
= =
=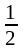 ·1·1=
·1·1=
2. ж) Воспользуемся формулой двойного
угла для функции
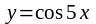 ,
получим
,
получим
 .
.
В
последнем действии умножили числитель
и знаменатель на
 .
.
Воспользовавшись первым замечательным пределом и следствием из него, имеем
 и
и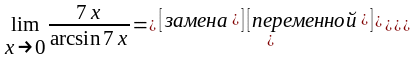 ,
,
продолжим решение исходной задачи:
 .
.
з)
Воспользовавшись вторым замечательным
пределом
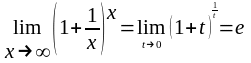 ,
,
получим
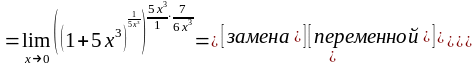

Ответ. 2. а)
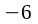 ;
2. б)
;
2. в) 2; 2. г) 0; 2. д)
;
2. б)
;
2. в) 2; 2. г) 0; 2. д)
 ;
2.е)
;
2. ж)
;
2.е)
;
2. ж)
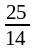 ;
2. з)
;
2. з)
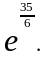
3. а) Так как
 при
при
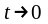 .
Это означает, что
.
Это означает, что и
одну функцию в пределе можно заменить
другой, эквивалентной.
и
одну функцию в пределе можно заменить
другой, эквивалентной.
Поскольку
 при
при
 и
и
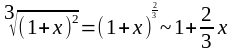 при
,
то
при
,
то
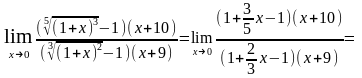
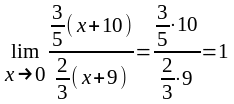 .
.
3.
б) Так как
при
,
 при
,
при
,
 при
,
то
при
,
то
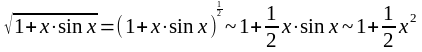 при
.
при
.
 .
.
. Ответ. 3. а) 1; 3. б) .
