Министерство образования РФ

Уфимский государственный авиационный технический университет

Кафедра технической кибернетики

Лабораторная работа №2

Получение на ЭВМ равномерно распределенных

псевдослучайных чисел

Выполнили:

студенты гр. УТС-411

Ганиев И. С.

Беляев В. В.

Садыков Р. Р.

Проверила:

Хасанова Н. В.

Уфа 2007

Цель работы.

Изучение методов получения на ЭВМ равномерно распределенных псевдослучайных чисел и тестов проверки их качества.

Критерий Пирсона.

Методы ( в дальнейшем, тесты ) проверки качества псевдослучайных чисел делятся на три группы:

а) тесты проверки случайности последовательности псевдослучайных чисел;

б) тесты проверки равномерности закона распределения;

в) тесты проверки независимости последовательности.

Первые два теста основываются на статистических критериях согласия, из которых наиболее употребительным является статистический критерий согласия ( Пирсона ).

Пусть имеется  - случайная величина, о законе распределения которой выдвигается некоторая гипотеза, Х - множество возможных значений . Разобьем Х на m попарно непересекающихся множеств Х₁, Х₂,  ,Х_m, таких, что

P  Х_j  = p_j  0 при j = 1, 2, , m,

p₁ + p₂ +  p_m = P  Х  = 1.

Выберем N независимых значений ₁, ₂,  ,_N и обозначим через коли-чество значений Х_j. Очевидно, что математическое ожидание равно Np_j, т.е. М [ ] = Np_j.

В качестве меры отклонения всех от Np_j выбирается величина ( 1 )

При достаточно большом N величина хорошо подчиняется закону распределения с ( m - 1) степенью свободы:

P  , ( 2 )

где - плотность распределения с ( m - 1) степенью свободы.

С помощью формулы ( 2 ) при заданном уровне значимости  ( обычно  = 0.95 ) можно определить нижнюю и верхнюю границы области возможного принятия гипотезы ( доверительного интервала ). Для этого нужно решить соответственно следующие уравнения:

P   = = , ( 3 )

P   = = , ( 4 )

где  = 1  , r = m - 1.

Значения интегралов берутся из таблицы.

P { х } = p,

где х = или х = , p =  или p = .

Эмпирическое математическое ожидание вычисляется по формуле

,

эмпирическая дисперсия

их теоретические значения соответственно 0.5 и 1 / 12.

Для математического ожидания можно для заданного уровня значимости  определить также доверительный интервал:

где  определяется из уравнения:

2Ф = .

Интеграл вероятностей Ф ( х ) = возьмём из таблицы.

Функция распределения и гистограмма частот.

Полезно бывает сравнить также теоретическую функцию распределения и теоретическую плотность распределения случайной величины  с экспери-ментально полученными функцией распределения и гистограммой частот.

Известно, что для случайной величины, равномерно распределенной на интер-вале ( 0, 1 ):

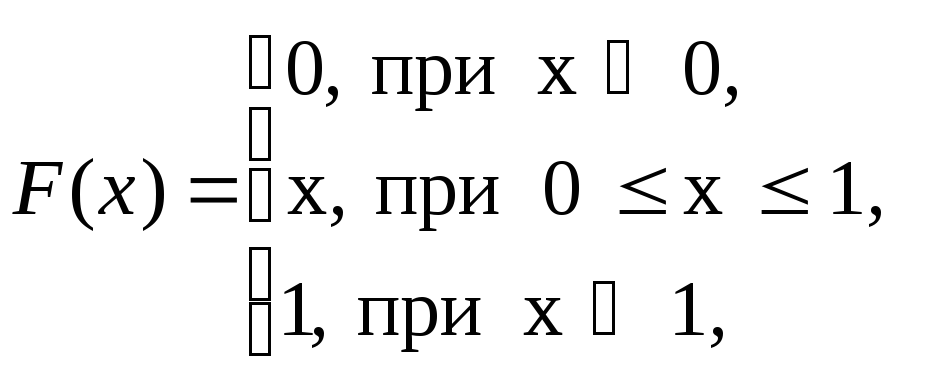
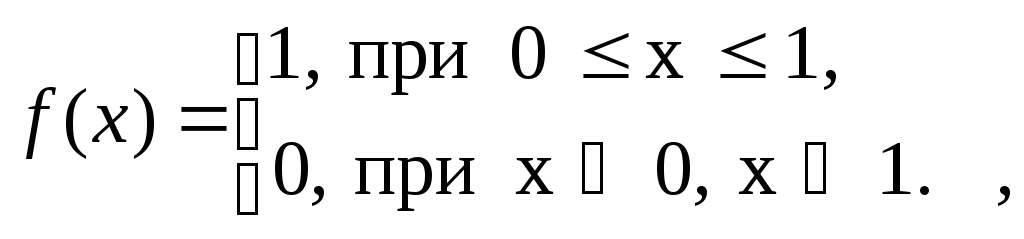
По известной выборке из N значений случайной величины  эксперимен-тальная функция распределения определяется следующим образом:

где равно количеству значений   х.

Гистограмма частот, являющаяся аналогом плотности распределения, строится следующим образом. Весь интервал ( х_min, х_max ) от наименьшего значения х_min до наибольшего значения х_max полученной выборки случайной величины разбивается на q равных промежутков длины h. Затем определяется число значений _i выборки, попавших в i-ый промежуток, после чего для каждого 1  i  q строится прямоугольник с основанием на i-ом промежутке и высотой _i / h. Полученный чертеж называется гистограммой частот или просто гистограммой. Отметим, что при таком построении площадь i-го прямоугольника равна h  ( _i / h ) = _i, т.е. числу значений случайной величины, попавших в i-ый промежуток, а площадь всей гистограммы равна объему выборки.

Листинг программы.

uses crt, graph;

const N=100;

var i,j,gd,gm: integer;

x,hi2,d,c: real;

p: array[1..5] of real;

l: array[1..5] of integer;

q: array[1..N] of real;

g: string[8];

begin

randomize;

clrscr;

p[1]:=0.1;

p[2]:=0.25;

p[3]:=0.2;

p[4]:=0.4;

p[5]:=0.05;

hi2:=0;

c:=0;

for i:=1 to 5 do

l[i]:=0;

for i:=1 to N do begin

x:=random;

q[i]:=x;

c:=c+x;

j:=0;

d:=0;

repeat

j:=j+1;

d:=d+p[j];

until d>=x;

l[j]:=l[j]+1;

end;

for i:=1 to 5 do

hi2:=hi2+sqr(l[i]-N*p[i])/(N*p[i]);

initgraph(gd,gm,'d:\prog\f1.7\bgi');

setcolor(9);

moveto(10,10);

outtext('pj ');

for i:=1 to 5 do begin

str(p[i]:6:2,g);

outtext(g);

end;

moveto(10,25);

outtext('vj ');

for i:=1 to 5 do begin

str(l[i]:6,g);

outtext(g);

end;

outtextxy(10,60,'X^2 prinadlezit doveritelnomu intervalu (0,71<=X^2<=9,5)?');

outtextxy(10,70,'X^2 = ');

str(hi2:5:3,g);

outtextxy(60,70,g);

c:=c/N;

str(c:5:3,g);

outtextxy(10,400,'Empiricheskoe mat. ozidanie:');

outtextxy(10,410,'e~=');

outtextxy(40,410,g);

outtextxy(90,410,'(doverit. interval 0,444<=e~<=0,556)');

for i:=1 to N do

x:=x+sqr(q[i]-c);

x:=x/(N-1);

str(x:5:3,g);

outtextxy(10,420,'Empiricheskaya dispersiya:');

outtextxy(10,430,'s^2=');

outtextxy(50,430,g);

setcolor(14);

line(10,21,350,21);

line(40,10,40,35);

if (hi2>=0.71) and (hi2<=9.5) then

outtextxy(10,80,'da') else

outtextxy(10,80,'net');

line(50,110,50,340);

line(50,330,370,330);

line(46,115,50,110); line(50,110,54,115);

line(365,326,370,330); line(365,334,370,330);

outtextxy(100,100,'Funcii raspredeleniya');

setcolor(10);

d:=0;

for i:=1 to 5 do begin

line(round(300*d)+50,330-round(200*d),round(300*d)+50,330-round(200*(d+p[i])));

d:=d+p[i];

line(round(300*d)+50,330-round(200*d),round(300*(d-p[i]))+50,330-round(200*d));

setcolor(14);

line(round(300*d)+50,327,round(300*d)+50,333);

line(47,330-round(200*d),53,330-round(200*d));

str(d:3:2,g);

if i<>5 then outtextxy(round(300*d)+35,340,g);

outtextxy(10,327-round(200*d),g);

setcolor(6);

setlinestyle(1,0,2);

line(55,330-round(200*d),round(300*(d-p[i]))+50,330-round(200*d));

setlinestyle(0,0,1);

setcolor(10);

end;

line(10,330,50,330);

line(235,218,250,218);

setcolor(12);

line(235,228,250,228);

setcolor(14);

outtextxy(15,105,'F(x)');

outtextxy(373,337,'xj');

outtextxy(347,315,'1');

outtextxy(255,215,'teoretich. F(x)');

outtextxy(255,225,'experiment. F(x)');

setcolor(13);

line(420,130,420,330);

line(420,330,630,330);

line(417,135,420,130); line(423,135,420,130);

line(625,327,630,330); line(625,333,630,330);

outtextxy(390,328-N,'100');

outtextxy(375,120,'vj/pj');

outtextxy(610,335,'pj');

setcolor(9);

outtextxy(450,110,'Gistogramma chastot');

d:=0;

for i:=1 to 5 do begin

d:=d+p[i];

line(round(200*(d-p[i]))+420,330-round(l[i]/p[i]),

round(200*d)+420,330-round(l[i]/p[i]));

line(round(200*d)+420,330-round(l[i]/p[i]),

round(200*d)+420,330);

line(round(200*(d-p[i]))+420,330-round(l[i]/p[i]),

round(200*d)+420,330);

line(round(200*(d-p[i]))+420,330-round(l[i]/p[i]),

round(200*(d-p[i]))+420,330);

end;

setlinestyle(1,0,2);

setcolor(6);

line(419,330-N,630,330-N);

setlinestyle(0,0,1);

readln;

x:=0;

d:=0;

setcolor(12);

for i:=1 to 5 do begin

line(round(300*d)+50,330-round(200*x),round(300*d)+50,330-round(200*(x+l[i]/N)));

x:=x+l[i]/N;

d:=d+p[i];

line(round(300*d)+50,330-round(200*x),round(300*(d-p[i]))+50,330-round(200*x));

end;

readln;

closegraph;

end.

Результаты работы программы.

N=100

β=0,95

pj	0,1	0,25	0,2	0,4	0,05
vj	6	28	20	40	6

χ² = 2,16

χ² принадлежит доверительному интервалу 0,71<= χ² <=9,5

Эмпирическое мат. ожидание:

e` = 0,538 (доверительный интервал 0,444<=e`<=0,556)

незначительно отличается от теоретического (M[x]=0,5).

Эмпирическая дисперсия:

s² = 0,095, что близко к теоретическому значению s² = 0,083.

Критерий согласия Пирсона показал, что распределение случайной величины можно считать (с уровнем значимости β=0,95) равномерным.

Вывод.

Изучили методы получения на ЭВМ равномерно распределенных псевдослучайных чисел. Провели тесты проверки их качества.