Решаем уравнение

F_x() = ₂

Моделируем 

По методу Неймана

Отметим, что функции распределения вида (1) встречаются тогда, когда мы имеем дело со смесью случайных величин, т.е.  порождается некоторой совокупностью случайных величин. Однако представление (1) часто придумывают искусственно, чтобы облегчить (ускорить) процедуру моделирования . При этом, сложным выражениям F_X(х) (т.е. требующим для своего моделирования много времени) присваиваются малые веса С_X , что ведет к значительному ускорению процесса моделирования случайной величины  (т.к. сложные распределения 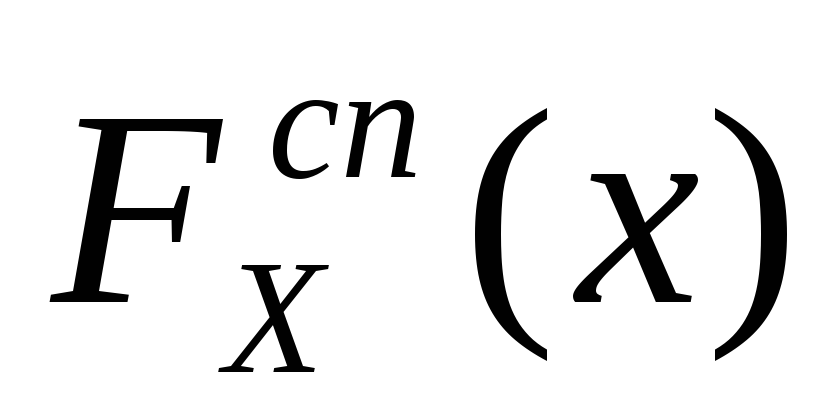будут моделироваться гораздо реже, чем простые ).

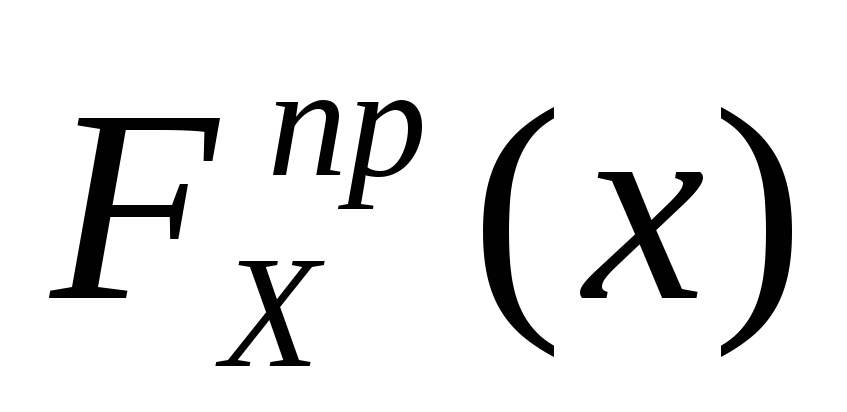Для моделирования выберем метод обратных функций.

Листинг программы:

uses crt;

var i,c: integer;

x,q,w: real;

begin

randomize;

clrscr;

writeln('q - ravnomerno raspredel. sl. velichina');

writeln('x - sl. vel. s odnoi iz plotnostei veroyatnosti');

writeln(' 1. f(x)=tg(x)/ln(sqrt(2)), ves - 0,3');

writeln(' 2. f(x)=4/Pi , ves - 0,7');

writeln(' x=0..Pi/4');

writeln;

writeln('q ');

writeln('n ');

writeln('# ');

for i:=1 to 10 do begin

q:=random;

w:=random;

c:=2;

if w<0.3 then begin

x:=arctan(sqrt(exp(q*ln(2))-1));

c:=1;

end;

if w>=0.3 then

x:=q*Pi/4;

gotoxy((i-1)*6+4,7);

write(q:6:2);

gotoxy((i-1)*6+4,8);

write(x:6:2);

gotoxy((i-1)*6+4,9);

write(c:6);

end;

readln;

end.

Результат выполнения программы:

q - ravnomerno raspredel. sl. velichina

x - sl. vel. s odnoi iz plotnostei veroyatnosti

1. f(x)=tg(x)/ln(sqrt(2)), ves - 0,3

2. f(x)=4/Pi , ves - 0,7

x=0..Pi/4

q 0.74 0.86 0.85 0.27 0.56 0.10 0.84 0.79 0.79 0.59

n 0.58 0.68 0.73 0.43 0.44 0.26 0.66 0.62 0.62 0.62

# 2 2 1 1 2 1 2 2 2 1

Выводы.

Изучили методы моделирования дискретных и непрерывных случайных величин с заданным законом распределения.