Министерство образования РФ

Уфимский государственный авиационный технический университет

Кафедра технической кибернетики

Лабораторная работа №1

Моделирование на ЦВМ случайных величин с заданным законом распределения.

Выполнили:

студенты гр. УТС-411

Беляев В. В.

Ганиев И. С.

Проверила:

Хасанова

Уфа 2007

Цель работы.

Изучение методов моделирования на ЦВМ дискретных и непрерывных случайных величин, имеющих заданный закон распределения.

1. Моделирование дискретных случайных величин.

Пусть дискретная случайная величина x задала своим распределением

xi	1	2	3	4	5
Pi	0,1	0,25	0,2	0,4	0,05

Интервал (0,1) изменения равномерно распределенной случайной величины  разделим на интервалы _i , такие, что длина _i равна P_i .

₁ ₂ ₃ _n У

0

Тогда случайная величина x получается по следующей формуле:

x=x_i , если  _i

Блок-схема алгоритма моделирования дискретной случайной величины x имеет следующий вид:

m:=1

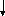
Получаем 

₁:=X_m

m:=1

да

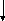
нет

m:=m+1

Листинг программы:

uses crt;

var e,q: real;

i,c: integer;

h,k: array[1..7] of real;

const

x: array[1..5] of integer=(1, 2, 3, 4, 5);

p: array[1..5] of real=(0.1, 0.25, 0.2, 0.4, 0.05);

begin

clrscr;

randomize;

writeln('Число экспериментов: 7');

for i:=1 to 5 do h[i]:=0.0;

for i:=1 to 7 do begin

e:=random;

c:=0; q:=0;

repeat

c:=c+1;

q:=q+p[c];

until q>=e;

h[i]:=e;

k[i]:=x[c];

end;

write('Дискр. сл. число: ');

for i:=1 to 5 do

write(x[i]:4,' ');

writeln;

write('Исх. вер-ти: ');

for i:=1 to 5 do

write(p[i]:3:2,' ');

writeln;

writeln;

write('Непр. сл. число (e): ');

for i:=1 to 7 do

write(h[i]:3:2,' ');

writeln;

write(' Дискр. сл. число (x): ');

for i:=1 to 7 do

write(k[i]:3:2,' ');

readln;

end.

Результат выполнения программы:

Число экспериментов: 7

Дискр. сл. число: 1 2 3 4 5

Исх. вер-ти: 0.10 0.25 0.20 0.40 0.05

Непр. сл. число (e): 0.08 0.50 0.82 0.15 0.33 0.44 0.95

Дискр. сл. число (х): 1.00 3.00 4.00 2.00 2.00 3.00 4.00

2. Моделирование непрерывных случайных величин.

Метод обратных функций.

Данный метод является непрерывным аналогом метода моделирования дискретных случайных величин, описанного в разделе 1. Пусть необходимо смоделировать случайную величину x(a,b) , заданную плотностью распределения р(х).

Обозначим через F(х)= функцию распределения случайной величины x.

Тогда случайная величина x , полученная путем решения уравнения

F(x)=,

где  - равномерно распределенная на интервале (0,1) случайная величина, имеет плотность распределения p (х).

Блок-схема алгоритма моделирования случайной величины x по методу обратных функций: