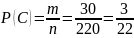Аксиоматическое определение вероятности
Пусть множество всех возможных исходов некоторого опыта (эксперимента). Согласно аксиоматическому определению вероятности, каждому событию А (А – подмножество множества Ω) ставится в соответствии некоторое число Р(А), называемое вероятностью события А, причем так, что выполняются следующие три условия (аксиомы вероятностей):
1.
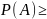0
2.
3.
аксиома сложения:
,
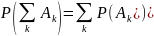если Аi · Аj = Ø, т. е. вероятность суммы попарно-несовместных событий равна сумме вероятностей этих событий.
Из аксиом (1)—(3) вытекают основные свойства вероятности:
1. Р(Ø) = 0, т. е. вероятность невозможного события равна нулю.
2.
.
3. для любого события А.
4.
,
если
.
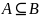5.
,
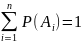если
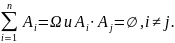
Если
множество Ω состоит из п равновозможных
элементарных событий
(т. е.
),
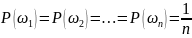то вероятность события А определяется
по формуле классического определения
вероятности
,
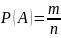где m число случаев (элементов) , принадлежащих множеству А (число благоприятствующих событию А исходов), п число элементов множества Ω (число всех исходов опыта).
3.1. В урне содержится 5 белых и 4 черных шара различающихся только цветом.
1) Вынимается наудачу один шар. Найти вероятность того, что он белый.
2) Вынимаются наудачу два шара. Найти вероятность того, что: а) оба шара белые; б) хотя бы один из них черный.
О 1) Перенумеруем шары. Пространство элементарных событий можно записать в виде = {Б1, Б2, Б3, Б4, Б5, Ч1, Ч2, Ч3, Ч4}. Пусть событие А = {появление белого шара}, тогда А = {Б1, Б2, Б3, Б4, Б5}.
Так
как все элементарные исходы равновозможны,
то по классическому определению
вероятности
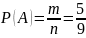
2) При вынимании двух шаров возможны такие исходы: (Б1,Ч1), (Б2, Б3), (Б3, Б2), (Ч4, Б5) и т.д. Число всех случаев равно
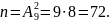
а)
Исходами благоприятствующими наступлению
события В = {появление двух белых
шаров} являются (Б1, Б2), (Б1, Б3), (Б3, Б5), (Б3,
Б1) и т.д. Число таких случаев равно
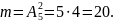
Поэтому
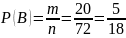
б)
Исходами благоприятствующими наступлению
события С = {появление хотя бы одного
черного шара} являются (Б1, Ч1), (Б1, Ч2),
(Б1, Ч3), (Ч3, Б1), (Ч1, Ч2), (Ч3, Ч4) и т. д. Число
таких случаев равно
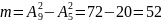(в 20 случаях из 72 появятся два белых шара
(см. пункт а), поэтому в остальных
случаях хотя бы один из пары шаров будет
черным. Отсюда
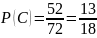. Этот же результат можно получить иначе,
т.к. С =
,
то Р(С) = Р(
)
= 1—Р(В) =
.
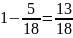3.2. В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Какова вероятность того, что:
а) все они одного цвета;
б) все они разных цветов;
в) среди них 2 синих и 1 зеленый карандаш.
О
Сначала заметим, что число способов
выбрать 3 карандаша из 12 имеющихся в
наличии равно
.
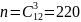а)
Выбрать 3 синих карандаша из 5 можно
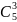способами;
3 красных из имеющихся 4 можно выбрать
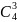способами; 3 зеленых из 3 зеленых —
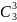способами.
По
правилу сложения общее число т случаев,
благоприятствующих событию А = {три
карандаша, вынутых из коробки, одного
цвета}, равно
.
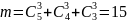Отсюда
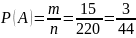
б)
Пусть событие В = {три вынутых
карандаша разных цветов}. Число т
исходов, благоприятствующих наступлению
события В, по правилу умножения
равно
Поэтому
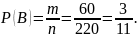
в)
Пусть событие С = {из трех выбранных
карандашей 2 синих и 1 зеленый}. Выбрать
2 синих карандаша из имеющихся 5 синих
можно
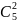способами,
а 1 зеленый из имеющихся 3 зеленых –
способами.
Отсюда по правилу умножения имеем:
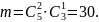Поэтому
