Дополнительные задания
2.28. Построить пространство Ω для следующих испытаний:
а) Монета бросается до первого появления герба или до тех пор, пока решка выпадет три раза подряд;
б) подбрасывается игральная кость, а затем монета.
2.29. В урне находится 10 одинаковых шаров занумерованных числами 0,1,2.. 9. Из нее извлекаются по одному 4 шара. После каждого извлечения вынутый шар возвращается обратно. Описать пространство Ω для этого эксперимента и найти число его элементов.
2.30. Из четырех карточек с номерами 1, 2, 3, 4 последовательно наудачу выбирают две. Составить пространство элементарных событий для этого опыта, если его элементами служат:
а) двузначные числа образованные извлеченными карточками;
б) суммы номеров, извлеченных карточек.
2.31. Назвать противоположные события для следующих событий:
а) А (выигрыш 1-го игрока в шахматной партии);
б) В = {произошло хотя бы одно попадание при десяти выстрелах};
в) С = {произошло три попадания при трех выстрелах};
г) D = {произошло не более двух попаданий при пяти выстрелах};
д) E = {в семейной паре муж старше жены}.
2.37. Электрическая цепь с выключателями составлена по схеме, приведенной на рисунке 3. Пусть событие Аi = {включен выключатель с номером i}, i = 1,2,..., 5.
а) для схемы рис. 62 а записать через Аi событие А = {ток идет};
б) для схемы рис. 62 б записать через А события А и .
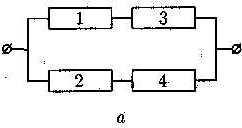Рис.3
а
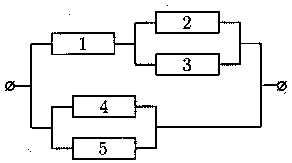Рис.3
б
§ 3. Вероятность случайного события
Классическое определение вероятности
Вероятность события численно характеризует степень возможности его появления в рассматриваемом опыте.
Пусть производится опыт с п равновозможными исходами, образующими полную группу несовместных событий. Такие исходы называются элементарными исходами (событиями), случаями, шансами. Случай, который приводит к наступлению события А называется благоприятным (или благоприятствующим) ему.
Вероятностью события А называется отношение числа M случаев благоприятствующих этому событию, к общему числу N случаев.
Такое определение вероятности называется классическим.
Из классического определения следуют свойства вероятности:
1.
2.
3.
4.
5. P(A) = P(A) + P(B)
Геометрическое определение вероятности
Обобщение понятия «классической вероятности» на случай опытов с бесконечным (вообще говоря, несчетным) числом исходов является понятие «геометрической вероятности». К этому понятию приводят задачи на подсчет вероятности попадания точки в некую область (отрезок, часть плоскости, часть тела и т.д.).
Пусть пространство элементарных событий Ω‚ представляет собой некоторую область плоскости. Тогда в качестве событий могут рассматриваться области А содержащиеся в Ω.
Вероятность попадания в область А точки, наудачу выбранной из области Ω, называется геометрической вероятностью события А и находится по формуле
,
где S(А) и S(Ω) площади областей А и Ω соответственно.
Случай, когда представляет собой отрезок или трехмерную область, рассматривается аналогично.