2. Определение количества интервалов и моментов переключения управляющего воздействия

В соответствии с (3.8) управляющее воздействие скачком принимает значениe +u_max или –u_max. Это уравнение дает только качественную сторону изменения управляющего воздействия. Вместе с тем, при проектировании системы нужно знать и количественные характеристики такие, как количество интервалов максимального значения управляющего воздействия и моменты переключения этого воздействия. Количество интервалов легко определить, пользуясь теоремой об n - интервалах, основное содержание которой заключается в следующем.

Если С – часть системы описывается линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами и корни его характеристического уравнения отрицательные вещественные или нулевые, то количество интервалов максимального значения управляющего воздействия должно быть n, а знаки на интервалах должны чередоваться (n-1) раз.

Таким образом, число интервалов определяем по корням характеристического уравнения С – части системы. Рассмотрим определение моментов переключения в разомкнутой системе, основываясь на работах. Моменты переключения зависят от многих факторов:

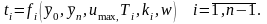(3.9)

Определение зависимости (3.9) довольно сложная задача, трудности в решении которой значительно возрастают при учете возмущающих воздействий w. Ограничимся определением моментов переключения как функции начального 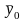и конечного 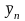значения вектора состояния системы. Для нахождения этой функции применим метод стыкования решений дифференциальных уравнений со знакопеременной правой частью на примере звена второго порядка.

Пример 3.1. С – часть системы описывается уравнением

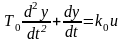, (3.10)

10

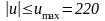где Т₀=0,61 с; k₀=2,310^-3; ед.

Управляющее воздействие может изменять знак не более одного раза. С учетом знака 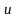перепишем (4.6)

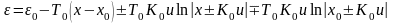. (4.7)

Обозначим 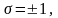тогда

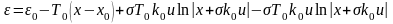. (4.8)

Принимая из начальных условий , получим

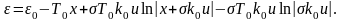(4.9)

Уравнению (4.9) соответствуют фазовые траектории 1, изображенные на рис. 4.1 Определим уравнение фазовой траектории, проходящей через начало координат, где , .

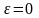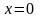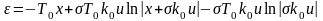. (4.10)

Уравнение (4.10) является уравнением линии переключения (траектория NOM - кривая 2). Эта траектория является единственной, по которой можно попасть в начало координат.

На линии переключения имеет место равенство 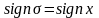, с учетом которого получим функцию переключения

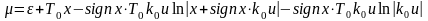. (4.11)

Уравнение (4.11) используется для построения замкнутой, оптимальной по быстродействию системы, С-часть которой описывается уравнением (3.10).

23

Найдем уравнения для построения линии переключения и фазовой траектории системы, в которой уравнение С-части имеет вид (3.23)

.

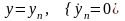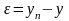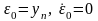Требуется перевести координаты объекта из начального состояния в конечное за минимальное время. Будем оперировать ошибкой системы . При этом в начале управления ошибка максимальна, по мере приближения к заданному состоянию ошибка уменьшается и становится равной нулю в заданной точке. Таким образом, задача заключается в переводе в фазовой плоскости вектора ошибки из состояния при t = 0 в состояние 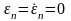за минимальное время.