3.10. Геометрический смысл аффинных координат

Рассмотрим прямую O и вектор , коллинеарный вектору . Тогда, как следует из теоремы 3.1.2, , причем

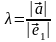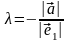, если ,

, если .

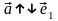Определение 3.10.1. Указанное число  называется алгебраической мерой вектора 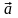на оси, определяемой вектором , и обозначается .

С учетом введенного обозначения, очевидно, что .

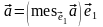Лемма 3.10.1. Для любых трех коллинеарных векторов 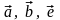и произвольного числа  справедливы соотношения

.

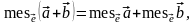
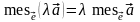Доказательство. Пусть . По определению алгебраической меры вектора

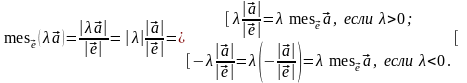
Если 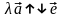, то

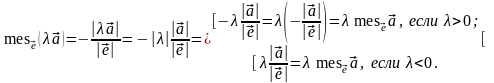
Рассмотрим теперь алгебраическую меру суммы векторов. По условию векторы являются коллинеарными, поэтому пусть . Тогда

.

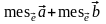Таким образом, можно утверждать, что аффинная координата произвольной точки M на координатной оси равна алгебраической мере ее радиус-вектора .

П

Рис. 3.10.1

усть задана аффинная система координат O и произвольный вектор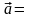 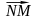. Спроектируем начало и конец данного вектора на координатные оси, получаем соответственно 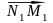и .

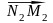Определение 3.10.2. Вектор ( ) называется геометрической проекцией вектора на координатную ось O (O ).

Для геометрической проекции вектора на координатные оси будем использовать обозначение , .

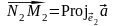В соответствии с правилом параллелограмма

.

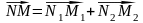
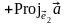С другой стороны, векторы 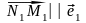, , 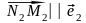поэтому

,

+ .

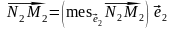
Определение 3.10.3. Алгебраическая мера геометрической проекции вектора на координатную ось называется алгебраической проекцией вектора.

Алгебраическая проекция вектора на ось O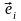 обозначается 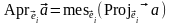. С учетом введенного обозначения вектор

,

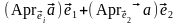т. е. аффинными координатами произвольного вектора являются его алгебраические проекции на координатные оси, а аффинными координатами произвольной точки — алгебраические проекции ее радиус-вектора на соответствующие координатные оси.

Допустим теперь, что в системе координат O задан произвольный вектор . Спроектируем точки N и M на координатные оси. Тогда точки N₁ и M₁ определяют вектор , точки N₂ и M₂ — вектор , а точки N₃ и M₃ — соответственно вектор 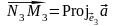. В соответствии с правилом сложения векторов

.

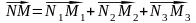
Следовательно, аффинные координаты произвольного вектора есть его алгебраические проекции на координатные оси, а аффинные координаты произвольной точки — алгебраические проекции ее радиус-вектора на соответствующие координатные оси.

Вопросы и упражнения

1. Является ли окружность с радиусом R аффинным пространством?

Ответ: 1) Нет, так как окружности нельзя сопоставить присоединенное пространство; 2) да, при условии, что R конечное число; 3) нет, поскольку не выполнены аксиомы; 4) да, если окружность имеет бесконечный радиус.

2. Какова будет ориентация правой тройки после перестановки рядом стоящих векторов?

Ответ: 1) правая; 2) левая.

3. Дан параллелограмм OABC, причем 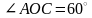, 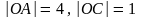. Приняв за базис векторы 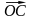и 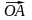, найти аффинные координаты основания высоты параллелограмма, опущенной из точки A.

Ответ: (2, 0).

4. Определить аффинные координаты вершин правильного шестиугольника, сторона которого равна 1, если за координатные оси приняты две смежные его стороны, причем вершина, противолежащая началу координат, имеет положительные координаты.

Ответ: (0, 0), (1, 0), (2, 1), (2, 2), (1, 2), (0, 1).

5. В аффинной системе координат угол между ортами и равен . Определить координаты точки, симметричной точке 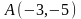относительно координатной оси .

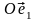Ответ: .

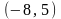8