
- •Введение
- •1. Основные понятия теории вероятностей
- •2. Повторение незавИсИмых опытов
- •3. Случайные величины и их числовые характеристики
- •4. Система двух случайных величин и регрессия
- •Закон распределения двумерной случайной величины
- •5. Основы математической статистики
- •Контрольная работа 4
- •Задача 2.
- •Контрольная работа 5
- •6. Линейное программирование. Основные понятия и экономическая интерпретация
- •6.1. Задача лп
- •6.2. Примеры постановки задач лп
- •6.3. Геометрическая интерпретация задачи лп. Графическое решение
- •6.4. Основные формы задачи лп
- •6.5. Симплексный метод и приведение задачи лп к правильной форме
- •6.6. Признаки оптимальности начального допустимого плана
- •7. Метод искусственного базиса
- •8. Двойственные задачи лп
- •9. Транспортная задача и метод потенциалов
- •Контрольная работа 6
- •Рекомендательный библиографический список
- •Значения в зависимости от числа степеней свободы m и уровня значимости ( – доверительная вероятность)
- •Содержание
6.6. Признаки оптимальности начального допустимого плана
Теорема 1. Пусть
в правильной задаче ЛП целевая функция
![]() ,
где
,
,
…,
,
где
,
,
…,
![]() – базисные, а
– базисные, а
![]() ,
…,
,
…,
![]() – свободные переменные. Тогда:
– свободные переменные. Тогда:
1) если все
![]()
![]() ,
то начальный допустимый план
,
то начальный допустимый план
![]() – единственный оптимальный (т.е.
– единственный оптимальный (т.е.
![]() );
);
2) если все
![]() ,
то оптимальные планы имеют вид: для
свободная переменная
,
то оптимальные планы имеют вид: для
свободная переменная
![]() ;
для
;
для
![]() свободная переменная
свободная переменная
![]() – произвольная, но удовлетворяющая
всем ограничениям; базисные переменные
выражаются через свободные переменные
из ограничений.
– произвольная, но удовлетворяющая
всем ограничениям; базисные переменные
выражаются через свободные переменные
из ограничений.
Следствие.
Если все
и есть коэффициенты
,
то по формуле (2) имеем бесконечное
множество решений (альтернативные
оптимальные планы), для которых оптимальное
значение одинаково
![]() .
.
Теорема 2.
Если в правильной задаче ЛП в целевой
функции есть коэффициент при свободной
переменной
![]() ,
возможны следующие случаи:
,
возможны следующие случаи:
1) при наличии среди коэффициентов ограничений соответствующего столбца хоть одного положительного начальный допустимый план можно улучшить, взяв этот столбец за ключевой и сделав симплексное преобразование;
2) при условии,
что все коэффициенты ограничений этого
столбца
,
задача ЛП не имеет решения
![]() .
.
Следствие. Если в правильной задаче ЛП все коэффициенты целевой функции при свободных переменных неотрицательны, то оптимальность достигнута. В этом случае имеется одно решение при условии, что все коэффициенты , и множество решений при условии, что есть хоть одно . Если же есть отрицательный коэффициент целевой функции при свободной переменной, то оптимальности нет. В этом случае или возможно симплексное преобразование (которое улучшит начальный допустимый план), или проделать симплексное преобразование невозможно, и задача ЛП неразрешима.
Например, для правильной формы
примера 18 для единственной свободной
переменной
![]() коэффициент в целевой функции
коэффициент в целевой функции
![]() и поэтому оптимальное решение
и
и поэтому оптимальное решение
и
![]() .
.
Пример 19. Найдем решение для задачи ЛП:
![]() ,
,
где ограничения
![]()
Расширенная матрица задачи
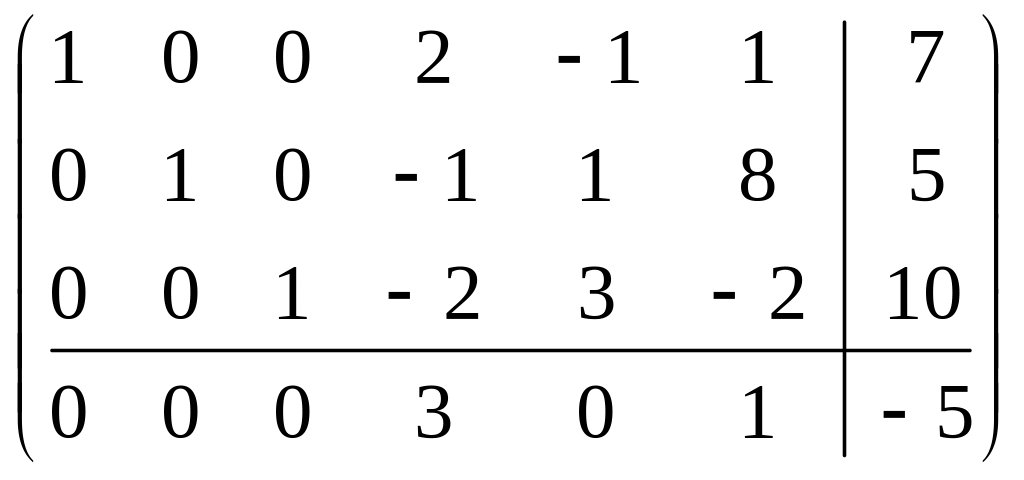
имеет правильную форму. При
свободных переменных
,
и
коэффициенты неотрицательные, а значит,
оптимальность достигнута, но так как
коэффициент
![]() (при
(при
![]() ),
то имеются альтернативные оптимальные
решения. Коэффициенты
),
то имеются альтернативные оптимальные
решения. Коэффициенты
![]() и
и
![]() и поэтому свободные переменные
и поэтому свободные переменные
![]() и
и
![]() .
Свободная переменная
,
у которой
.
Свободная переменная
,
у которой
![]() ,
должна удовлетворять всем ограничениям
,
должна удовлетворять всем ограничениям
![]() :
:
![]()
![]()
![]()
![]() .
.
Выражая базисные переменные , и через свободную , получим общий вид оптимальных решений (общее решение)
![]() ,
,
где .
Оптимальное
значение
![]() .
.
Пример 20. В условиях примера 16 найти оптимальное решение симплексным методом.
Решение. Приведем задачу к каноническому виду
![]() ,
,
![]()
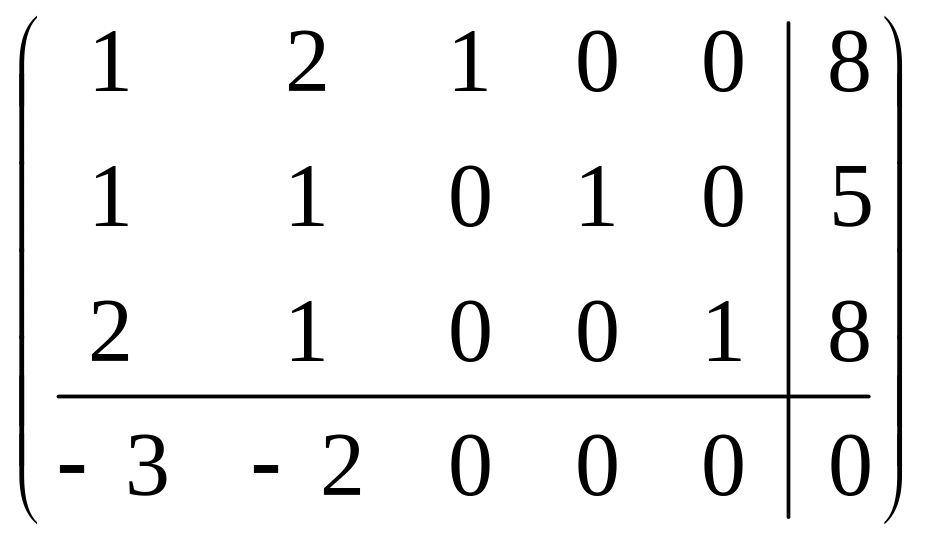 .
.
это правильная форма с отрицательными коэффициентами при свободных переменных в целевой функции.
Проведем симплексные преобразования (теорема 2, п.1).
Находим минимум отношений для первого столбца
![]() .
.
Проводим симплексные преобразования для этого ключевого элемента

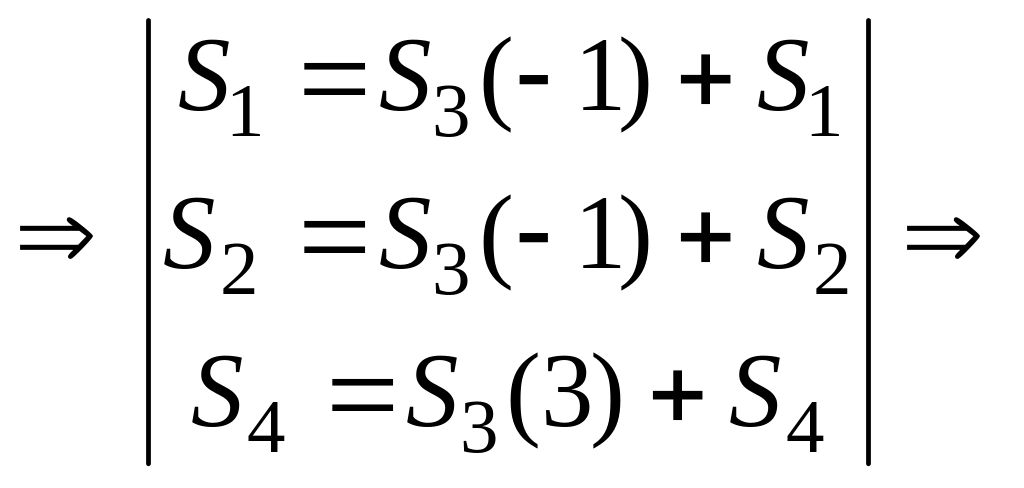
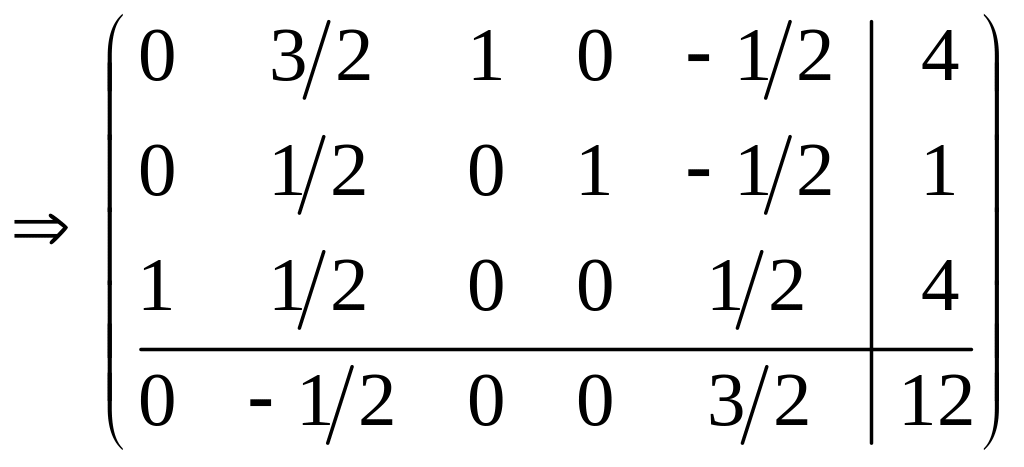 .
.
Снова находим минимум отношений для второго столбца (отрицательный коэффициент целевой функции –1/2)
![]() .
.
Проводим симплексные преобразования для этого ключевого элемента:
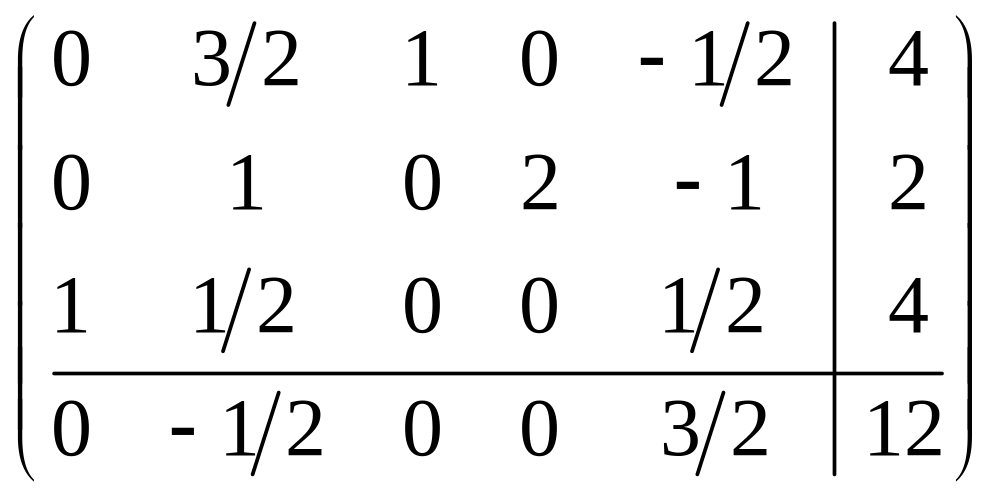
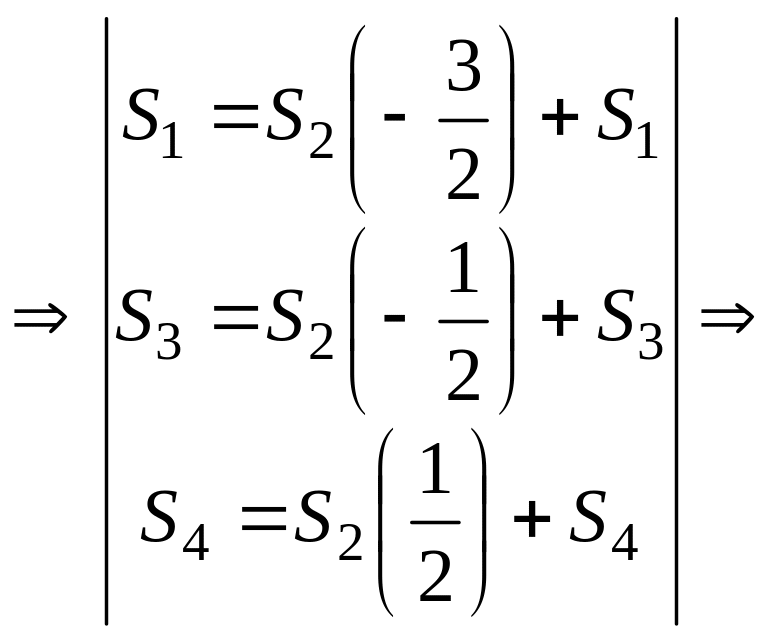
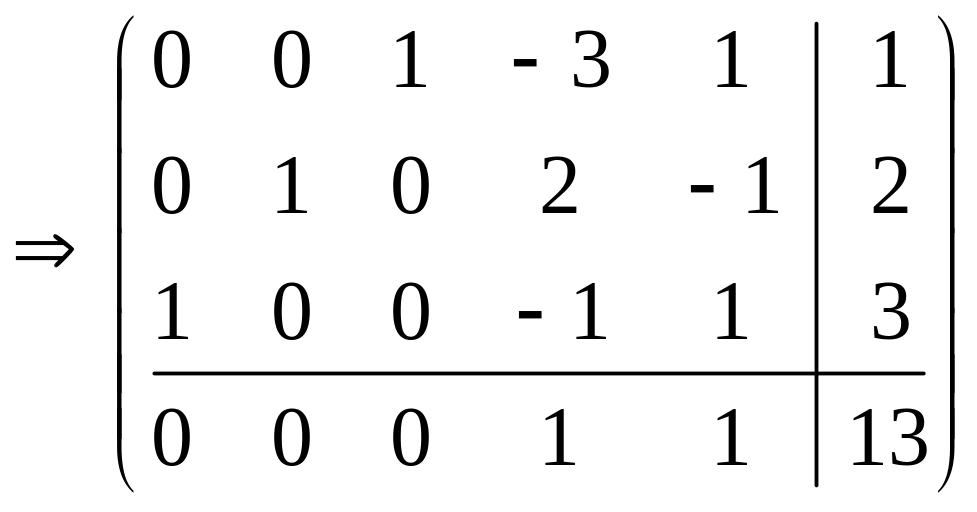 .
.
Так как все
коэффициенты целевой функции при
свободных переменных х4, х5
больше нуля, по теореме 1 имеем
единственное оптимальное решение
![]() ,
для которого
,
для которого
![]() ,
,
![]() и
и
![]() .
.
