
- •Введение
- •1. Основные понятия теории вероятностей
- •2. Повторение незавИсИмых опытов
- •3. Случайные величины и их числовые характеристики
- •4. Система двух случайных величин и регрессия
- •Закон распределения двумерной случайной величины
- •5. Основы математической статистики
- •Контрольная работа 4
- •Задача 2.
- •Контрольная работа 5
- •6. Линейное программирование. Основные понятия и экономическая интерпретация
- •6.1. Задача лп
- •6.2. Примеры постановки задач лп
- •6.3. Геометрическая интерпретация задачи лп. Графическое решение
- •6.4. Основные формы задачи лп
- •6.5. Симплексный метод и приведение задачи лп к правильной форме
- •6.6. Признаки оптимальности начального допустимого плана
- •7. Метод искусственного базиса
- •8. Двойственные задачи лп
- •9. Транспортная задача и метод потенциалов
- •Контрольная работа 6
- •Рекомендательный библиографический список
- •Значения в зависимости от числа степеней свободы m и уровня значимости ( – доверительная вероятность)
- •Содержание
6.5. Симплексный метод и приведение задачи лп к правильной форме
Для приведения канонической задачи ЛП к правильной форме и улучшения начального допустимого плана (перехода к другому начальному допустимому плану, значение целевой функции которого меньше) используется симплексный метод (фактически метод Жордана – Гаусса при особом выборе разрешающего или ключевого элемента).
Пусть в столбце
![]() матрицы A, где
необходимо получить нули и единицу
(ключевой столбец), минимум отношения
ресурсов
матрицы A, где
необходимо получить нули и единицу
(ключевой столбец), минимум отношения
ресурсов ![]() к соответствующим положительным
элементам этого столбца
к соответствующим положительным
элементам этого столбца
![]() достигается в строке
достигается в строке
![]() (ключевая строка): для ключевого элемента
(ключевая строка): для ключевого элемента
![]() выполняется
выполняется
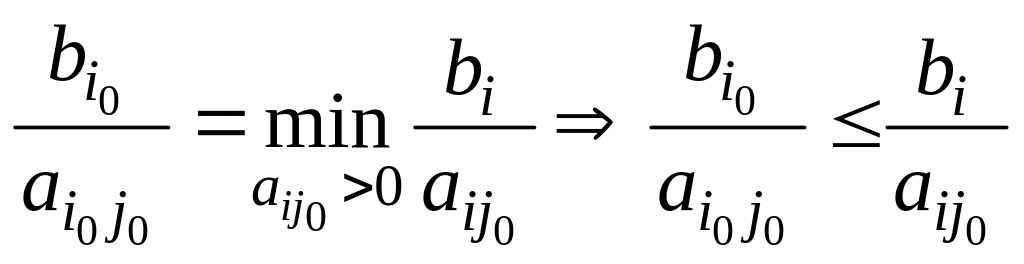 для любого
для любого
![]() .
.
Тогда при исключении
![]() при помощи ключевого элемента
получим новую правую часть
при помощи ключевого элемента
получим новую правую часть
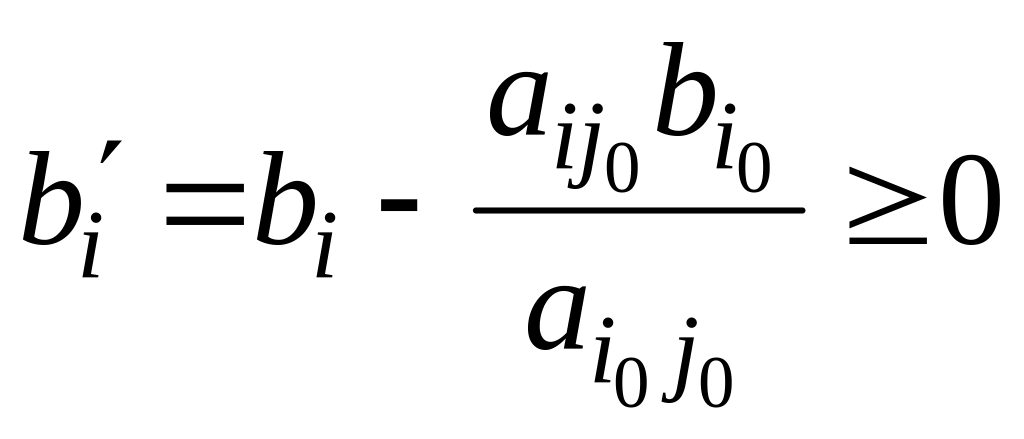 при
при
![]() ,
а при
,
а при
![]() также
также
 .
.
Таким образом,
при таком выборе ключевого элемента не
нарушается каноничность задачи, и после
использования преобразования Жордана
– Гаусса получим правильный столбец.
Такое преобразование называется
симплексным. Обычно при приведении к
правильному виду в качестве ключевого
столбца выбирается тот, у которого в
дополнительной строке стоит наименьший
коэффициент
![]() целевой функции, если над ним в столбце
имеется
.
При этом новая ключевая строка не должна
совпадать с полученной ранее, чтобы не
испортить уже полученные правильные
столбцы. Проводя такие преобразования,
приходим либо к правильной форме
(отбрасывая как в методе Гаусса нулевые
строки-тождества), либо получим (как в
методе Гаусса) невозможное равенство
вида
целевой функции, если над ним в столбце
имеется
.
При этом новая ключевая строка не должна
совпадать с полученной ранее, чтобы не
испортить уже полученные правильные
столбцы. Проводя такие преобразования,
приходим либо к правильной форме
(отбрасывая как в методе Гаусса нулевые
строки-тождества), либо получим (как в
методе Гаусса) невозможное равенство
вида
![]() ,
,
где
![]() ,
,
![]() и
и
![]() .
.
В последнем случае ограничения задачи несовместны (область Ǿ) и задача ЛП неразрешима.
Если симплексное преобразование применяется к правильной задаче для улучшения начального допустимого плана, то, выбрав новый ключевой столбец (новую базисную переменную из числа старых свободных переменных) и проведя симплексное преобразование, изменим какой-нибудь старый правильный столбец. Фактически будет осуществляться переход к новой вершине симплекса и если решение есть, то, перебрав несколько вершин (а их в симплексе конечное число!), найдется вершина, где значение целевой функции будет оптимальным (наименьшим).
Замечание.
Если при наличии некоторых значений
![]() ,
возникает повтор правильных столбцов
(зацикливание), то выход из цикла
осуществляется выбором ключевого
столбца, не совпадающего со столбцами
из цикла.
,
возникает повтор правильных столбцов
(зацикливание), то выход из цикла
осуществляется выбором ключевого
столбца, не совпадающего со столбцами
из цикла.
Пример 18. Приведем к правильной форме каноническую задачу ЛП
![]() ,
,
,
,
где ограничения
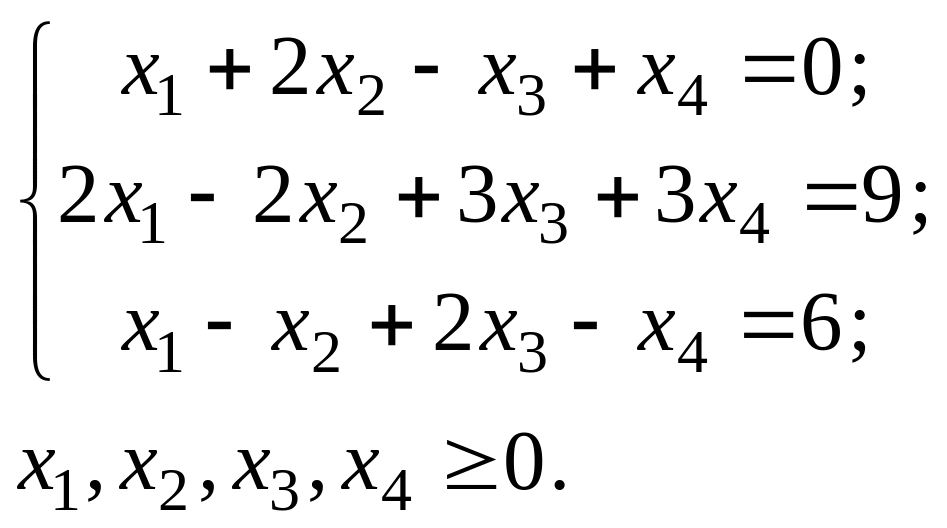
Расширенная матрица этой задачи записывается следующим образом:
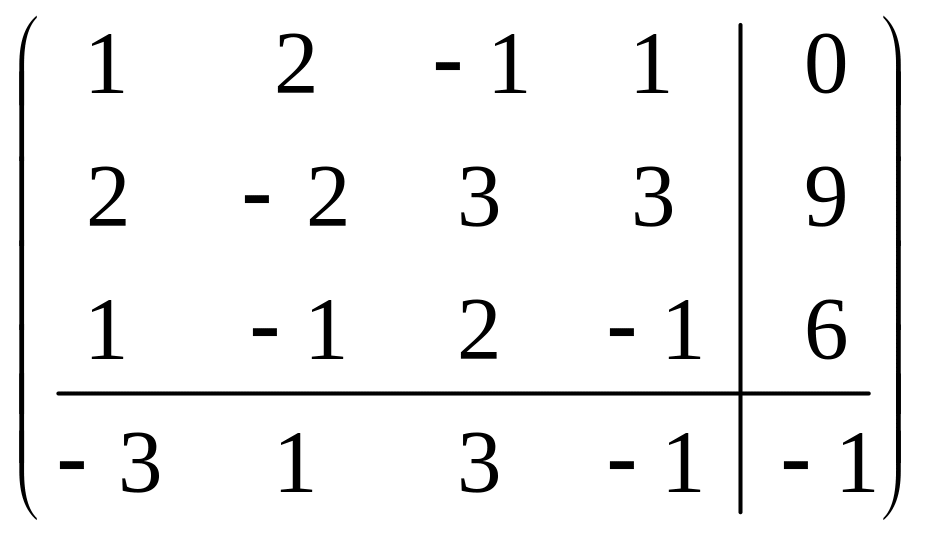 .
.
Выбираем первый столбец за ключевой и ключевой элемент а11 из минимума отношений
![]() .
.
Проделаем симплексное преобразование над первым столбцом (Si – строки):
![]() .
.
Следовательно, новая форма
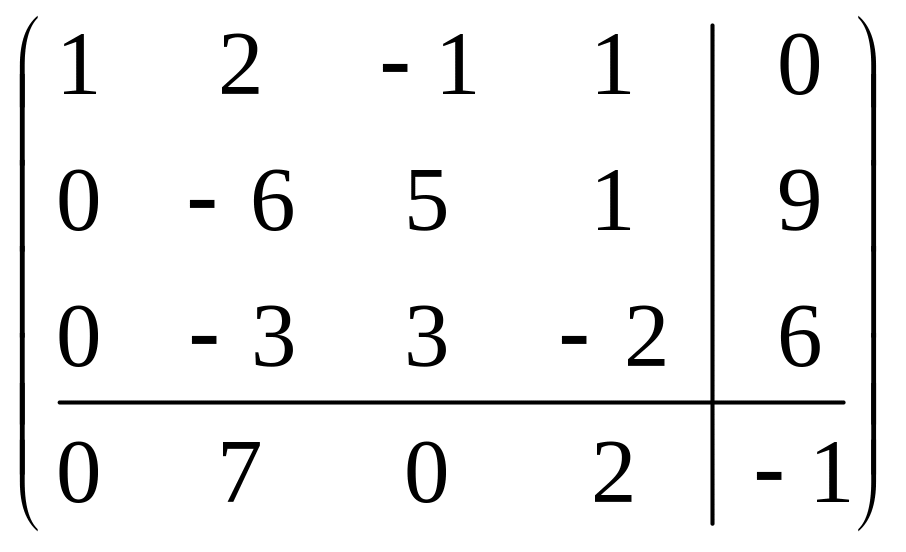 .
.
В матрице снова находим новый ключевой столбец (третий) и ключевой элемент а23:
min![]() .
.
Получая на месте а23 единицу, имеем матрицу
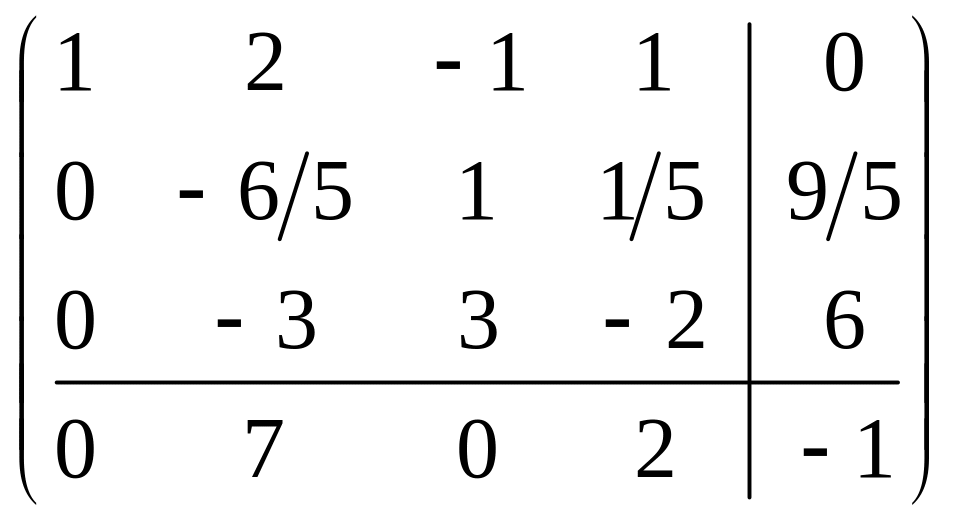
![]()
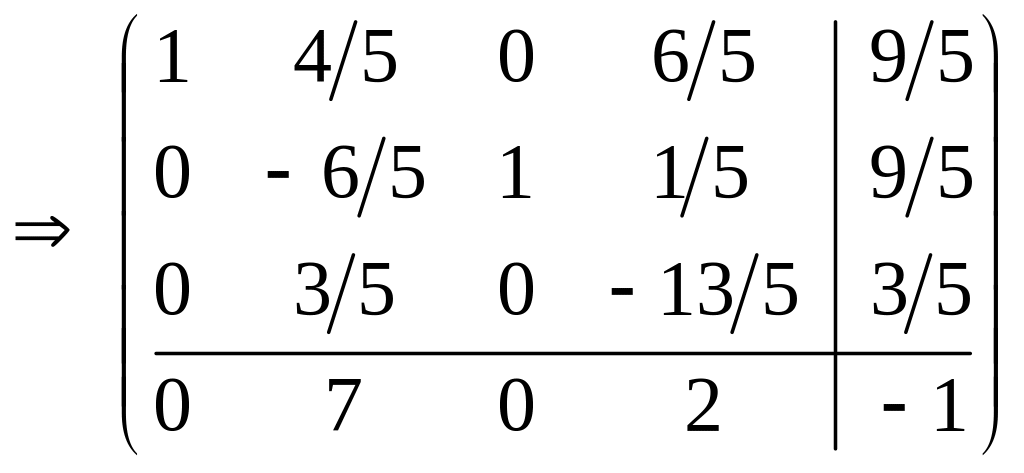 .
.
в
качестве ключевого возьмем второй
столбец, потому что выбор четвертого
столбца, где
![]() ,
и ключевой элемент 6/5, изменит первый
правильный столбец.
,
и ключевой элемент 6/5, изменит первый
правильный столбец.
Так как
![]() ,
то в качестве ключевого элемента примем
а12 = 4/5.
,
то в качестве ключевого элемента примем
а12 = 4/5.
Проделаем симплексные преобразования:
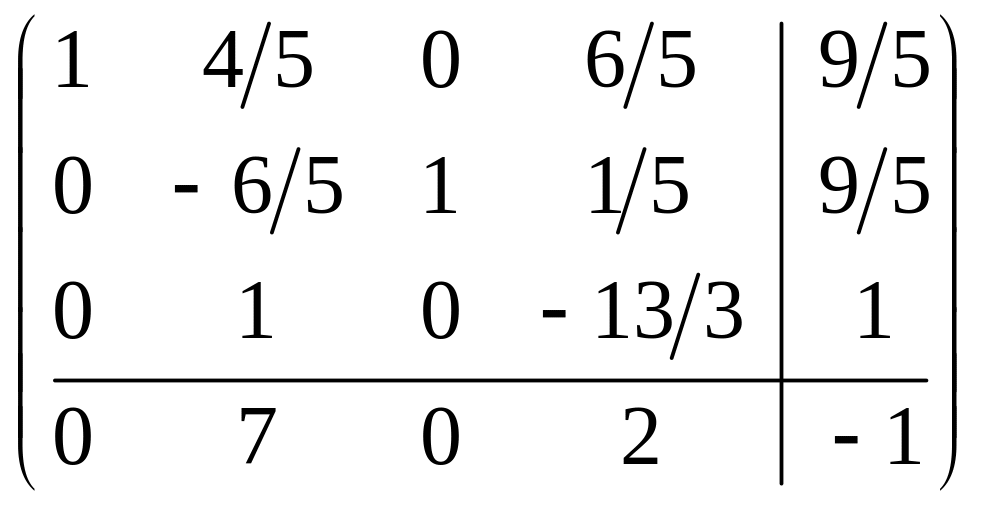
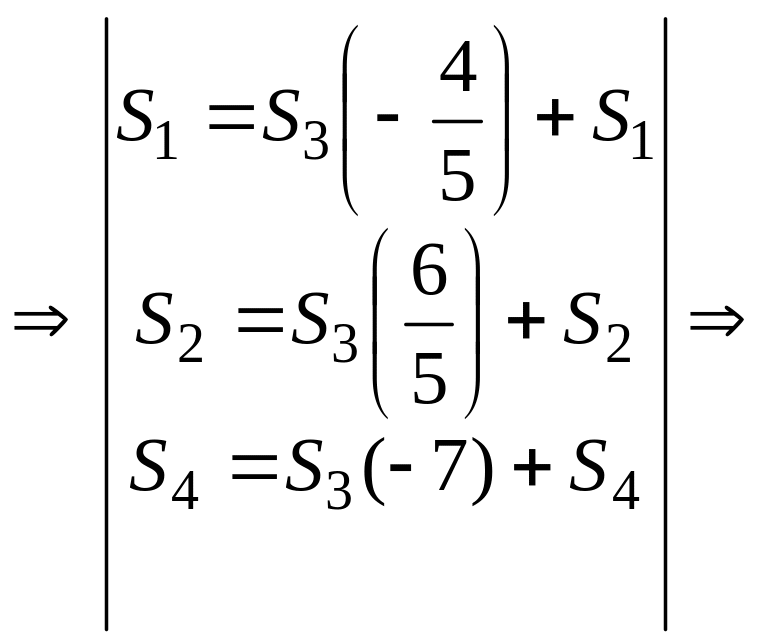
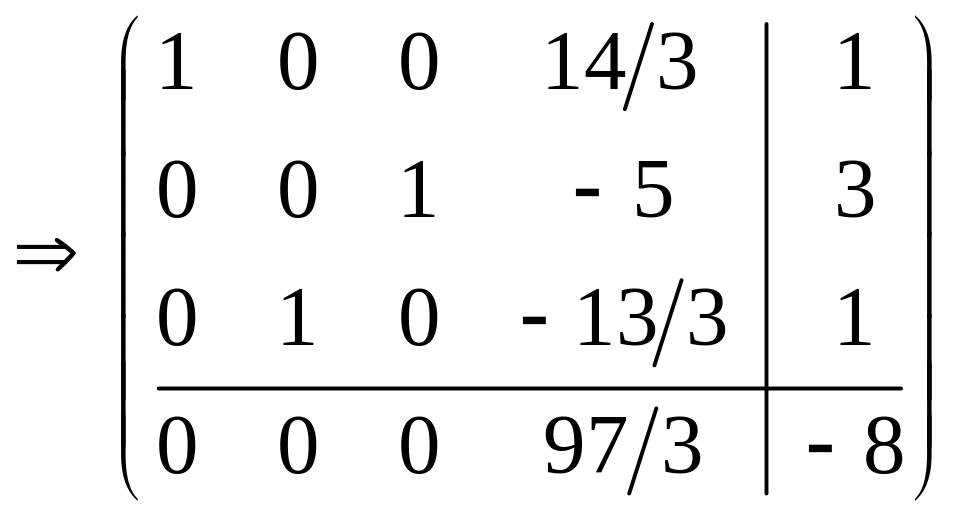 .
.
Таким
образом, получена правильная форма со
свободной переменной
![]() и базисными переменными
и базисными переменными
![]() ,
,
,
,
![]() .
Начальный допустимый план
.
Начальный допустимый план
![]() ,
значение целевой функции
,
значение целевой функции
![]() .
.
Проверим вычисления, найдя значения исходной целевой функции
![]()
![]() .
.
