Представление Денавита – Хартенберга

Для описания вращательных и поступательных связей между соседними звеньями Денавит и Хартенберг предложили матричный метод последовательного построения систем координат, связанных с каждым звеном кинематической цепи. Смысл представления Денавита–Хартенберга (ДХ-представление) состоит в формировании однородной матрицы преобразования, имеющей размерность 4×4 и описывающей положение системы координат каждого звена относительно системы координат предыдущего звена. Это дает возможность последовательно преобразовать координаты схвата манипулятора из системы отсчета, связанной с последним звеном, в базовую систему отсчета, являющейся инерциальной системой координат для рассматриваемой динамической системы.

Каждая система координат формируется на основе следующих трех правил:

1) ось z_i-1направлена вдоль оси i–го сочленения;

2) ось x_i перпендикулярна оси z_i-1 и направлена от нее;

3) ось y_i дополняет оси x_i, z_i до правой декартовой системы координат.

ДХ–представление твердых звеньев зависит от четырех геометрических параметров, соответствующих каждому звену. Эти четыре параметра полностью описывают любое вращательное или поступательное движение и определяются в соответствии с рис. 5.4 следующим образом:

_i – присоединенный угол, на который надо повернуть ось x_i-1вокруг оси z_i-1, чтобы она стала сонаправлена с осью x_i (знак определяется в соответствии с правилом правой руки);

d_i - расстояние между пересечением оси z_i-1 с осью x_i и началом (i-1)-й системы координат, отсчитываемое вдоль оси z_i-1 ;

a_i - линейное смещение – расстояние между пересечением оси z_i-1 с осью x_i и началом i-й системы координат, отсчитываемое вдоль оси x_i, т. е. кратчайшее расстояние между осями z_i-1 и z_i;

α_i - угловое смещение - угол, на который надо повернуть ось z_i-1 вокруг оси x_i, чтобы она стала сонаправленной с осью z_i (знак определяется в соответствии с правилом правой руки).

Для вращательных сочленений параметры d_i, a_i и α_i являются характеристикамисочленения, постоянными для данного типа робота. В то же время _i является переменной величиной, изменяющейся при движении (вращении) i-го звена относительно (i-1)-го.

Алгоритм формирования систем координат звеньев

Для каждого звена манипулятора с n степенями свободы этот алгоритм формирует ортонормированную систему координат. Системы координат нумеруются в порядке возрастания от основания к схвату манипулятора. Взаимное расположение соседних звеньев описывается однородной матрицей преобразования размерностью 4х4.

Параметры систем координат звеньев манипулятора Пума
Сочленение i					Пределы измерения
1	90	-90	0	0	-160-+160
2	0	0	431,8 мм	149,09 мм	-225-45
3	90	90	-20,32 мм	0	-45-225
4	0	-90	0	433,07 мм	-110-170
5	0	90	0	0	-100-100
6	0	0	0	56,25 мм	-266-266

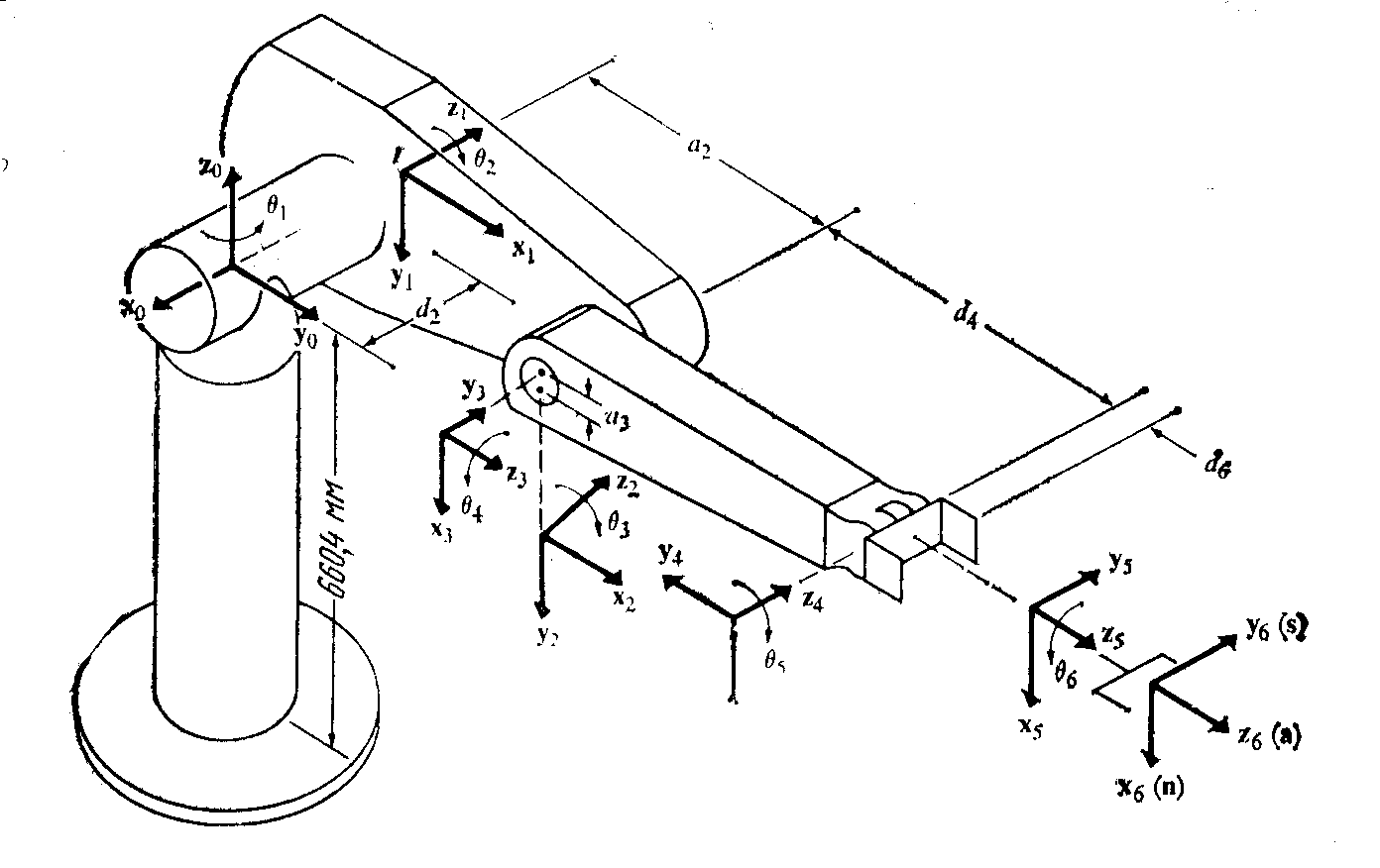
Рисунок 5.4. Формирование систем координат звеньев

Для манипулятора Пума

Шаг 1. Формирование базовой системы координат.

Сформировать правую ортонормированную систему координат (х₀, y₀, z₀), связанную с основанием, ось z₀ вдоль оси 1-го сочленения к «плечу» манипулятора. Оси х₀ и y₀ выбираются произвольно при условии их перпендикулярности оси z₀.

Шаг 2. Начало и цикл. Для всех i ( i=1,2 … n-1) выполнить шаги 3-6.

Шаг 3. Формирование осей сочленения. Направить ось z_i вдоль оси движения (вращательного или поступательного) i+1-го сочленения.

Шаг 4. Формирование начала i-й системы координат. Расположить начало i-й системы координат на пересечении осей z_i и z_i-1 или на пересечении общей нормали к осям z_i и z_i-1 с осью z_i.

Шаг 5. Формирование оси x_i. Выбрать единичный вектор x_i следующим образом: x_i = ±( z_i-1 × z_i)/ || z_i-1 × z_i || или вдоль общего перпендикуляра к осям z_i-1 и z_i, если они параллельны.

Шаг 6. Формирование оси y_i Положить y_i = +( z_i × x_i)/ ||z_i ×x_i|| , получив тем самым правостороннюю систему координат.

Шаг 7. Формирование системы координат схвата. Как правило, n-е сочленение является вращательным. Сформировать ось z_n, направив ее вдоль оси z_n-1 и от робота. Выбрать ось х_n так, чтобы она была перпендикулярна осям z_n-1 и z_n.

Шаг 8. Определение параметров звеньев и сочленений. Для каждого i

(i =1…n) выполнить шаги 9-12.

Шаг 9. Определение d_i Расстояние d_i – от начала (i-1)-й системы координат до пересечения оси z_i-1 с осью x_i и началом i-й системы координат, отсчитываемой вдоль оси z_i-1. Если i-е соединение – поступательное, то d_i – присоединенная переменная.

Шаг 10. Определение a_i - расстояния между пересечением оси z_i-1 с осью x_i и началом i-й системы координат, отсчитываемой вдоль оси x_i.

Шаг 11. Определение _i – угла поворота оси x_{i -1} вокруг оси z_i-1, чтобы она стала сонаправлена с осью x_i. Если i-е сочленение – вращательное, то _i-присоединенная переменная.

Шаг 12. Определение α_i – угла поворота оси z_{i -1} вокруг оси x_i, чтобы она стала сонаправлена с осью z_i .

После построения ДХ-координат для всех звеньев можно построить однородные матрицы преобразования, связывающие i-ю и (i-1)-ю системы координат:

^i-1A_i= T_z,dT_z,T_x,aT_x,α=×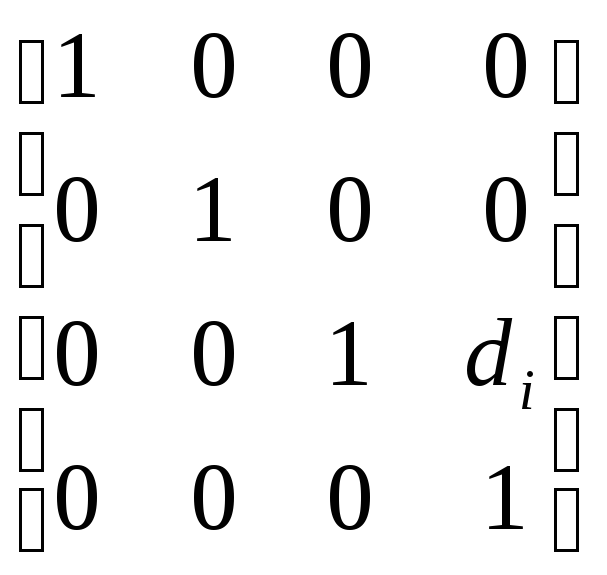

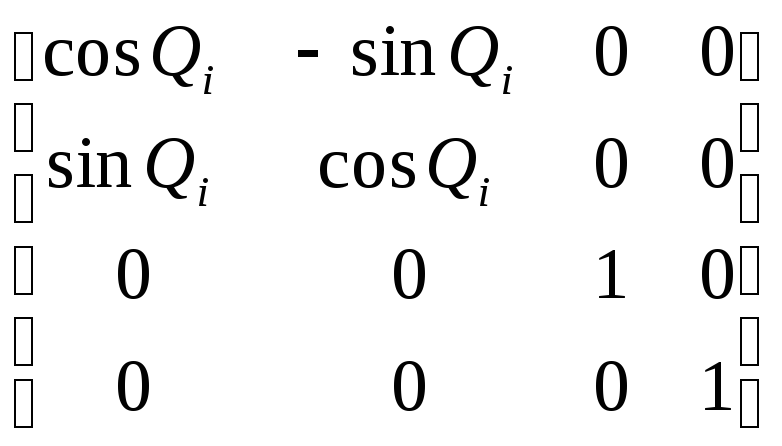
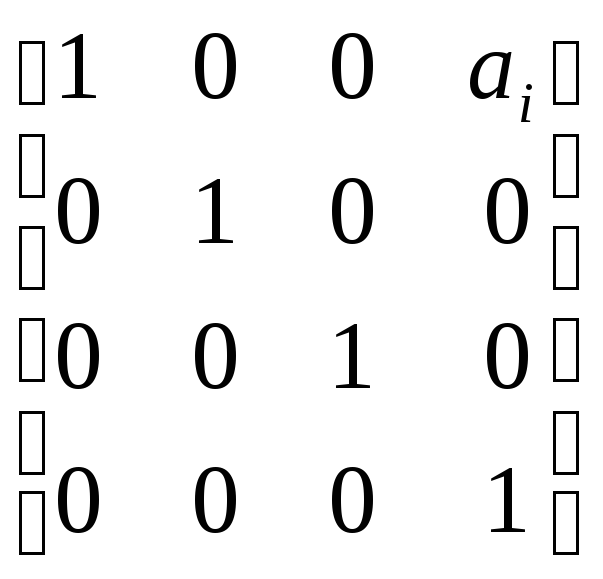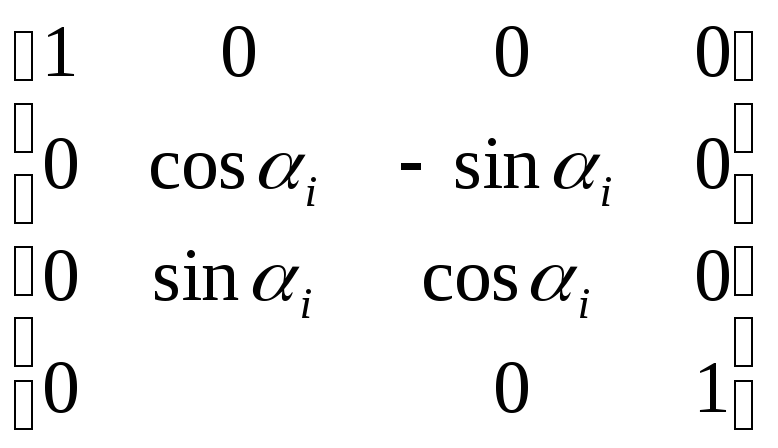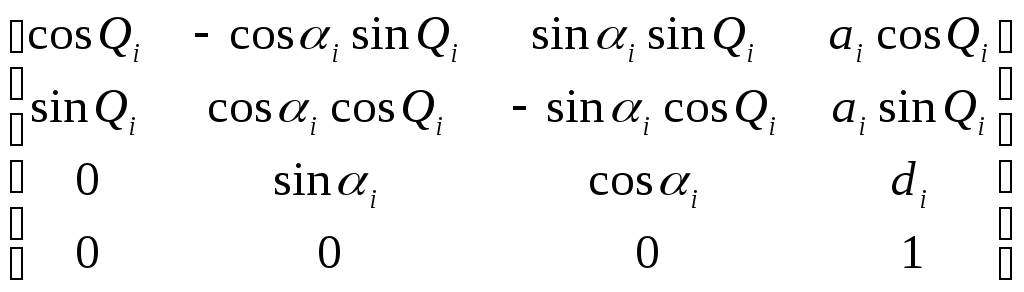×=. (5-1)

Преобразуя (3-1), найдем, что матрица, обратная к ^i-1А_i, имеет вид:

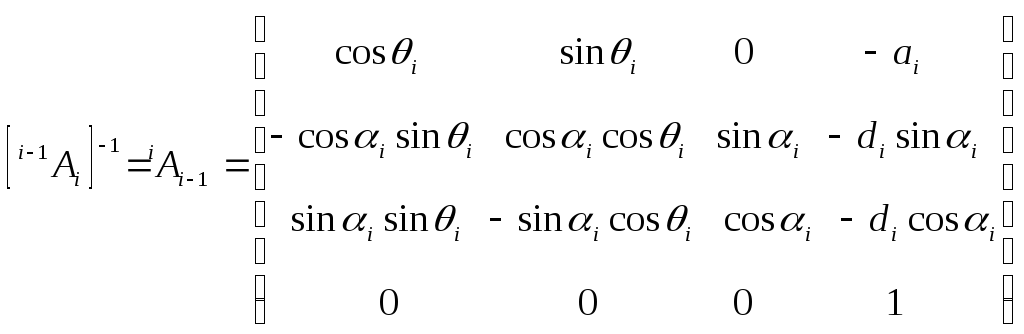, (5-2)

где - константы, а- присоединенная переменная, если рассматриваемое сочленение – вращательное.

Используя матрицу , можно связать однородные координатыр_i точки р относительно i-й системы координат (точка р покоится в i–й системе координат)с односторонними координатами этой точки относительно (i-1)-й системы тсчета, связанной с (i-1)-м звеном. Эта связь устанавливается равенством:

, (5-3)

где и.

Для шестизвенного манипулятора Пума были определены шесть матриц , соответствующие показанным на рис. 5.4. системам координат. Эти матрицы представлены ниже:

,

, ,

,

, ,

,

,

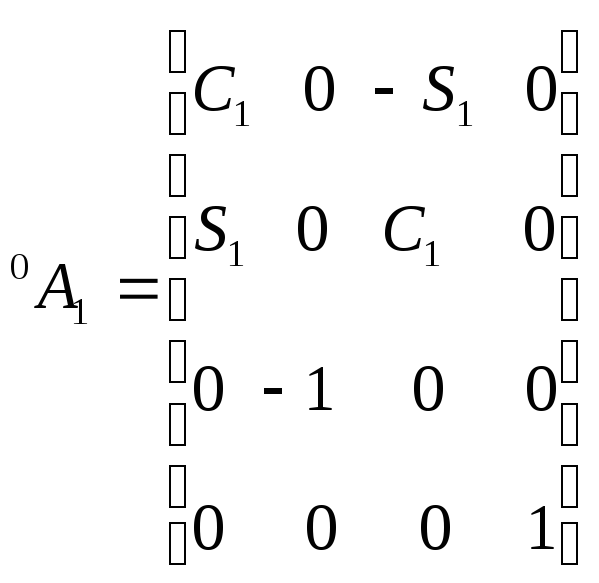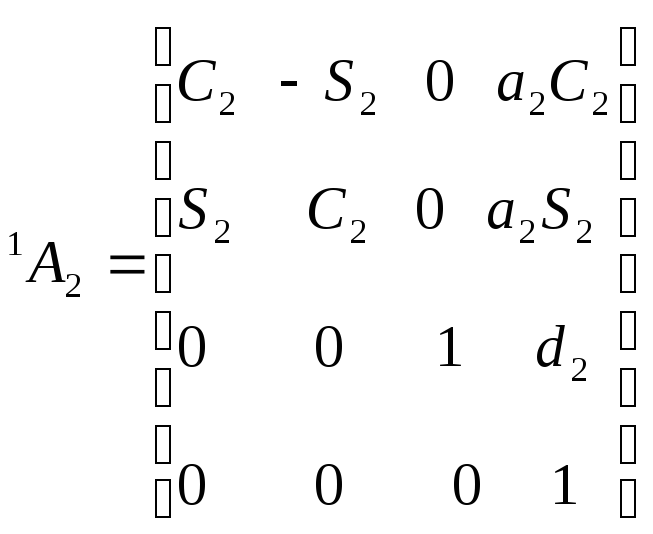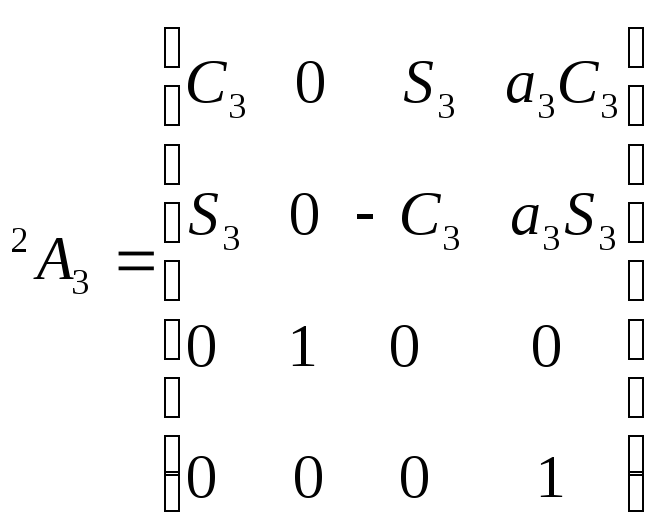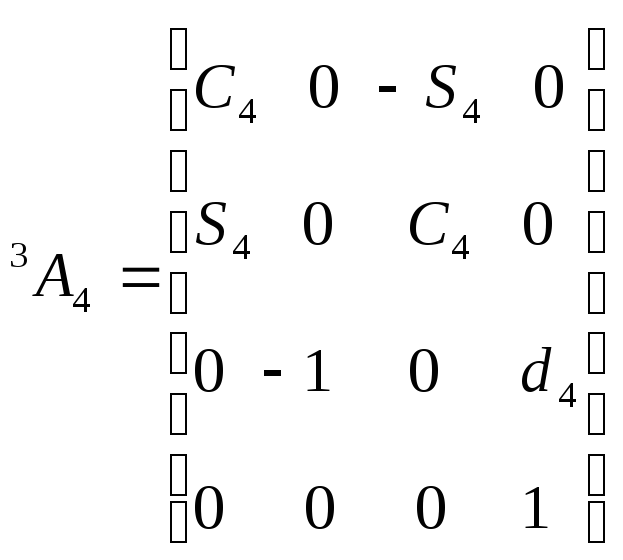
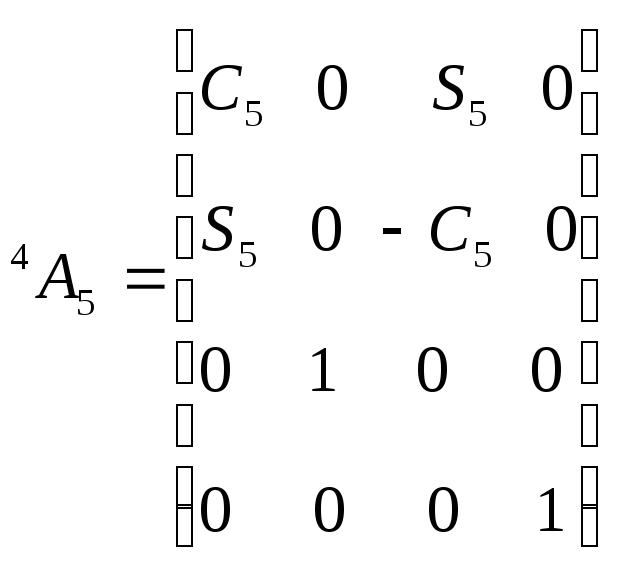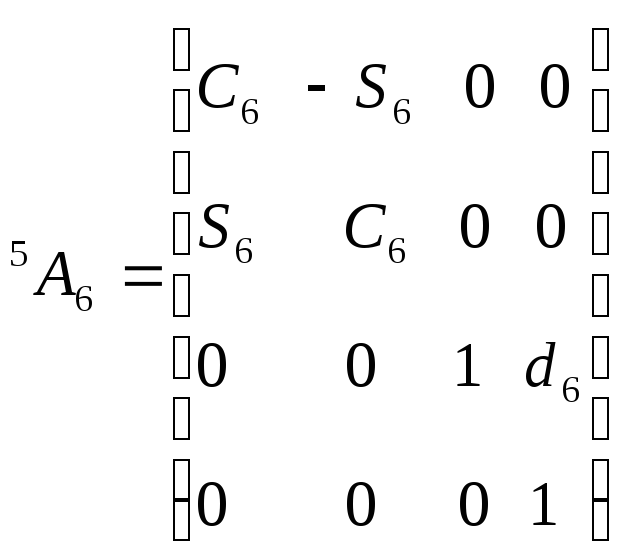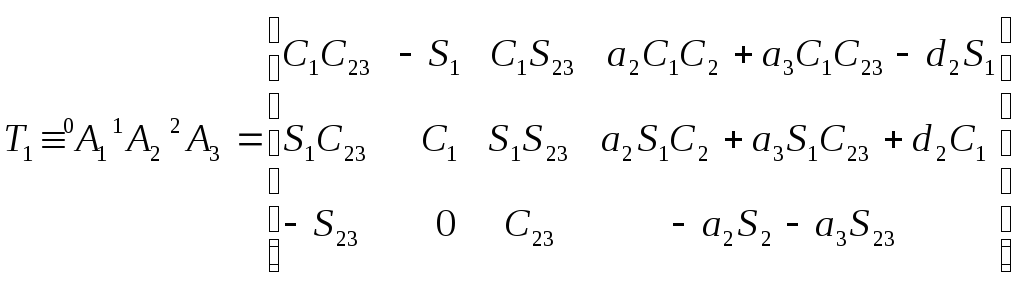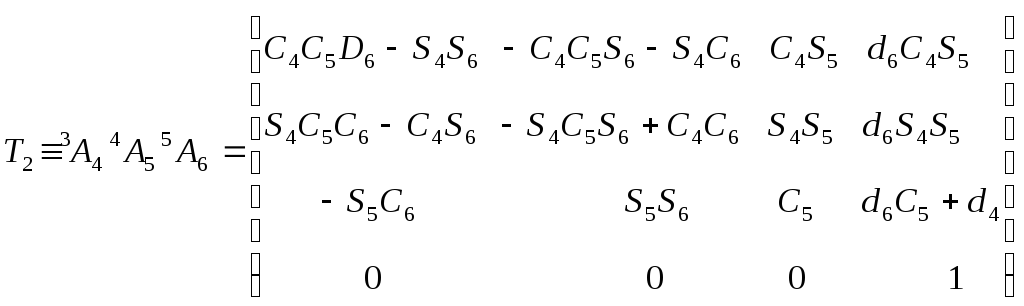где

; ;;.