11

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ ИМ. Н. Э. БАУМАНА

Факультет «ИНФОРМАТИКА И СИСТЕМЫ УПРАВЛЕНИЯ»

Кафедра ИУ-3

Методические указания к лабораторной работе №2 по курсу

«Цифровая обработка сигналов»

НЕПРЕРЫВНЫЙ ФИЛЬТР БОРЬБЫ С ЗЕРКАЛЬНЫМИ ПОМЕХАМИ

Составил доц. Герман Д. Я.

2009 г.

Лабораторная работа посвящена методике определения основных параметров непрерывного фильтра борьбы с зеркальными частотами.

Известно, что спектр непрерывного сигнала после дискретизации сигнала по времени с интервалом становится периодическим с периодом по частоте . Возникают так называемые зеркальные повторения «горбов» спектра. Если бы спектр непрерывного сигнала лежал в ограниченной области частот , то интервал дискретизации следовало бы выбрать равным

(1)

Тогда периодически повторяющиеся части спектра не перекрывались бы и искажения спектра в полосе частот не происходило.

Этому мешают две причины

1

. Спектры физически реализуемых объектов не ограничены четкими частотными границами и имеют бесконечные пределы. При очень больших частотах спектр может быть очень малой, но не равной нулю величиной. Поэтому «хвосты» периодически повторяющихся спектров накладываются друг на друга, складываются, и высокочастотные части сигнала искажаются. (См. рис. 1.)

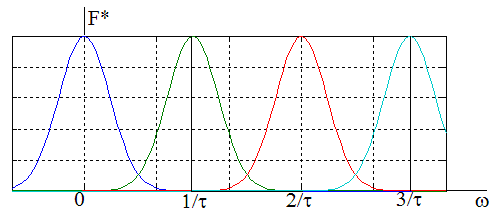
Рис. 1 Наложение «хвостов» спектра.

2. Спектр непрерывного сигнала может быть засорен помехами, лежащими вне области . Однако периодическое повторение спектра может привести к тому, что помеха, связанная с какой-то зеркальной частотой попадет внутрь рабочей области .

П

оэтому принимается следующее техническое решение. Перед дискретизацией непрерывный сигнал фильтруется непрерывным фильтром низкой частоты ФНЧ с частотой среза, равной .

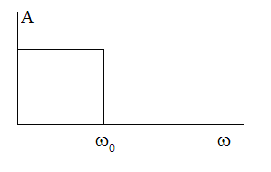
Рис. 2. Фильтр низкой частоты.

Это решение уменьшает обе вышеуказанные причины возникновения ошибок, но добавляет третью. ФНЧ отсекает высокочастотную часть спектра сигнала, не пропускает её на дальнейшую обработку и вносит ошибку в высокочастотную часть. Однако, эта причина менее опасна, чем первые две. Лабораторная работа посвящена выбору таких параметров ФНЧ, которые минимизировали бы ошибку обработки непрерывного сигнала фильтром борьбы с зеркальными частотами.

1. Проектирование непрерывного фильтра

Проектирование непрерывного фильтра возможно в рабочей области пакета MATLAB как это будет проделано в настоящей работе, так и в приложении SIMULINK как это предполагается в последующей лабораторной работе. В MATLABE предусмотрено проектирование следующих типов непрерывных фильтров:

1. Фильтр Баттерворта,

2. Фильтр Чебышева 1-го рода,

3. Фильтр Чебышева 2-го рода,

4. Эллиптический фильтр,

5. Фильтр Бесселя.

Это фильтры, у которых числитель и знаменатель передаточной функции представляют собой полиномы частоты. В начале проектирования рекомендуется выбрать порядок фильтра – порядок полинома знаменателя, и частоту среза. Это выполняется для одного из выбранных фильтров с помощью одной из перечисленных ниже команд (проектируется фильтр низкой частоты).

(2)

Здесь

- вычисленный порядок фильтра,

- вычисленная частота среза,

- заданная частота полосы пропускания (здесь и далее см. рис. 3),

- заданная частота полосы задерживания,

- заданный уровень пульсации в полосе пропускания,

- заданный уровень пульсации в полосе задерживания,

- признак расчета непрерывного фильтра.

Частоты измеряются в долях частоты Найквиста и должны находится в диапазоне от нуля до единицы. Уровни пульсации измеряются в децибелах.

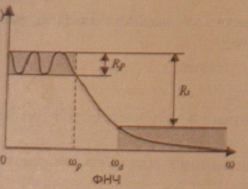
Рис. 3. Характеристики ФНЧ

Частота среза здесь вычисляется по заданным границам переходной полосы. Для фильтров, у которых отсутствует пульсация (см. полосу задерживания на рис. 3), граница переходной полосы определяется моментом входа АЧХ в коридор заданного уровня пульсации.

После определения порядка фильтра вычисляются коэффициенты передаточной функции для выбранного типа фильтра

(3)

На рис. 4 в логарифмическом масштабе представлен график АЧХ эллиптического фильтра, рассчитанного для параметров . График строился по командам (4).

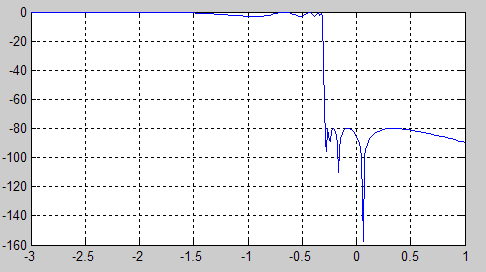
Рис. 4. АЧХ эллиптического фильтра в относительном масштабе частот.

Однако, в формулах (3) можно использовать реальные значения частоты среза, используя формулы (2) для определения порядка фильтра. На рис. 5 представлен АЧХ эллиптического фильтра, построенного для прежних исходных данных за исключением

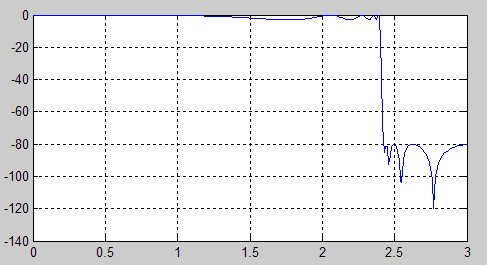
Рис. 5. АЧХ эллиптического фильтра в реальном масштабе частот.

Задание к разделу 1.

1 Построить АЧХ каждого из четырех типов фильтров.

После команд (2)-(3) для построения АЧХ рекомендуем использовать

(4)

2. Отметить, чем отличается каждый из типов фильтров.

3. Какой тип фильтра имеет самую узкую полосу перехода при сравнимых порядках фильтров.

2. Входной сигнал

В качестве входного сигнала выбираем экспоненту с постоянной времени, равной единице. Построим её

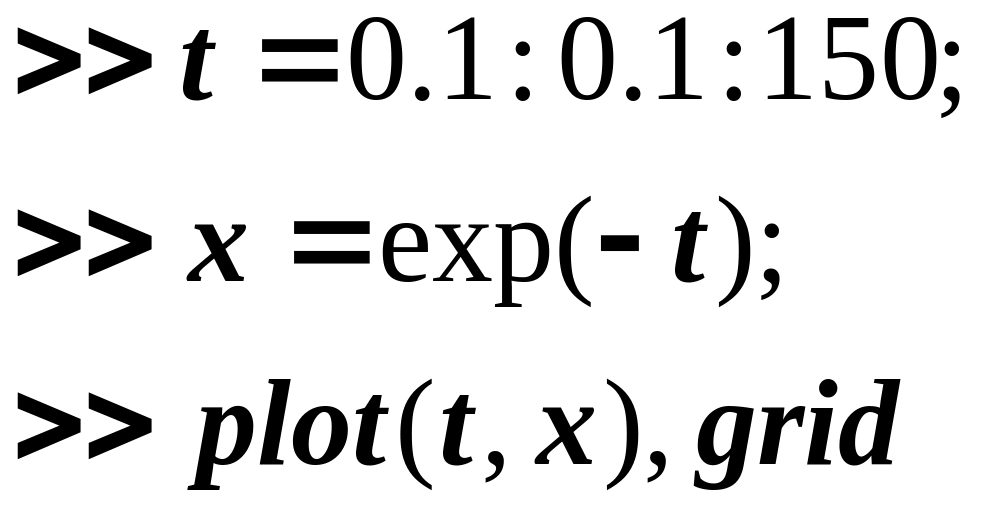(5)

Спектр сигнала можно получить как преобразование Фурье функцией . Однако в MATLABE мы можем получить только дискретную экспоненту. Тогда её спектр будет периодический. Это затруднит расчеты. Поэтому значение модуля спектра получим из справочника как преобразование Фурье для непрерывной экспоненты.

(6)

Задание к разделу 2.

1. Чему равна частота дискретизации у дискретной модели экспоненты (5)?

2. Постройте график модуля спектра. Предварительно оцените частоту среза

фильтра борьбы с зеркальными частотами. В конце лабораторной работы проверьте правильность своей оценки.