3.3. Основні властивості розв’язків задачі лінійного програмування

Властивості розв’язків задачі лінійного програмування формулюються у вигляді чотирьох теорем.

Властивість 1. (Теорема 3.1) Множина всіх планів задачі лінійного програмування опукла.

Властивість 2. (Теорема 3.2) Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатогранника розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.

Властивість 3. (Теорема 3.3) Якщо відомо, що система векторів A₁, A₂, …, A_k (k ≤ n) у розкладі A₁x₁ +A₂x₂ + … + A_nx_n = A₀, X ≥ 0 лінійно незалежна і така, що A₁x₁ + A₂x₂ + … + A_kx_k = A₀, де всі x_j ≥ 0, то точка X = (x₁, x₂, …, x_k, 0, …, 0) є кутовою точкою багатогранника розв’язків.

Властивість 4. (Теорема 3.4) Якщо X = (x₁, x₂, …, x_n) — кутова точка багатогранника розв’язків, то вектори в розкладі A₁x₁ + + A₂x₂ + … + A_nx_n = A₀, X ≥ 0, що відповідають додатним x_j, є лінійно незалежними.

3.3. Графічний метод розв’язування задач лінійного програмування

Для розв’язування двовимірних задач лінійного програмування, тобто задач із двома змінними, а також деяких тривимірних задач застосовують графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування. Обмежене використання графічного методу зумовлене складністю побудови багатогранника розв’язків у тривимірному просторі (для задач з трьома змінними), а графічне зображення задачі з кількістю змінних більше трьох взагалі неможливе.

Розглянемо задачу.

Знайти

(3.10)

за умов:

(3.11)

. (3.12)

Припустимо, що система (3.11) за умов (3.12) сумісна і багатокутник її розв’язків обмежений.

Згідно з геометричною інтерпретацією задачі лінійного програмування кожне і-те обмеження-нерівність у (3.11) визначає півплощину з граничною прямою (і = 1, 2, …, т). Системою обмежень (3.11) графічно можна зобразити спільну частину, або переріз усіх зазначених півплощин, тобто множину точок, координати яких задовольняють всі обмеження задачі — багатокутник розв’язків.

Умова (3.12) невід’ємності змінних означає, що область допустимих розв’язків задачі належить першому квадранту системи координат двовимірного простору. Цільова функція задачі лінійного програмування геометрично інтерпретується як сім’я паралельних прямих с₁х₁ + с₂х₂ = const.

Скористаємося для графічного розв’язання задачі лінійного програмування властивостями які можна сформулювати так: якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатокутника розв’язків. Якщо ж цільова функція досягає екстремального значення більш як в одній вершині багатокутника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією цих вершин.

Отже, розв’язати задачу лінійного програмування графічно означає знайти таку вершину багатокутника розв’язків, у результаті підстановки координат якої в (3.10) лінійна цільова функція набуває найбільшого (найменшого) значення.

Алгоритм графічного методу розв’язування задачі лінійного програмування складається з таких кроків:

1. Будуємо прямі, якіє межами півплощин - нерівностей системи, рівняння яких дістаємо заміною в обмеженнях задачі (3.11) знаків нерівностей на знаки рівностей.

2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.

3. Знаходимо багатокутник розв’язків задачі лінійного програмування.

4. Будуємо вектор , що задає напрям зростання значення цільової функції задачі.

5. Будуємо пряму с₁х₁ + с₂х₂ = const, перпендикулярну до вектора .

6. Переміщуючи пряму с₁х₁ + с₂х₂ = const в напрямку вектора (для задачі на maxZ) або в протилежному напрямі (для задачі на minZ), знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального значення.

7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.

Приклад 3.2. Деяке виробниче підприємство спеціалізується на виробництві двох видів продукції — А та В. На виготовлення продукції використовується два види сировини 1 та 2. Норми витрат сировини кожного виду і прибуток фірми від реалізації одиниці продукції подано в табл.3.1.

Таблиця 3.1.

Сировина	Норми витрат сировини на одиницю продукції		Виробничий запас сировини
	А	В
1	3	5	450
2	4	2	280
Прибуток	10	8

Відомо, що тижневий попит на на продукцію типу А перевищує попит на продукцію В не більш як на 10 одиниць, а продаж продукції типу В не перевищує 70 одиниць на тиждень.

Необхідно визначити такі тижневі обсяги виробництва продукції двох типів, що максимізують прибуток фірми.

Побудуємо економіко-математичну модель задачі та розв’яжемо її графічно.

Побудова математичної моделі. Позначимо х₁ — кількість продукції типу А, виготовлених фірмою за тиждень, а х₂ — кількість продукції типу В. Цільова функція задачі — максимум прибутку фірми від реалізації продукції:

.

Обмеження задачі враховують норми витрат сировини 1 та 2 для виготовлення продукції та попит на продукцію:

Загалом економіко-математичну модель цієї задачі можна записати так:

Z = 10х₁ + 8х₂ →max

за умов:

Маємо загальну економіко-математичну модель, що є моделлю ЗЛП, що містить лише дві змінні, і тому може бути розв’язана графічно.

Розв’язання. Перший крок згідно з графічним методом полягає в геометричному зображенні допустимих планів задачі, тобто у визначенні такої області, де водночас виконуються всі обмеження моделі. Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рис. 3.2.). Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї з півплощин задовольняють розглядувану нерівність, а іншої — ні. Щоб визначити необхідну півплощину (на рис. 3.2. її напрям позначено стрілкою), потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. Інакше таким зображенням є інша півплощина.

Умова невід’ємності змінних х₁ ≥ 0, х₂ ≥ 0 обмежує область допустимих планів задачі першим квадрантом системи координат. Переріз усіх півплощин визначає область допустимих планів задачі — шестикутник OABCDE. Координати будь-якої його точки задовольняють систему обмежень задачі та умову невід’ємності змінних. Тому поставлену задачу буде розв’язано, якщо ми зможемо відшукати таку точку багатокутника OABCDE, в якій цільова функція Z набирає найбільшого значення.

Для цього побудуємо вектор , координатами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор завжди виходить із початку координат і напрямлений до точки з координатами (х₁ = с₁; х₂ = с₂). У нашій задачі вектор . Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.

Побудуємо лінію, що відповідає, наприклад, значенню Z = 0. Це буде пряма 10х₁ + 8х₂ = 0, яка перпендикулярна до вектора і проходить через початок координат. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо пряму 10х₁ + 8х₂ = 0 паралельно самій собі згідно з напрямом вектора доти, доки не визначимо останню спільну точку прямої і багатокутника розв’язків,що і відповідає оптимальному плану задачі.

Р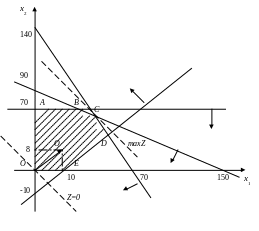 ис. 3.2

Із рис. 3.2. видно, що останньою спільною точкою прямої цільової функції та багатокутника OABCDE є точка С. Координати цієї точки є оптимальним планом задачі, тобто такими обсягами виробництва продукції видів А та В, що забезпечують максимум прибутку від їх реалізації за даних умов.

Координати точки С є розв’язком системи рівнянь :

звідси маємо: х₁ = 35,7; х₂ = 68,6.

Отже, Х^* = (36; 68);

Це означає, що коли фірма щотижня виготовлятиме 36 одиниць прдукції типу А та 68 — типу В, то вона отримає максимальний прибуток — 904 грошові одиниці. Це потребуватиме повного використання тижневих ресурсів сировини 1 та 2.

Рис.3.3 Рис.3.4

Рис.3.5 Рис.3.6

Розв’язувати графічним методом можна також задачі лінійного програмування n-вимірного простору, де , якщо при зведенні системи нерівностей задачі до системи рівнянь шляхом введення додаткових змінних кількість змінних n на дві більша, ніж число обмежень m, тобто .

Тоді, як відомо з курсу вищої математики, можна дві з n змінних, наприклад х₁ та х₂, вибрати як вільні, а інші m зробити базисними і виразити через вільні. Припустимо, що це зроблено. Отримаємо рівнянь вигляду:

(3.13)

Оскільки всі значення , то мають виконуватись умови: ,

(3.14)

Розглянемо, як можна відобразити ці умови геометрично. Візьмемо, наприклад, першу з них:

прирівнявши х₃ до нуля отримаємо рівняння:

.

Це рівняння прямої. Для такої прямої , по одну сторону від неї , а по другу — . Обираємо півплощину по ту сторону прямої , де . Аналогічним чином побудуємо решту граничних прямих: ; ;...; і знайдемо для кожної з них півплощину додатніх значень змінних. У такий спосіб отримують n–2 прямі та дві осі координат ( , ). Кожна з них визначає півплощину, де виконується умова . Перетин цих півплощин у площині утворює багатокутник допустимих розв’язківзадачі.

Припустимо, що в задачі необхідно знайти максимальне значення цільової фукції:

. (3.15)

Підставивши вирази для , , , ...; з (3.13) в (3.15), зведемо подібні доданки і отримаємо вираз для лінійної n –вимірної функції F лише через дві вільні змінні та :

,

де — вільний член, якого в початковому вигляді функція F не мала.

Очевидно, що лінійна функція досягає свого максимального значення за тих самих значень та , що й . Отже, процедура відшукання оптимального плану з множини допустимих далі здійснюється за алгоритмом для випадку двох змінних.

Необхідно зазначити, що графічний метод для визначення оптимального плану ЗЛП, все ж таки, доцільно застосовувати лише для задач із двома змінними. Для задач, що містять більш ніж дві змінні необхідно застосовувати інший метод. З властивостей розв’язків задачі лінійного програмування відомо: оптимальний розв’язок задачі має знаходитись в одній з кутових точок – вершин багатогранника розв’язків. Тому найпростіший спосіб відшукання оптимального плану потребує перебору всіх кутових точок – вершин багатогранника розв’язків. Крім того, кожний опорний план задачі визначається системою m лінійно незалежних векторів, серед n векторів системи обмежень задачі - . Отже, загальна кількість опорних планів – вершин багатокутника розв’язків дорівнює кількості комбінацій .

Задачі, що описують реальні економічні процеси, є задачами великої розмірності тому навіть простий перебір всіх опорних планів таких задач буде не простим, навіть за умови застосування сучасних ЕОМ. Тому існує необхідність застосування алгоритму, який би скорочував кількість однотипних обчислень. Таких алгоритмів було запропоновано математиками багато, але найбільш ефективним серед них є алгоритм відомий під назвою симплексний метод, або метод послідовного покращення опорного плану задачі. Ідея цього методу була розроблена російським вченим – математиком Л.В. Кантовичем, ще у 1939 році, алгоритм практичного застосування ідеї Кантовича був представлений американським вченим Дж.Данцігом у 1949 році.