2. Лабораторная установка для записи волоконных брэгговских решеток в схеме с интерферометром Ллойда.

В силу малого периода брэгговских решеток (  0.5 мкм) их, как правило, формируют с использованием интерференционных методов, Рис.2. Так как процесс записи необходимой решеточной структуры может длиться несколько десятков минут, изготовление качественной решетки возможно лишь при высокой стабильности интерференционной картины. Несмотря на то, что число предложенных схем записи решеток довольно велико, наибольшее распространение получил метод использующий интерферометр Ллойда, Рис. 2(б).

Период записываемой решётки рассчитывается по следующей формуле:

Λ = λ_UV /2sin(α/2) (11)

где λ_UV – длина волны записывающего излучения

Рис. 2. Оптическая схема лабораторной установки для записи волоконных брэгговских решеток. Схемы записи брэгговских решеток в интерферометрах с амплитудным (а) и пространственным (б) разделением пучка УФ-излучения

Длина волны брэгговского резонанса λ_Br при распространении света по волокну

λ_Br = n_eff λ_UV /sin(α/2) (12)

где n_eff – эффективный показатель преломления фундаментальной моды.

Для экспериментального определения используются измерения спектров отражения и пропускания волоконных брэгговских решёток, при этом используются волонные циркуляторы, стандартные спектроанализаторы ИК-диапазона и широкополосные источники ИК излучения: дискретные (рис.3) или непрерывные (например, суперлюминесцентные диоды).

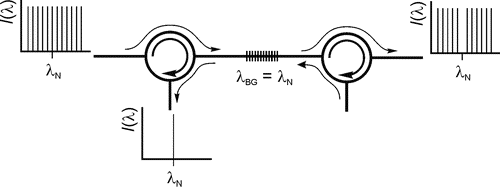
Рис. 3. Схема регистрации спектров отражения и пропускания волоконных решеток.

3. Примеры исследования спектральных свойств брэгговских решеток.

Спектральные характеристики однородных решеток с низким (r_max ≈ 13,1%) и высоким (r_max ≈ 99,997 %) коэффициентами отражения приведены на рис. 4а и б. Амплитуда модуляции показателя преломления была Δn_mod = 5*10^-5 и 7,5*10^-4, при этом сдвиг резонансной длины волны относительно λ = 1500 нм составил Δλ ≈ 0,037 нм и 0,58 нм соответственно. Спектральная ширина основного пика отражения на полувысоте для случая решетки с высоким коэффициентом отражения (см. рис. 4б) составила Δλ_FWHM ≈ 0,64 нм, что, как и следует из формулы (10), существенно больше спектральной ширины решетки с низким коэффициентом отражения Δλ_FWHM ≈ 0,15 нм. В спектре однородной брэгговской решетки с высоким коэффициентом отражения присутствует интенсивные боковые максимумы, наличие которых нежелательно в ряде практических применений. Для подавления этих максимумов обычно применяют специальное профилирование наведенного показателя преломления по длине решетки (apodization). Так использование гауссовой огибающей профиля наведенного показателя преломления в решетке позволяет подавить боковые максимумы с длинноволновой стороны от основного резонанса. Наличие нескольких боковых максимумов с коротковолновой стороны вызвано изменением среднего наведенного показателя преломления Δn_avr(z) вдоль решетки, что в соответствии с (4) приводит к изменению резонансной длины волны λ_Br(z) и интерференции излучения, отраженного от различных частей решетки.

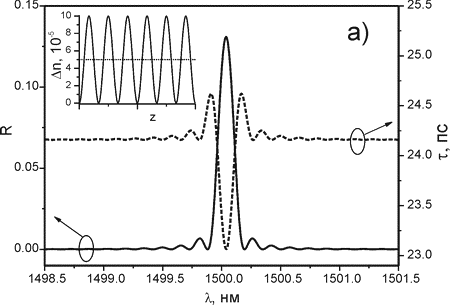
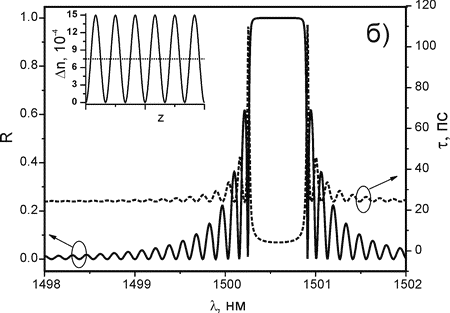
Рис. 4. Спектр отражения R [сплошная кривая] и групповая задержка τ [штриховая кривая] однородных брэгговских решеток с различной амплитудой модуляции наведенного ПП: n_mod = 5·10^-5 (а), n_mod = 7.5·10^-4 (б). На вставках: схематический профиль показателя преломления, наведенного в решетках.

Групповая задержка для фундаментальной моды определяется как:

τ = L/(c/n_eff) (23)

В случае рассмотренных на рис. 4 решеток эта задержка составила τ₀ = 24,15 пс. В области резонансного пика отражения и его боковых максимумов возникают отклонения групповой задержки от значения τ₀, величина и спектральное распределение которых сильно зависят от структуры решетки (рис. 4). Для компенсации дисперсии в современных волоконно-оптических линиях связи значительный интерес представляют решетки, резонансная длина волны которых заданным образом меняется вдоль их длины (chirped grating). Такие решетки могут быть созданы путем изменения периода или эффективного показателя преломления основной моды (см. уравнение (4)).