
- •Теорія ймовірностей`
- •1. Скінченний та зліченний імовірносний простір. Геометричне визначення імовірності
- •1.2. Події та операції над подіями
- •1.3. Скінченний простір елементарних подій
- •1.4. Зліченна ймовірносна схема
- •1.5. Геометричне визначення ймовірності
- •2. Аксіоматика теорії ймовірностей
- •2.1. Поняття ймовірносного простору. Властивості ймовірності
- •2.2. Умовні ймовірності. Незалежність подій
- •2.3. Формула повної ймовірності і формула Байєса
- •3. Дискретні випадкові величини
- •3.1. Поняття дискретної випадкової величини
- •3.2. Закон розподілу дискретної випадкової величини
- •3.3. Математичне сподівання
- •3.4. Багатовимірні закони розподілу
- •3.5. Додаткові властивості математичного сподівання і дисперсії
- •3.6. Коваріація та коефіцієнт кореляції
- •3.7. Нерівність Чебишова і закон великих чисел
- •3.8. Генератриси цілочислових випадкових величин
- •3.9. Багатовимірні генератриси
- •3.10. Гіллясті процеси
- •3.11. Слабка збіжність випадкових величин
- •3.12. Граничні теореми в схемі Бернуллі
- •4. Випадкові величини загального типу
- •4.1. Визначення випадкової величини. Її функція розподілу
- •4.2. Розподіл ймовірностей випадкової величини. Вибірковий ймовірносний простір
- •4.3. Дискретні, абсолютно неперервні і сингулярні розподіли
- •4.4. Функції від випадкових величин
- •4.5. Багатовимірні розподіли
- •4.6. Незалежність випадкових величин
- •4.7. Математичне сподівання
- •4.8. Теорема Лебега. Формули для обчислення математичного сподівання
- •4.9. Закон великих чисел і метод Монте-Карло
- •4.11. Характеристична функція. Її основні властивості
- •4.12. Формули обернення для характеристичних функцій
- •4.13. Неперервна відповідність між функціями розподілу і характеристичними функціями
- •4.14. Закон великих чисел у формі Хінчина
- •4.15. Центральна гранична теорема
2.2. Умовні ймовірності. Незалежність подій
Нехай проводиться n експериментів, nB - число експериментів, у яких відбулась подія B. Нехай серед nB експериментів разом з B подія A відбулась nAB разів. Частотою події A по відношенню до експериментів з наслідком B є відношення
![]() .
.
Ця
формула є підґрунтям наступного
визначення: якщо подія В
така, що
![]() ,
то умовна ймовірність події А
при умові, що відбулась
подія В,
дорівнює
,
то умовна ймовірність події А
при умові, що відбулась
подія В,
дорівнює
![]() . (2.1)
. (2.1)
Для умовної ймовірності Р(А/B) будемо також використовувати позначення РВ(А). При фіксованому В РВ(·) має усі властивості ймовірності:
РВ(А) 0;
РВ() = 1;
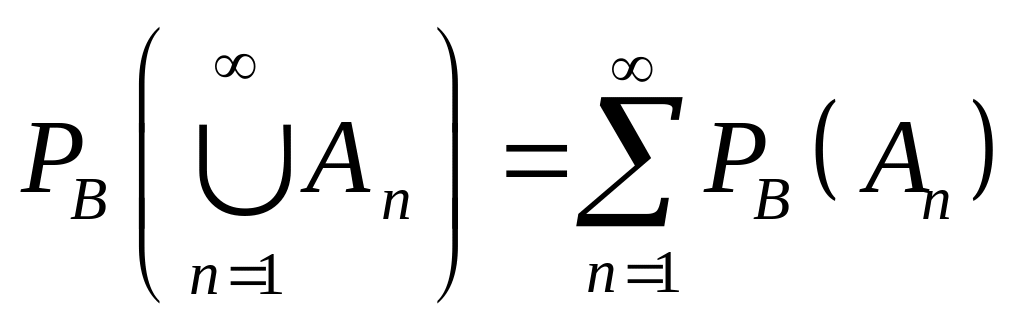 ,
якщо
,
якщо
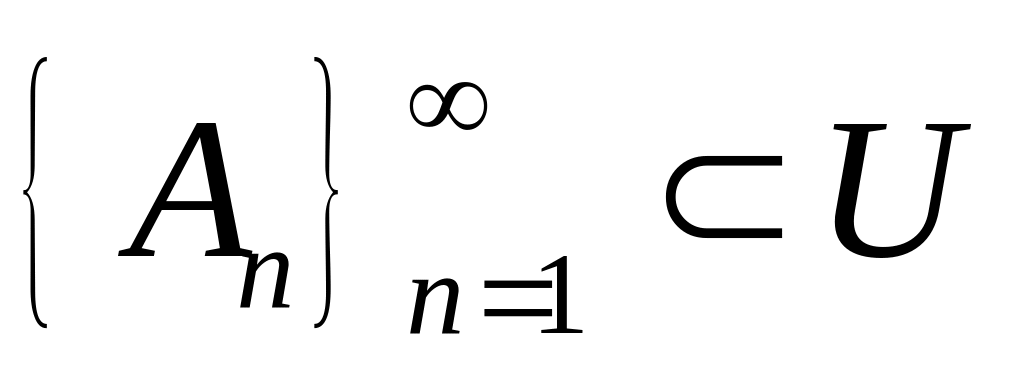 і
і
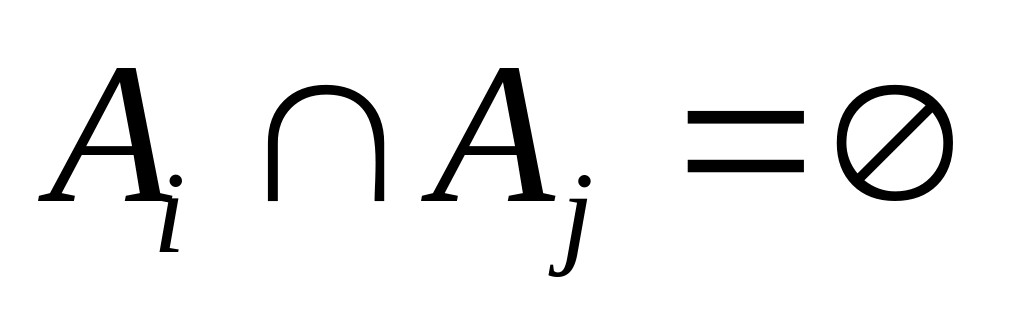 ,
.
,
.
Для РВ(·) = Р(·/В) також справедливі наслідки 2.1, 2.2 з аксіом.
Рівність (2.1) можна подати у вигляді
Р(А·В) = Р(В) Р(А/В). (2.2)
Методом математичної індукції неважко цю рівність узагальнити
Р(Ап Ап-1 .. А1)=Р(Ап/Ап-1...А1)Р(Ап-1/Ап-2...А1)...Р(А2/А1)Р(А1),
якщо Р( Ап-1... А1) 0.
Події
А і В будемо називати незалежними, якщо
![]() .
.
Розглянемо такий приклад. Нехай подія А полягає у тому, що навмання кинута у квадрат зі стороною 1 точка впала в область, що лежить вправо від абсциси а, подія В – у тому, що точка впала в область, що лежить вище ординати b. Очевидно, що P(A∙B)=P(A)·Р(В). Останнє співвідношення можна підтвердити наступним рисунком:
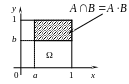
Властивості незалежних подій:
1.
Якщо
![]() ,
і
,
і
![]() ,
,
![]() – незалежні, тоді
– незалежні, тоді
![]() .
.
2.
Якщо А
і В
– незалежні, то незалежними
будуть
![]() і B, A
і
і B, A
і
![]() ,
і
(властивість
спадковості).
,
і
(властивість
спадковості).
Події
![]() незалежні у сукупності,
якщо для будь-яких індексів
незалежні у сукупності,
якщо для будь-яких індексів
![]()
![]() .
.
Приклад (С.Н. Бернштейн). Стохастичний експеримент полягає у тому, що на площину кидається тетраедр. Три грані тетраедра пофарбовані відповідно у червоний, синій і зелений колір, а на четверту нанесені усі три кольори. Нехай А – подія, яка полягає у тому, що при підкиданні тетраедра на площину впала грань, яка має червоний колір, подія В – синій колір, подія С – зелений колір. Треба дослідити систему подій А, В, С на незалежність.
Перевіримо, що А, В, С – попарно незалежні, але не є незалежними у сукупності. Дійсно,
![]() ,
,
![]() ,
,
![]() .
.
2.3. Формула повної ймовірності і формула Байєса
Важливу роль в теорії ймовірностей відіграє наступний результат.
Теорема
2.1 (формула
повної ймовірності).
Нехай для події A
існує послідовність подій Bi
, i = 1,2,…
таких, що BiBj =
для i j,
P(Bi) > 0
для i = 1,2,…
, і, крім того,
![]() Тоді
Тоді
![]() .
(2.3)
.
(2.3)
Теорема
2.2 (Формула Байєса).
Нехай
![]() - повна група подій і В
– деяка подія такі, що
- повна група подій і В
– деяка подія такі, що
![]() Тоді
Тоді
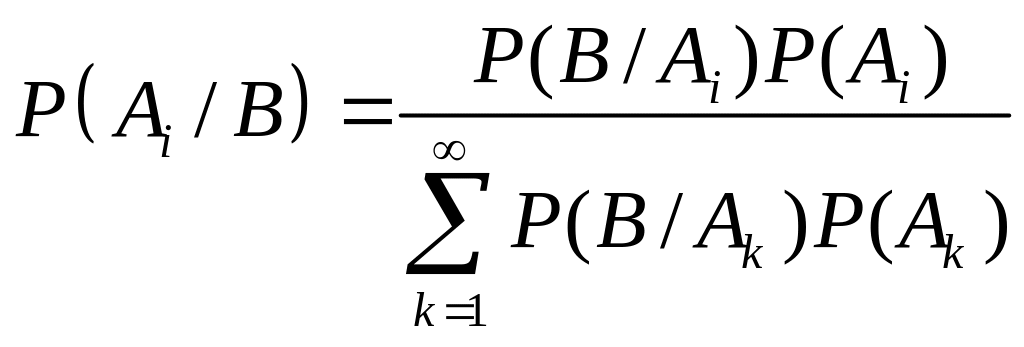 . (2.4)
. (2.4)
Формулі
Байєса можна дати наступну інтерпретацію.
Будемо називати події
![]() гіпотезами. Нехай подія В
– результат деякого експерименту.
Імовірність Р(Аі)
– це апріорні ймовірності гіпотез, які
підраховані до проведення експерименту.
Умовні ймовірності Р(Аі/В)
– це апостеріорні ймовірності гіпотез,
які підраховані після того, як став
відомим результат В.
Формула Байєса дозволяє за апріорними
ймовірностями і за умовними ймовірностями
події В при
гіпотезах Аі
підраховувати апостеріорні ймовірності.
гіпотезами. Нехай подія В
– результат деякого експерименту.
Імовірність Р(Аі)
– це апріорні ймовірності гіпотез, які
підраховані до проведення експерименту.
Умовні ймовірності Р(Аі/В)
– це апостеріорні ймовірності гіпотез,
які підраховані після того, як став
відомим результат В.
Формула Байєса дозволяє за апріорними
ймовірностями і за умовними ймовірностями
події В при
гіпотезах Аі
підраховувати апостеріорні ймовірності.
