4.9. Закон великих чисел і метод Монте-Карло

Так само, як і для дискретних випадкових величин, в загальному випадку визначаються: момент -го порядку, абсолютний момент -го порядку, центральний момент -го порядку, абсолютний центральний момент -го порядку. Як і раніше, центральний момент 2-го порядку називається дисперсією і, якщо , то справедлива нерівність Чебишова

, . (4.11)

На загальний випадок переноситься і закон великих чисел:

якщо - незалежні, однаково розподілені і , то

. (4.12)

Використаємо (4.12) для підрахунку інтегралів. Нехай нам необхідно обчислити інтеграл , де і .

Розглянемо випадковий вектор , який визначається своєю щільністю

а також випадкову величину . Тоді

.

Тепер, якщо ми візьмемо незалежні реалізації випадкової величини , то згідно закону великих чисел .

4.11. Характеристична функція. Її основні властивості

Характеристичною функцією випадкової величини ми будемо називати функцію від дійсного аргументу , яка дорівнює

.

Якщо має щільність розподілу , то

.

У випадку, коли розподіл дискретний .

Властивості характеристичної функції:

1) при кожному дійсному , .

2) рівномірно неперервна по .

3. Якщо , де і 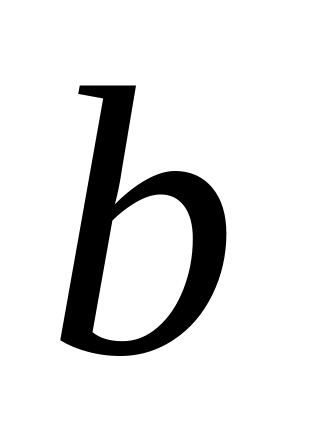константи, то

.

3. Якщо незалежні, то .

4. .

5. Позначимо . Якщо - скінченне, то існують усі похідні при і

. (4.16)

Крім того має місце такий розклад

, (4.17)

де при .

Обчислимо характеристичні функції для найбільш відомих розподілів.

1) Біноміальний розподіл.

.

.

2. Пуассонівський розподіл.

. .

2. Геометричний розподіл.

. .

2. Вироджений розподіл.

.

2. Рівномірний розподіл на відрізку .

.

2. Показниковий розподіл.

.

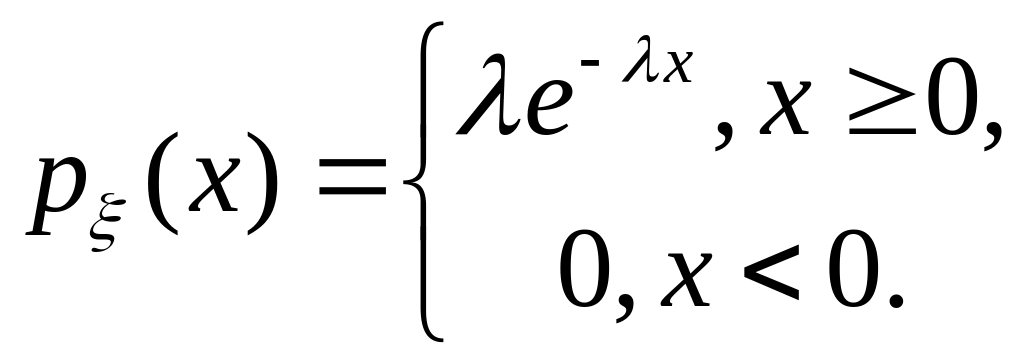
2. Стандартний нормальний розподіл.

За визначенням характеристична функція стандартного нормального розподілу дорівнює

.

Продиференцюємо цю рівність по

.

Таким чином задовольняє диференціальному рівнянню з початковою умовою . Звідси маємо .

4.12. Формули обернення для характеристичних функцій

Кожній випадковій величині відповідає функція розподілу і характеристична функція

.

Функція розподілу за характеристичною функцією відновлюється наступним чином

, (4.19)

де , – будь-які точки неперервності .

Наслідок 4.4. Якщо - абсолютно інтегровна, тобто , то випадкова величина має щільність і

. (4.20)

Нехай – випадковий вектор. Багатовимірною характеристичною функцією випадкового вектору будемо називати

,

де , .

Розглянемо такий приклад. Випадковий вектор має нормальний (або гауссівський) розподіл, якщо його характеристична функція має вид , де - довільний вектор, а - симетрична квадратна матриця розміром невід’ємно визначеної квадратичної форми .

4.13. Неперервна відповідність між функціями розподілу і характеристичними функціями

Будемо говорити, що послідовність функцій розподілу слабко збігається до і писати

,

якщо у кожній точці неперервності граничної функції.

Послідовність випадкових величин , якщо слабко збігається відповідна послідовність функцій розподілу.

Лема 4.12 (Друга теорема Хеллі). Якщо – неперервна, обмежена функція на прямій і , =1, то

. (4.23)

Зауваження. Справедливо і обернене твердження: якщо (4.23) виконується для будь-якої неперервної обмеженої функції, то . Таким чином співвідношення (4.23) можна було б узяти за визначення слабкої збіжності.

Наслідок 4.5. Якщо , то у кожній точці .

Лема 4.13 (Перша теорема Хеллі). З кожної послідовності функцій розподілу можна вибрати слабко збіжну підпослідовність.

Наслідок 4.6. Якщо збігається в кожній точці до деякої функції , неперервної в точці нуль, то - характеристична функція деякого розподілу і .