Понятие графа

Граф — это совокупность непустого множества вершин и множества пар вершин (связей между вершинами).

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Неориентированный граф с шестью вершинами и семью рёбрами

Граф

Граф, или неориентированный граф  — это упорядоченная пара , для которой выполнены следующие условия:

• — это непустое множество вершин, или узлов,

• — это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

(а значит и, ) обычно считаются конечными множествами. Вершины и рёбра графа называются также элементами графа, число вершин в графе  — порядком, число рёбер  — размером графа.

Вершины и называются концевыми вершинами (или просто концами) ребра . Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Ребро называется петлёй, если его концы совпадают, то есть .

Степенью вершины называют количество инцидентных ей рёбер(при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Ориентированный граф

Ориентированный граф (сокращённо орграф)  — это упорядоченная пара , для которой выполнены следующие условия:

• — это непустое множество вершин или узлов,

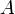• — это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Дуга — это упорядоченная пара вершин , где вершину называют началом, а  — концом дуги. Можно сказать, что дуга ведёт от вершины к вершине .

Смешанный граф

Смешанный граф  — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой , где , и определены так же, как выше.

Ориентированный и неориентированный графы являются частными случаями смешанного.

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

Ориентированным путём в орграфе называют конечную последовательность вершин , для которой все пары являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины и являются концами некоторого ребра, то согласно данному определению, последовательность является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

• Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины.

• Всякий простой неэлементарный путь содержит элементарный цикл.

• Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).

• Петля — элементарный цикл.

Ребро графа называется мостом, если его удаление увеличивает число компонент.

Дополнительные характеристики графов

Граф называется:

• связным, если для любых вершин , есть путь из в .

• сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.

• деревом, если он связный и не содержит простых циклов.

• полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.

• двудольным, если его вершины можно разбить на два непересекающихся подмножества 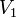и так, что всякое ребро соединяет вершину из с вершиной из .

• k-дольным, если его вершины можно разбить на 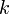непересекающихся подмножества , , …, так, что не будет рёбер, соединяющих вершины одного и того же подмножества.

• полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.

• планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.

• взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.

• Расстоянием между двумя вершинами называется минималь­ная длина из всех возможных маршрутов между этими вершина­ми при условии, что существует хотя бы один такой маршрут. Расстояние обозначается символами  d( A;B)= min|A;B|=k, где  вершины  A и B начало и конец маршрута, k – число, равное наименьшей длине маршрута.

Поскольку рассматриваются конечные графы, минимум мож­но найти всегда. Формально можно ввести расстояние d(VV) = О,  между любой вершиной и ей же самой, что соответствует нулевому маршруту, у которого начало и конец в одной вершине.

В маршруте одно и то же ребро может встретиться несколько раз.

Если ребро встретилось только один раз, то маршрут называ­ется цепью. Запись вида 3-цепь означает, что между двумя точками имеется  цепь – маршрут, длина которого равна 3.

Операции над графами

Над графами, как и над любыми множествами можно выполнять операции объединения и пересечения.

Объединением графов G₁ = (A;B) и G₂ = (C;D) называется граф G= G₁ U G₂, множество вершин которого К= AUC, а мно­жество ребер X=(BUD)

Пересечением графов G₁ = (A;B) и G₂ = (C;D) называется граф G= G₁∩G₂, множество вершин которого К= A∩C, а мно­жество ребер X=(B∩D).

Подграфом данного графа называется граф все вершины  и ребра которого являются подмно­жествами множества вершин и ребер этого графа.

Обозначения подграфа, его вершин  и ребер можно  так, как это принято для обозначения подмножеств или ввести другие буквы. А именно, если граф A=(N;M) есть подграф графа G=(V, X), то A ÌG, причем NÌV и MÌX

Кольцевой суммой G₁ = (A;B) и G₂ = (C;D) называется граф G= G₁ U G₂, множество вершин которого К= AUC, а мно­жество ребер X=(BUD)\ (B∩D).

2.3. Деревья. Лес. Бинарные деревья

Деревом называют конечный связный граф с выделенной вер­шиной (корнем), не имеющий циклов Вершины графа – дерева, называются узлами.

Для каждой пары вершин дерева – узлов - существует един­ственный маршрут, поэтому вершины удобно классифицировать по степени удаленности от корневой вершины. Расстояние до кор­невой вершины К₀ называется ярусом s вершины, s= d(V₀ V).

Поскольку маршрут между двумя вершинами единственный, то, применяя это свойство к смежным вершинам, можно заклю­чить, что любая ветвь является мостом. Действительно, при уда­лении ребра этот единственный маршрут прерывается. Тогда граф распадается на два подграфа. В одном из них остается корневая вершина, и этот граф  тоже будет являться деревом. В другом графе выделяется  вершина, инцидентная удаленному мосту. Второй подграф также будет являться деревом.

Каждая висячая вершина дерева называется его листом.

Каждая не висячая вершина дерева, содержит не менее двух ребер, которые часто  называются  поддеревьями.

Теорема 7. Граф является деревом тогда и только тогда, когда выполняется хотя бы одно из условий:

граф G(V, X) связен и не содержит циклов;

граф G(V, X) не содержит циклов и имеет п-1 ребро;

граф G(V, X) связен и имеет п-1 ребро;

граф G(V, X) не содержит циклов, но добавление ребра между несмежными вершинами приводит к появлению одного и только од­ного элементарного цикла;

граф G( У, X) связный, но утрачивает это свойство после удале­ния любого ребра;

в графе G(V, X) всякая пара вершин соединена цепью, и только одной.

Дерево с п вершинами имеет п-1 ребро, поэтому оно будет минимальным связным графом.

Висячие вершины, за исключением корневой, называются листьями.

Лесом называется граф, полученный в результате упорядоченного объединения не пересекающихся деревьев. Так, если   графы  A,S.D.F – деревья, то  граф G= A∪S∪D∪F есть лес

Компонентами связности леса являются деревья. Остовом связно­го графа G называется любой его подграф F, содержащий все вер­шины графа G и являющийся деревом (говорят: покрывающим его деревом»).

Если граф F есть остов леса G, то дополнения F’ до G является кодеревом.

Дерево может быть представлено расслоенным на ярусы (уров­ни), при этом ветвям, попавшим в один ярус, соответствует оди­наковая длина пути исходного графа. Число путей в каждом дере­ве соответствует числу висячих вершин (листьев).

При описании деревьев принято использовать термины: отец, сын, предок, потомок.

Каждая вершина дерева называется узлом, причем каждый узел является корнем дерева, имеющего свои поддеревья Количество их не превышает числа всех узлов дерева..

Очевидно, что узел без поддеревьев называется листом и является висячей вер­шиной.

Узел k-го яруса называется отцом узла (k+ 1)-го яруса, если они смежные.

Узел (k+ 1)-го яруса называется сыном узла k-ro яруса.

Два узла, имеющие одного отца, называются братьями.

Вполне очевидно, что отца можно назвать предком, а сыновей – потомками.

Упорядоченным деревом называется дерево, в котором поддере­вья каждого узла образуют упоря­доченное подмножество.

Для упоря­доченных деревьев принята терми­нология: старший и младший сын для обозначения соответственно первого и последнего сыновей не­которого узла.

Дерево, когда каждый узел которого является либо листом, либо образует два поддерева: левое и правое. называется бинарны­ми деревьями и используется при делении множества на два взаимоисключающих подмножества по какому-то признаку (так называ­емое дихотомическое деление).

Например для бинарного дерева можно указать, что  отец A, сыновья В и С, при­чем В – левый, а С – правый потомки ( по алфавиту и запись слева направо по строчке (ярусу дерева)

Строго бинарным деревом называется такой граф, у которого каждый узел, не являющийся листом, содержит два и только два поддерева – ле­вое и правое.

Бинарное дерево уровня п называется полным, если каждый его узел уровня п является листом, а каждый узел уровня мень­ше, чем n, имеет непустое левое и правое поддеревья.

Бинарные деревья применяются в информатике для поиска од­ного из двух возможных вариантов ответа. Например, при поиске данных, когда необходимо сравнить каждый элемент списка с об­разцом, и если значения совпадают, то процесс поиска завершен, а если не совпадают, то поиск данных продолжается. Впервые по­нятие двоичного дерева ввел в III в. римский философ Порфирий.

Примером бинарных деревьев может служить турнирная таблица спортивных игр, например волейбол, шахматы и др.Что бы быть победителем, надо выиграть в финале, где встречаются две команды, которые победили в полуфинале, а перед этим  победили  в четверть финале и т.д. К таким относится также олимпийская система соревнований

Цикломатическим числом графа называется число v = m + c – n, где:

m – количество ребер;

c - количество связных компонент графа;

п – количество вершин.

Цикломатическое число дерева равно нулю. Цикломатическое число леса равно сумме цикломатических чисел составных связных компонент – деревьев и, следовательно, тоже равно нулю. Для остальных гра­фов цикломатические числа – положительные.

Например, для полного графа, имеющего пять вершин и 10 ребер цикломатическое число равно v = 10 + 1 – 5 = 6.

4. Способы задания графа. Изоморфные графы

Графы могут задаваться следующими способами:

1. Геометрическим способом – рисунки, схемы, диаграммы,

2. Алгебраическим способом – перечислением вершин и ребер,

3. Табличным способом.

4. Матричным способом.

Человеку удобно работать с графом-рисунком, так как он может легко установить связь между вершинами в на­глядном виде с помощью ребер, изображаемых непрерывными линиями. Такое геометрическое представление плоского графа на­зывается его реализацией.

Для машинной обработки удобнее за­дать граф в алгебраической форме – перечислением (списком) вершин или ребер.

При переходе от алгебраического способа к геометриче­скому одному и тому же графу могут соответствовать различные изображения – изоморфные графы, при этом от правильного изоб­ражения зависит, например, свойство плоской реализуемости. Для этого нужно правильно задать сам граф.

Основным способом задания графа является перечисление всех его вершин и ребер. Но такое представление, во-первых, несим­метрично (с ним трудно работать, особенно ЭВМ), во-вторых, для указания каждого ребра нужно еще раз выписывать соответ­ствующие вершины, что плохо с точки зрения сжатия и хранения информации.

При задании графа таблицей составляется таблица, состоящей из п строк (вершины) и т столбцов (ребра). На пересечении строк и столбцов пишутся соответствующие знаки, которые показывают отношение  (инцидентность) вершины и ребра. Это может быть знаки “+” и “-”, числа 0,1,-1 и др.

Главным во всех способах задания графа (диаграммой, матрицей, таблицей) является указание соответствия между множествами п вершин V_t к т ребер X-_t.

Пусть дан граф G(V, X), где V= {V₁, V₂ …V_n} – вершины, а Х= {Х₁, Х₂ .,., Х_m} – ребра, среди которых могут и кратные  ребра (есть  вершины, которые  соединяет несколько ребер).

Матрицей инцидентности данного графа будет таблица, состоящая из n строк (вершины) и т столбцов (ребра).

При рассмотрении неориентированного графа на пересечении строк и столбцов ставится число 1, если соответствующие вершина и ребро  инцидентны и ставится число 0,  они не инцидентны.

При рассмотрении ориентированного графа на пересечении строк и столбцов ставится число 1, если из  вершины выходит  соответствующее ее ребро.  Если в вершину входит ребро, то ставят число -1. Если вершина не инцидентна ребру и, то ставится число 0

Очевидно, что в каждом столбце матрицы инцидентности долж­но быть только два ненулевых числа, так как ребро инцидентно двум вершинам. Число ненулевых элементов каждой строки – сте­пень соответствующей вершины.

Матрицы инцидентности прямоугольные, если число строк и столбцов различно. Если число вершин и ребер в графе одинаковое, то получается квадратная матрица.

Матрицу можно сделать квадратной для любого графа без кратных ребер. В таких случаях строки  и столбцы  изображают вершины. На пересечении строк и столбцов ставится число 1, если соответствующие вершины соединены ребром и ставится число 0, если вершины не соединены.

Для неориентированного графа ребра одновременно принадлежат или не принадлежат графу, так как символизируют одно и то же ребро. Матрица смеж­ности неориентированного графа является симметрической и не меняется при транспонировании.

Хотя формально каждая вершина всегда смежная сама с собой, в матрице смежности мы будем ставить 0, если у нее нет петли, и 1, если есть одна петля.

Если граф имеет матрицу смежности и не имеет петель, на главной диагонали у него всегда стоят нули.

Задание Составить таблицу и матрицу  инцидентности  для орграфа, изображенного на рисунке, который имеет 3вершины и  4 ребра.

Ответ.