
- •Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «кемеровский государственный университет»
- •Кафедра автоматизации исследований
- •И технической кибернетики
- •Дискретная математика
- •Содержание
- •Глава 1. Теория множеств. Дискретная теория вероятности......5
- •Глава 2. Теория графов.....................................................................53
- •Глава 3. Дискретные структуры: конечные автоматы, коды...76
- •Глава 4. Алгебра логических функций..........................................88
- •Глава 5. Логика высказываний и логика предикатов..............109
- •Глава 6. Схемы переключателей. Комбинационные схемы...................................................................................................123
- •Глава 1. Теория множеств. Дискретная теория вероятности
- •Множества и операции над ними
- •Упражнения
- •1.2. Векторы и прямые произведения множеств. Проекция вектора на ось
- •Упражнения
- •1.3. Комбинаторика Правило суммы
- •Правило произведения
- •Число размещений без повторений
- •Число размещений с повторениями
- •Число перестановок без повторений
- •Число сочетаний без повторений
- •Упражнения
- •1.4. Введение в дискретную теорию вероятностей
- •Свойства элементарных событий:
- •Соотношения между событиями:
- •Свойства операций над событиями:
- •Упражнения
- •1.5. Соответствия и функции
- •Взаимно однозначные соответствия и мощность множеств
- •Упражнения
- •1.6. Отношения
- •Способы задания бинарных отношений
- •Свойства бинарных отношений
- •Отношение эквивалентности
- •Отношение порядка
- •Лексико-графический порядок.
- •Упражнения
- •1.7. Операции и алгебры
- •Свойства бинарных алгебраических операций
- •1.8. Гомоморфизм и изоморфизм алгебр
- •Полугруппы, группы, решетки
- •Упражнения
- •Глава 2. Теория графов
- •2.1. Основные определения, способы задания, основные классы, изоморфизм графов
- •Способы задания графа
- •Степени вершин графа
- •Части, суграфы и подграфы
- •Операции над частями графа
- •Графы и бинарные отношения
- •Упражнения
- •Среди пар графов, изображенных на рисунке, указать пары изоморфных графов и пары неизоморфных графов. Ответ обосновать.
- •Маршруты, цепи и циклы. Расстояния, диаметры, центры. Обходы. Разделяющие множества и разрезы
- •Упражнения
- •Деревья, их свойства. Характеристические числа графов. Сети
- •Упражнения
- •Глава 3. Дискретные структуры: конечные автоматы, коды
- •3.1. Машина Тьюринга
- •Упражнения
- •Основы теории кодирования
- •Упражнения
- •Глава 4. Алгебра логических функций
- •4.1. Основные определения
- •Упражнения
- •4.2. Эквивалентные преобразования
- •Упражнения
- •4.3. Дизъюнктивные и конъюнктивные нормальные формы
- •Упражнения
- •4.4. Дизъюнктивные нормальные формы и импликанты
- •Упражнения
- •4.5. Минимизация днф. Тупикова днф
- •Упражнения
- •4.6. Алгебра Жегалкина
- •Упражнения
- •4.7. Двойственность в алгебре логики. Самодвойственные функции
- •Принцип двойственности
- •Упражнения
- •4.8. Функциональная полнота систем
- •Упражнения
- •Глава 5. Логика высказываний и логика предикатов
- •5.1. Логика высказываний
- •Алгебра логики
- •Исчисление высказываний
- •Упражнения
- •5.2. Логика предикатов
- •Упражнения
- •Глава 6. Схемы переключателей. Комбинационные схемы
- •Схемы переключателей
- •Комбинационные схемы
- •Упражнения
- •Литература
- •650043, Кемерово, ул. Красная, 6.
5.2. Логика предикатов
С помощью формул логики высказываний можно описать структуру сложных высказываний. Для описания внутренней логической структуры простых высказываний (т.е. высказываний, не содержащих связок) используются другие средства, которые вместе с логикой высказываний образуют логику предикатов.
Чтобы яснее представить о какой логической структуре идет речь, рассмотрим пять высказываний:
15 – нечетное число.
8 – нечетное число.
6
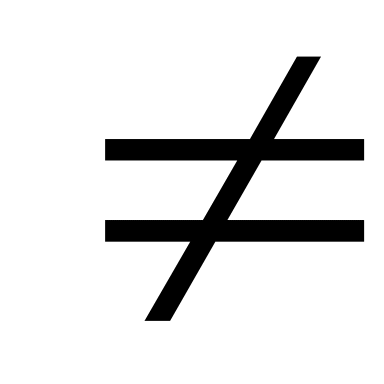 5.
5.В Ярославле жителей больше, чем в Вязьме.
В Москве жителей больше, чем в любом другом городе России.
Все эти высказывания – простые и, следовательно, в логике высказываний изображаются одной буквой. Все, что о них можно сказать в этой логике, – это то, что высказывание (2) ложно, а остальные – истинны.
В то же время ясно, что между высказываниями (1) и (2) или между (4) и (5) сходства гораздо больше, чем между (1) и (5).
В высказываниях (1) и (2) речь идет о числах, которым приписывается одно и то же свойство – нечетность. В высказывании (3) утверждается наличие отношения неравенства между числами. В высказываниях (4) и (5) говорится о городах, относительно которых утверждается наличие некоторого отношения между ними – «иметь больше жителей».
Числа и города –
это объекты.
Множество объектов (целых чисел, городов
России и т.д.), о которых делаются
утверждения, называется предметной
областью,
а сами утверждения об отношениях между
![]() объектами называются nместными
предикатами.
объектами называются nместными
предикатами.
С математической точки зрения:
nместный
предикат
– это функция
![]() от
переменных, причем переменные принимают
значения из предметной области, а функция
от
переменных, причем переменные принимают
значения из предметной области, а функция
![]() принимает два логических значения –
истинно и
ложно.
принимает два логических значения –
истинно и
ложно.
Нечетность – это
одноместный предикат. Если его обозначить
через
![]() ,
тогда высказывания (1) и (2) запишутся
как
,
тогда высказывания (1) и (2) запишутся
как
![]() и
и
![]() ,
т.е. как один и тот же предикат нечетности
с разными значениями (15 и 8) переменной
,
взятыми из одной и той же предметной
области целых чисел.
,
т.е. как один и тот же предикат нечетности
с разными значениями (15 и 8) переменной
,
взятыми из одной и той же предметной
области целых чисел.
«Иметь больше
жителей» – это двуместный предикат
![]() .
Высказывание (4) можно записать как
.
Высказывание (4) можно записать как
![]() .
.
Неравенство –
тоже двуместный предикат, для обозначения
которого можно сохранить обычную запись:
![]() .
.
Таким образом,
формулы вида
и
это переменные высказывания, которые
становятся истинными или ложными при
подстановке вместо
и
![]() предметных констант – конкретных
объектов из предметных областей.
предметных констант – конкретных
объектов из предметных областей.
Кроме того, из предикатов можно получать конкретные высказывания, не содержащие предметных констант, а утверждающих нечто обо всей предметной области.
В естественном языке это делается с помощью оборотов «для всех (т.е. для всех объектов) справедливо, что…» и «существует такой , что…».
В языке формул
логики предикатов этим оборотам
соответствуют специальные знаки –
кванторы:
квантор
общности
![]() и квантор
существования
и квантор
существования
![]() .
.
Присоединение квантора с переменной к предикатной формуле, содержащей , называется навешиванием квантора на переменную . Переменная при этом называется связанной, вместо нее подставлять предметные константы уже нельзя.
Например, формула означает «для всех целых чисел справедливо то, что они нечетны» или, короче, «все целые числа – нечетны». Это – конкретное высказывание, которое ложно. Формула означает истинное высказывание «существуют нечетные целые числа».
Если квантор
навешивается на формулу с несколькими
предметными переменными, то он уменьшает
число свободных (несвязанных) переменных
в этой формуле. Например, формула
![]() обозначает высказывание «в
городе
больше
жителей, чем в любом городе
«
и содержит одну свободную переменную
.
Это высказывание ложно для любого
,
потому что «любой
город»
подразумевает в том числе и
,
но ни в каком городе не может быть больше
жителей, чем в нем самом. «Шансы на
истинность» имеет уточненное высказывание:
«в городе
больше
жителей, чем в любом другом городе
,
не совпадающем с
»:
обозначает высказывание «в
городе
больше
жителей, чем в любом городе
«
и содержит одну свободную переменную
.
Это высказывание ложно для любого
,
потому что «любой
город»
подразумевает в том числе и
,
но ни в каком городе не может быть больше
жителей, чем в нем самом. «Шансы на
истинность» имеет уточненное высказывание:
«в городе
больше
жителей, чем в любом другом городе
,
не совпадающем с
»:
![]() ,
,
в которой оба вхождения переменной связаны квантором (с помощью скобок). Подстановка «Москва» вместо дает формулу, выражающую истинное высказывание (5).
Как и в логике высказываний, в логике предикатов имеются эквивалентные соотношения, позволяющие преобразовывать предикатные формулы. Например,
один квантор можно выразить через другой:
![]() ,
,
![]() ,
,
формулу, не содержащую переменную , можно вынести за пределы действия квантора, связывающего :
![]() ;
;
![]() .
.
Однако, в целом, логику предикатов не удается представить в виде алгебры, столь же эффективной как алгебра логики (т.к. вычисление истинности предикатов, содержащих кванторы, в общем случае заключается в подстановке всех возможных значений предметных переменных, которых может быть бесконечное множество).
Поэтому логика предикатов организуется в виде исчисления предикатов, которое содержит аксиомы и правила вывода исчисления высказываний, а также дополнительные предикатные аксиомы и правила вывода.
В качестве аксиом обычно принимаются две формулы:
![]() ,
(1)
,
(1)
![]() ,
(2)
,
(2)
где
![]() – любая предикатная формула, содержащая
свободную переменную
,
а в качестве правил
вывода –
правила, вводящие кванторы:
– любая предикатная формула, содержащая
свободную переменную
,
а в качестве правил
вывода –
правила, вводящие кванторы:
![]() ,
(3)
,
(3)
![]() ,
(4)
,
(4)
в
этих правилах требуется, чтобы формула
![]() содержала свободную переменную
,
а
содержала свободную переменную
,
а
![]() ее не содержала.
ее не содержала.
Пример 1.
Рассмотрим известнейший силлогизм, на протяжении двух тысячелетий переходящий из одних ученых трудов в другие:
Все люди смертны.
Сократ – человек. .
Следовательно, Сократ – смертен.
Этот силлогизм является частным случаем «первой фигуры» силлогизма:
Все, кто обладает свойством P, обладает свойством Q.
y обладает свойством P. .
Следовательно, y обладает свойством Q.
Обосновать силлогизм на языке предикатов – это значит записать три его утверждения на этом языке и показать, что в исчислении предикатов из первых двух утверждений (посылок) выводимо третье (заключение).
Предикатная запись первой фигуры силлогизма выглядит так:
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Формальный вывод заключения (7) из посылок (5) и (6) состоит в следующем:
1. В первую предикатную
аксиому (1) вместо
![]() подставим
подставим
![]() (импликация:
если …,
то …). Получим:
(импликация:
если …,
то …). Получим:
![]() .
(8)
.
(8)
2. Из формул (8) и (5) по правилу Modus Ponens ( ) следует, что выводима формула
![]() .
(9)
.
(9)
3. Из формул (9) и
(6) по правилу Modus
Ponens выводима формула
![]() ,
что и требовалось:
,
что и требовалось:
![]() .
.
Префиксной нормальной формой называется выражение вида:
![]() ,
,
где
![]() кванторы,
навешанные на переменные
кванторы,
навешанные на переменные
![]()
![]() – предикатная формула, имеющая вид ДНФ.
– предикатная формула, имеющая вид ДНФ.
