
- •Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «кемеровский государственный университет»
- •Кафедра автоматизации исследований
- •И технической кибернетики
- •Дискретная математика
- •Содержание
- •Глава 1. Теория множеств. Дискретная теория вероятности......5
- •Глава 2. Теория графов.....................................................................53
- •Глава 3. Дискретные структуры: конечные автоматы, коды...76
- •Глава 4. Алгебра логических функций..........................................88
- •Глава 5. Логика высказываний и логика предикатов..............109
- •Глава 6. Схемы переключателей. Комбинационные схемы...................................................................................................123
- •Глава 1. Теория множеств. Дискретная теория вероятности
- •Множества и операции над ними
- •Упражнения
- •1.2. Векторы и прямые произведения множеств. Проекция вектора на ось
- •Упражнения
- •1.3. Комбинаторика Правило суммы
- •Правило произведения
- •Число размещений без повторений
- •Число размещений с повторениями
- •Число перестановок без повторений
- •Число сочетаний без повторений
- •Упражнения
- •1.4. Введение в дискретную теорию вероятностей
- •Свойства элементарных событий:
- •Соотношения между событиями:
- •Свойства операций над событиями:
- •Упражнения
- •1.5. Соответствия и функции
- •Взаимно однозначные соответствия и мощность множеств
- •Упражнения
- •1.6. Отношения
- •Способы задания бинарных отношений
- •Свойства бинарных отношений
- •Отношение эквивалентности
- •Отношение порядка
- •Лексико-графический порядок.
- •Упражнения
- •1.7. Операции и алгебры
- •Свойства бинарных алгебраических операций
- •1.8. Гомоморфизм и изоморфизм алгебр
- •Полугруппы, группы, решетки
- •Упражнения
- •Глава 2. Теория графов
- •2.1. Основные определения, способы задания, основные классы, изоморфизм графов
- •Способы задания графа
- •Степени вершин графа
- •Части, суграфы и подграфы
- •Операции над частями графа
- •Графы и бинарные отношения
- •Упражнения
- •Среди пар графов, изображенных на рисунке, указать пары изоморфных графов и пары неизоморфных графов. Ответ обосновать.
- •Маршруты, цепи и циклы. Расстояния, диаметры, центры. Обходы. Разделяющие множества и разрезы
- •Упражнения
- •Деревья, их свойства. Характеристические числа графов. Сети
- •Упражнения
- •Глава 3. Дискретные структуры: конечные автоматы, коды
- •3.1. Машина Тьюринга
- •Упражнения
- •Основы теории кодирования
- •Упражнения
- •Глава 4. Алгебра логических функций
- •4.1. Основные определения
- •Упражнения
- •4.2. Эквивалентные преобразования
- •Упражнения
- •4.3. Дизъюнктивные и конъюнктивные нормальные формы
- •Упражнения
- •4.4. Дизъюнктивные нормальные формы и импликанты
- •Упражнения
- •4.5. Минимизация днф. Тупикова днф
- •Упражнения
- •4.6. Алгебра Жегалкина
- •Упражнения
- •4.7. Двойственность в алгебре логики. Самодвойственные функции
- •Принцип двойственности
- •Упражнения
- •4.8. Функциональная полнота систем
- •Упражнения
- •Глава 5. Логика высказываний и логика предикатов
- •5.1. Логика высказываний
- •Алгебра логики
- •Исчисление высказываний
- •Упражнения
- •5.2. Логика предикатов
- •Упражнения
- •Глава 6. Схемы переключателей. Комбинационные схемы
- •Схемы переключателей
- •Комбинационные схемы
- •Упражнения
- •Литература
- •650043, Кемерово, ул. Красная, 6.
Упражнения
Укажите смысловые связки естественного языка, соответствующие основным операциям над множествами: дополнение (– НЕ), объединение (сумма) (– ИЛИ), пересечение (произведение) (– И), разность (– БЕЗ).
Пусть
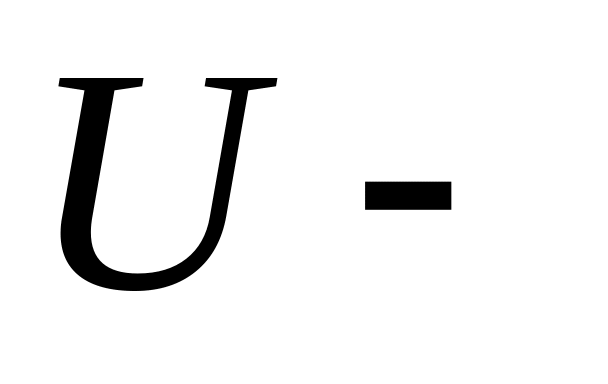 множество
сотрудников некоторого предприятия;
множество
сотрудников некоторого предприятия;
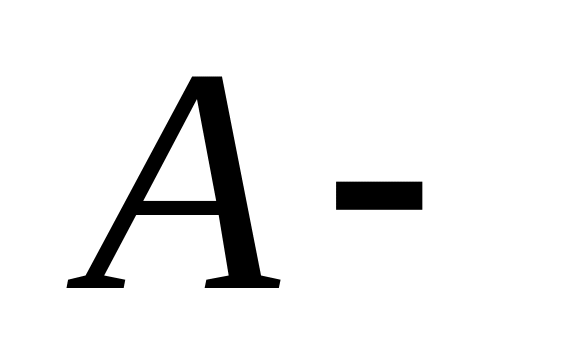 множество
всех сотрудников старше 40 лет;
множество
всех сотрудников старше 40 лет;
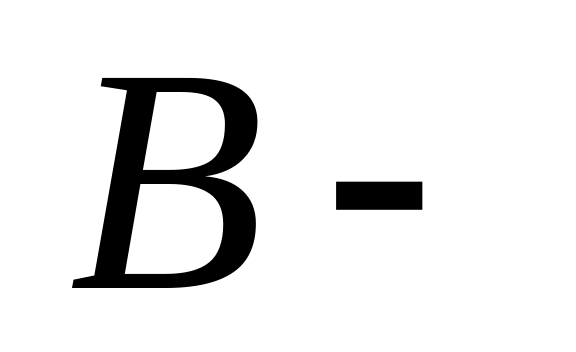 множество
сотрудников, имеющих стаж более 10 лет;
множество
сотрудников, имеющих стаж более 10 лет;
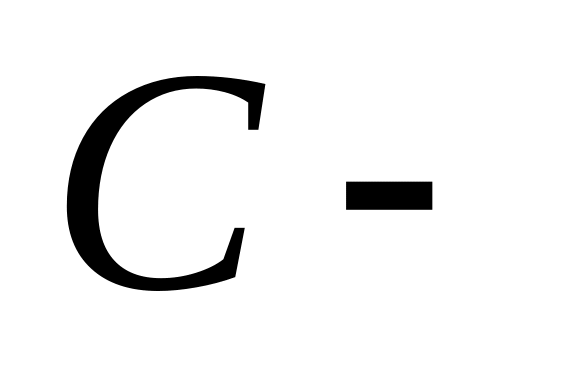 множество
служащих;
множество
служащих;
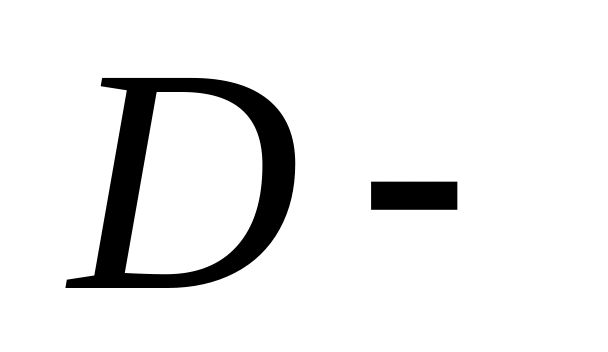 множество
рабочих. Каков содержательный смысл
каждого из нижеследующих множеств?
Изобразить графически (с помощью
диаграмм Эйлера – Венна) эти множества.
множество
рабочих. Каков содержательный смысл
каждого из нижеследующих множеств?
Изобразить графически (с помощью
диаграмм Эйлера – Венна) эти множества.
1)
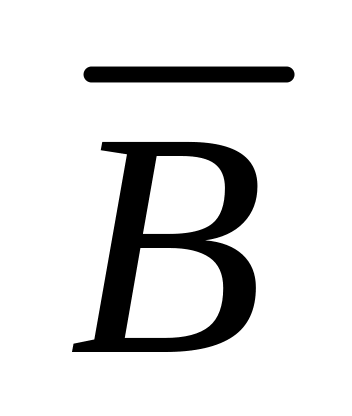 ;
;5)
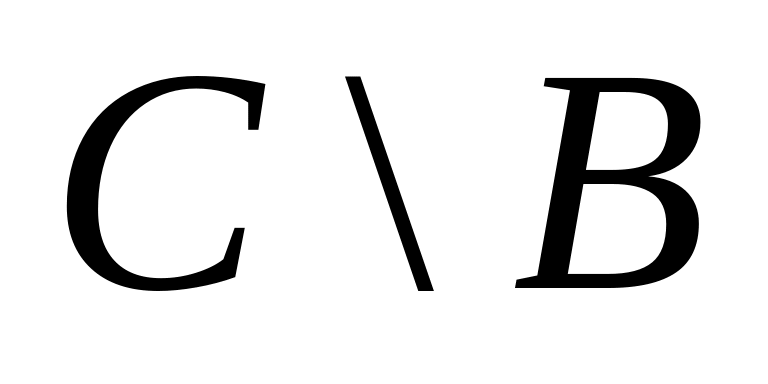 ;
;9)
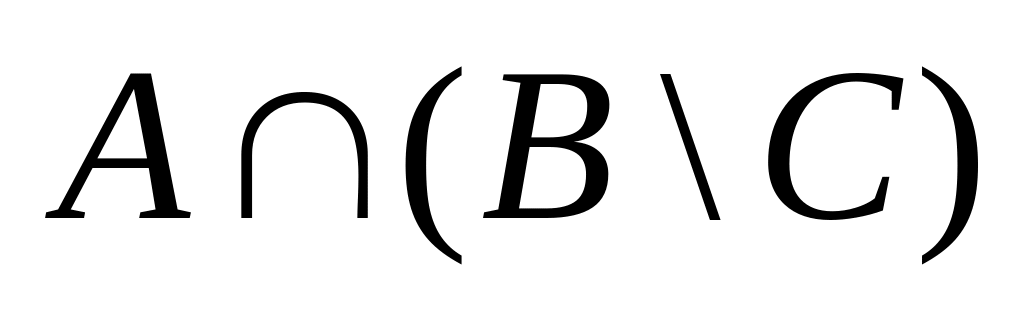 ;
;2)
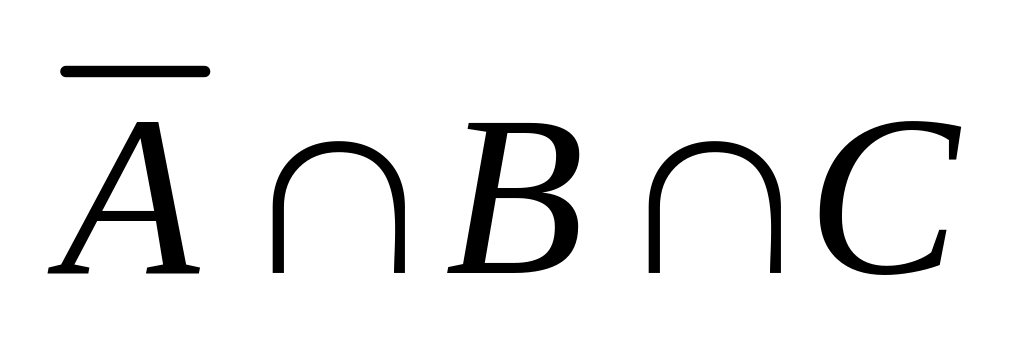 ;
;6)
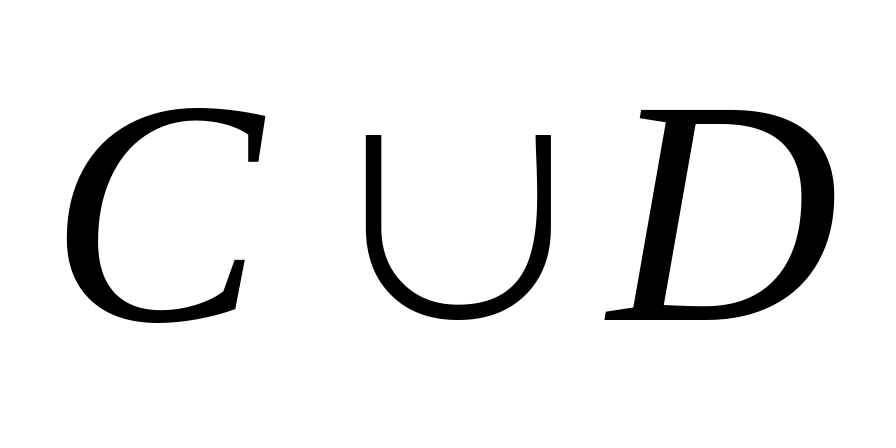 ;
;10)
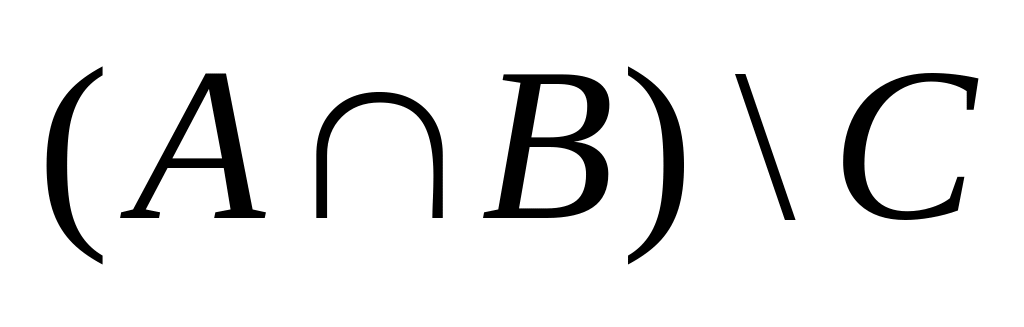 ;
;3)
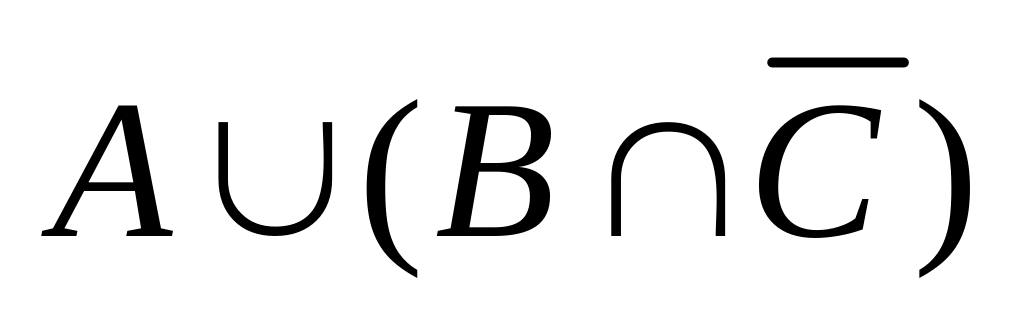 ;
;7)
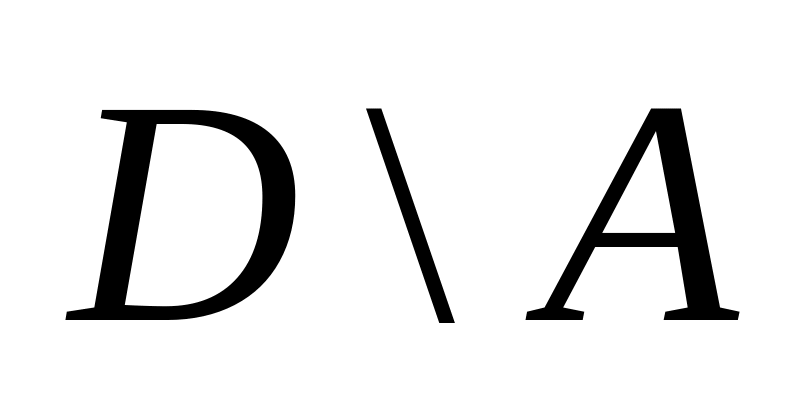 ;
;11)
 ;
;4)
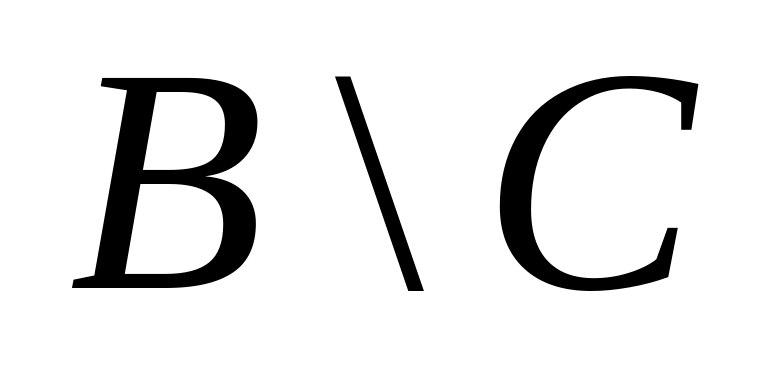 ;
;8)
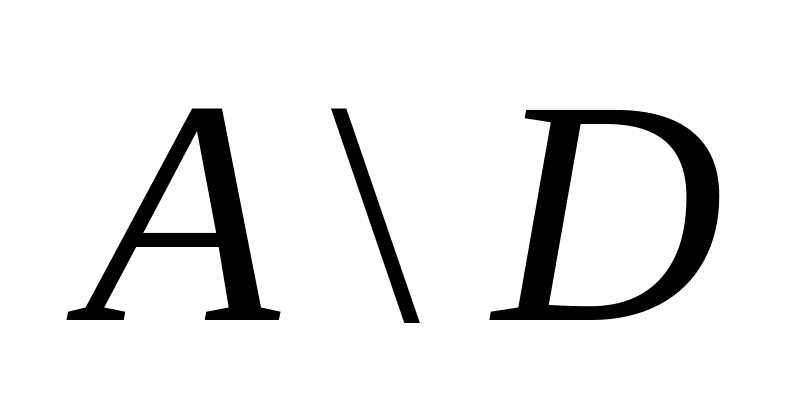 ;
;12)
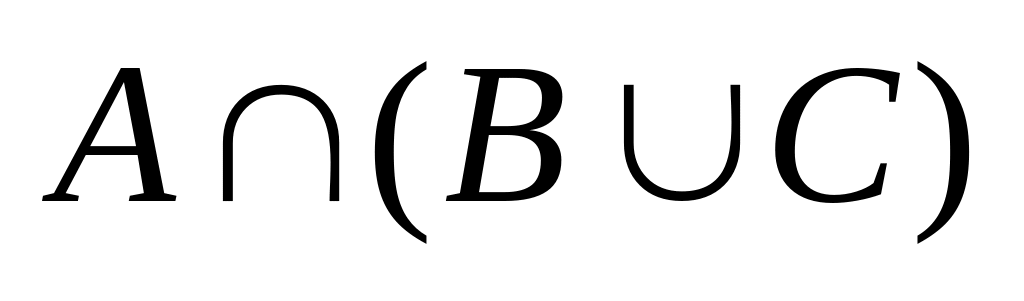 .
.Заданы множества А = {1, 5, 7, 9, 12} , B = {5, 7, 9, 11, 13} и С = {1, 2, 3, 8, 10}, являющиеся подмножеством универсального множества U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Найти следующие множества и их мощности:
1)
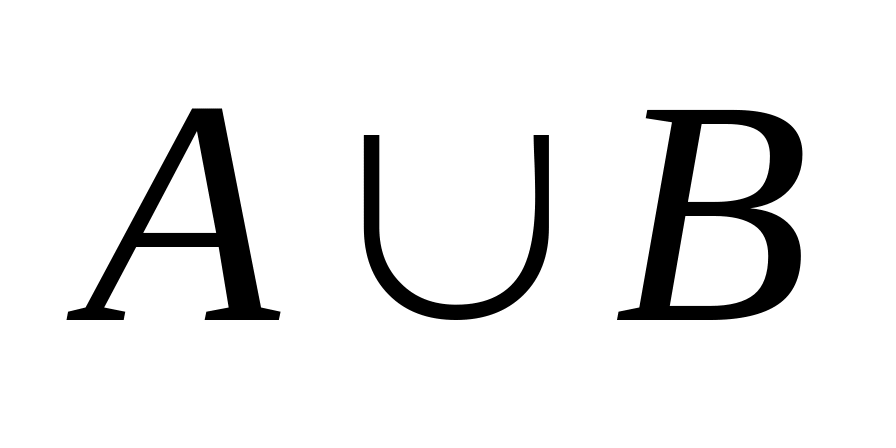 ;
;5)
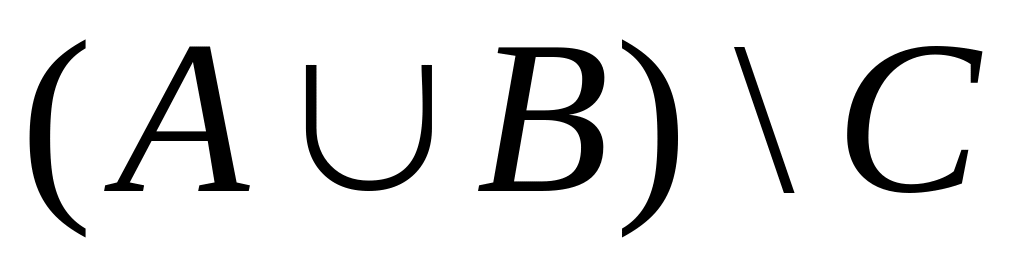 ;
;2) ;
6) ;
3) ;
7)
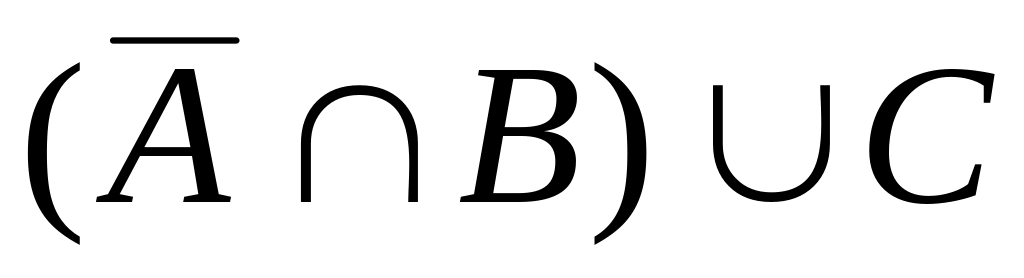 ;
;4) ;
8)
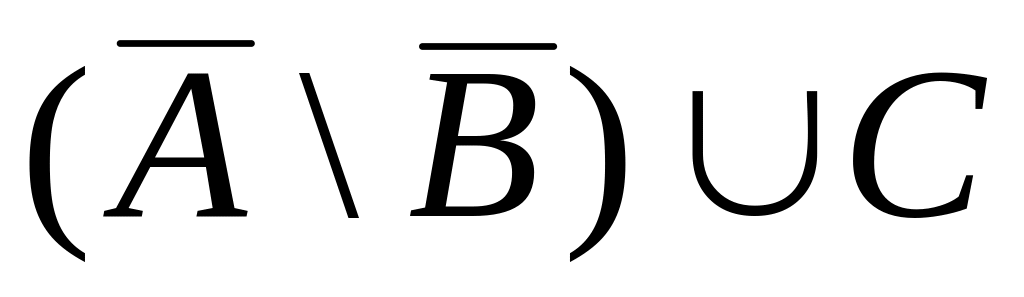 .
.По заданным промежуткам А и B на числовой оси определить
 ;
;
;
;
.
;
;
;
;
.
1)
![]() и
и
![]() ;
3)
;
3)
![]() и
и
![]() ;
;
2)
![]() и
и
![]() ; 4)
; 4)
![]() и
и
![]()
Задана система множеств
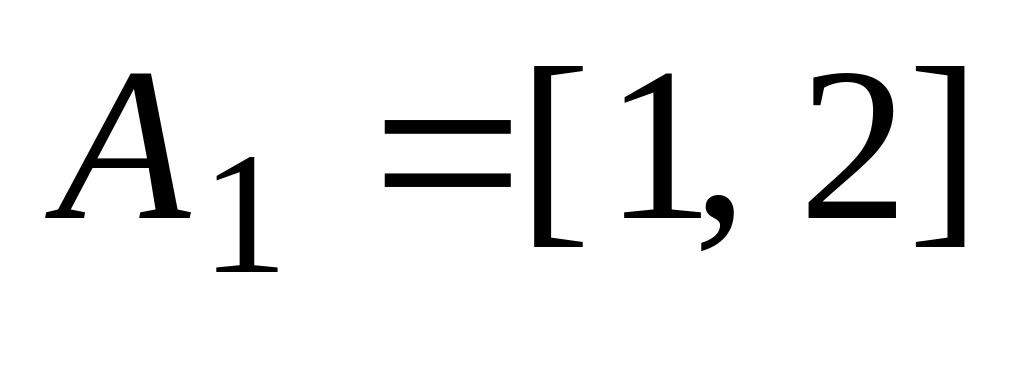 ,
,
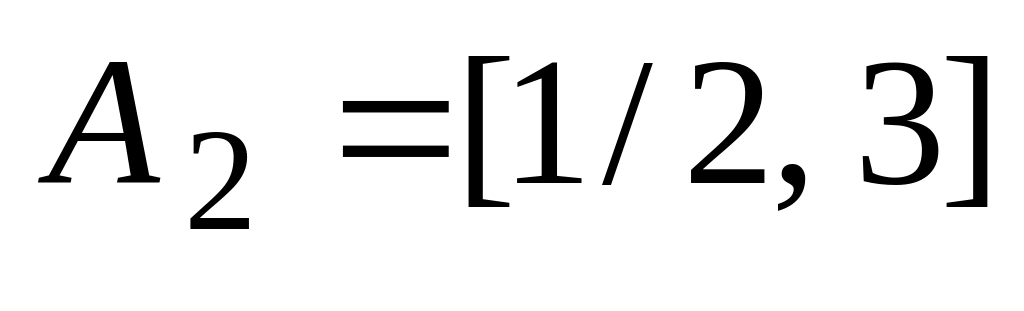 ,
,
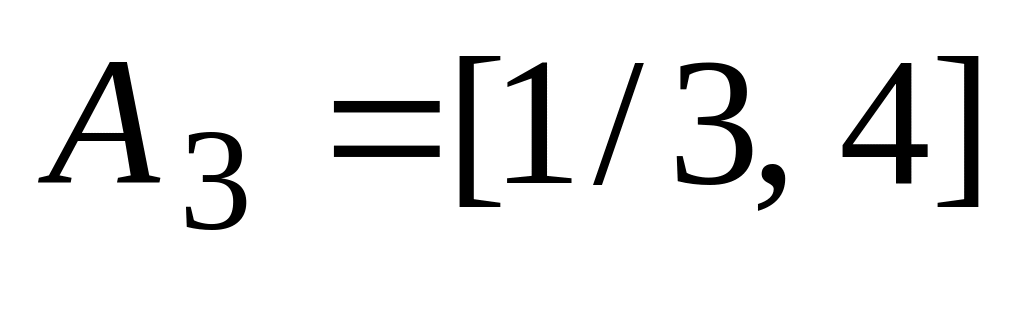 ,
…,
,
…,
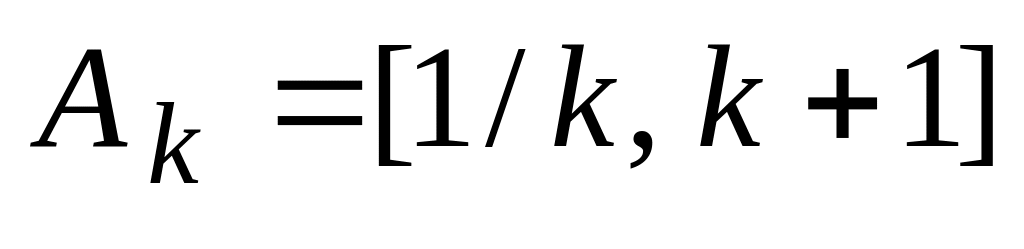 .
Найти
.
Найти
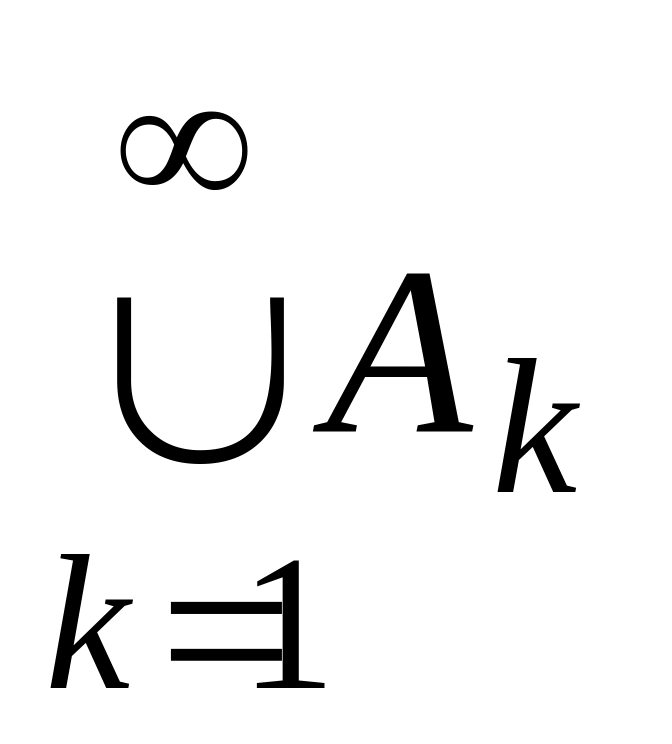 и
и
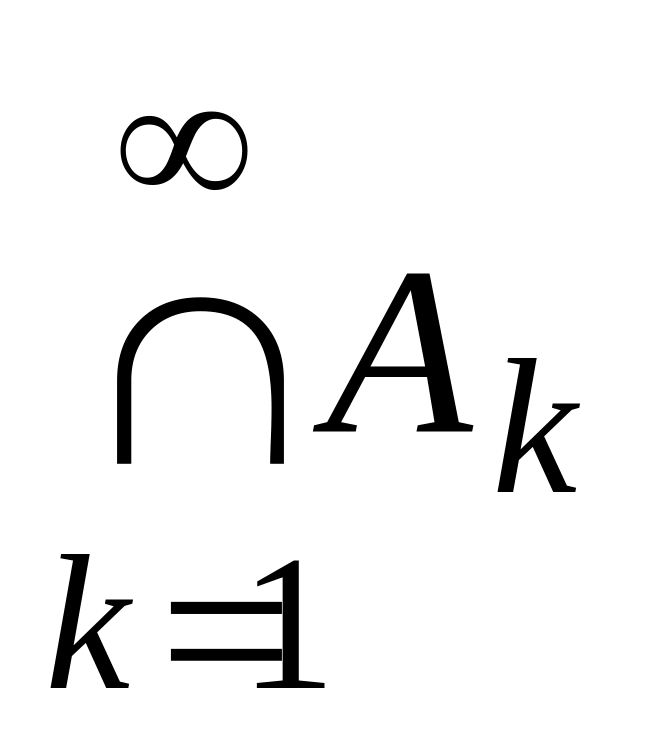 .
.
Задана система множеств
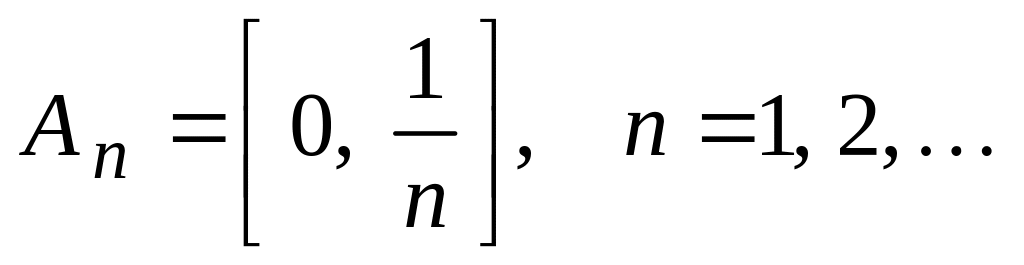 .
.
Найти
![]() и
и
![]() .
.
Пусть А и В – произвольные подмножества универсального множества I. Доказать графически, что:
1)
![]() ; 4)
; 4)
![]() ;
;
2)
![]() ; 5)
; 5)
![]() ;
;
3)
![]() ;
6)
;
6)
![]() .
.
Доказать (аналитически), что
 .
.
Указание: воспользоваться тождеством
![]() .
.
Существуют ли такие множества А, В и С, что
 ,
,
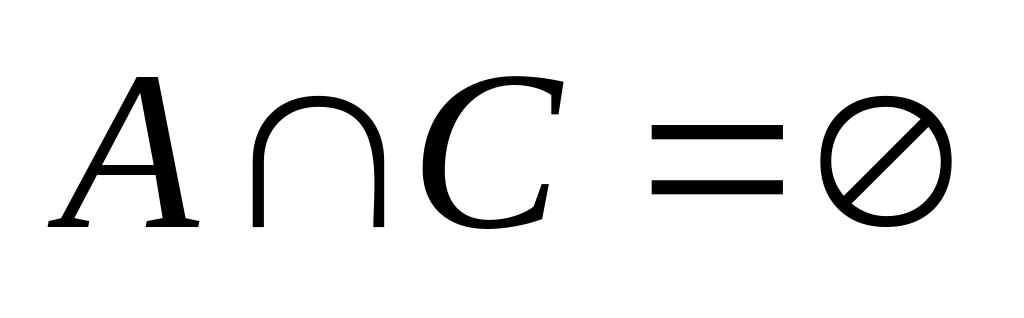 и
и
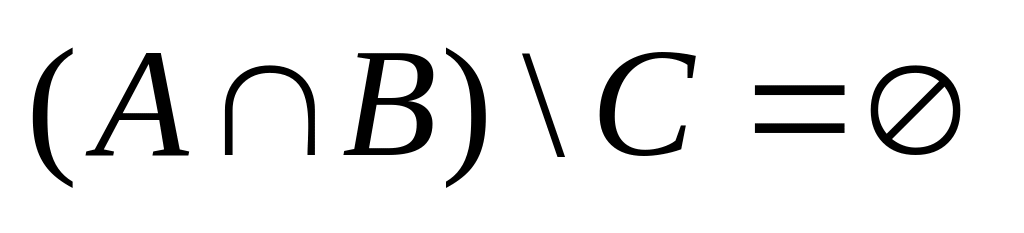 ?
?
Указание: построить диаграмму Эйлера – Венна.
11. Построить из
множества А,
В и С
результат операций над ними.
![]() {1,
2, 3},
{1,
2, 3},
![]() {1,
3, 5},
{1,
3, 5},
![]() {2,
3, 4, 6}.
{2,
3, 4, 6}.
1)
![]() ;
2)
;
2)
![]() .
.
12. Пусть Множества А, В, С пересекаются в наиболее общем случае. Изобразить на диаграмме Эйлера Результат следующих действий:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
Пусть
 и
и
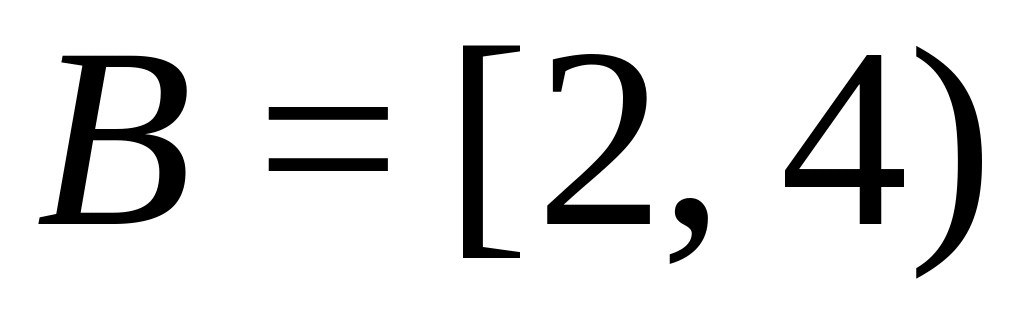
промежутки на числовой оси. Найти
промежутки на числовой оси. Найти
 ;
;
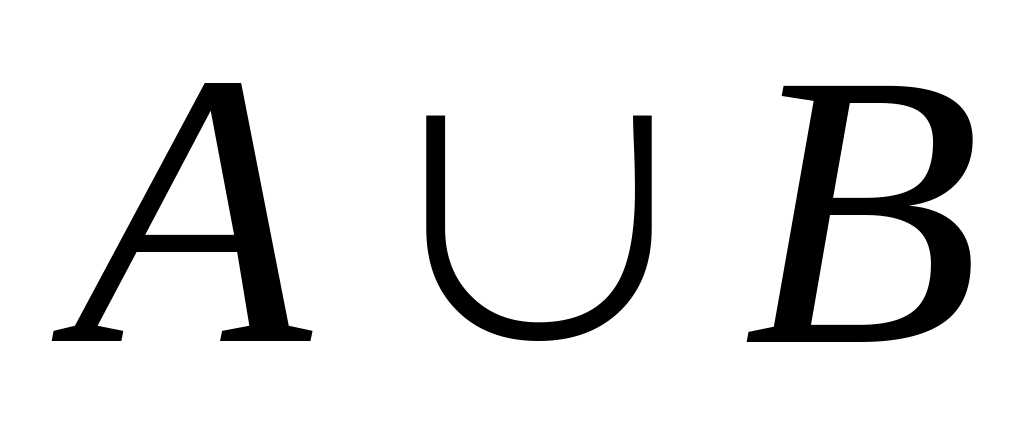 ;
;
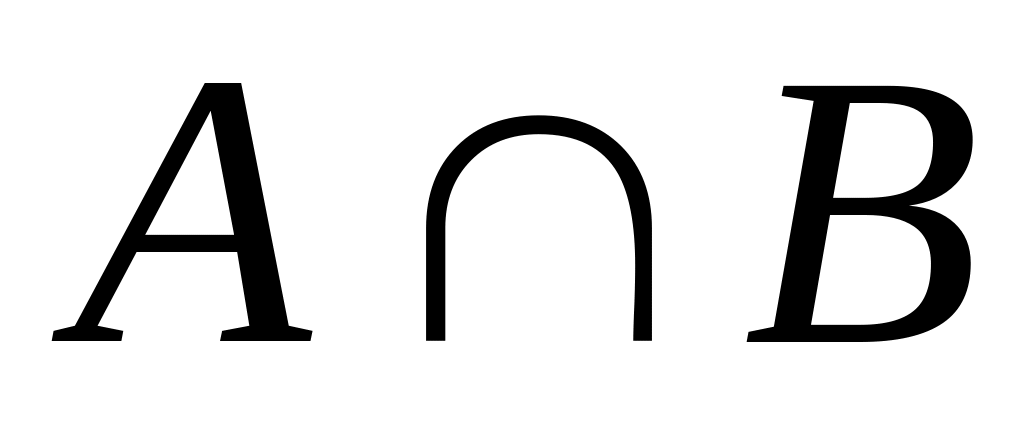 ;
;
 ;
;
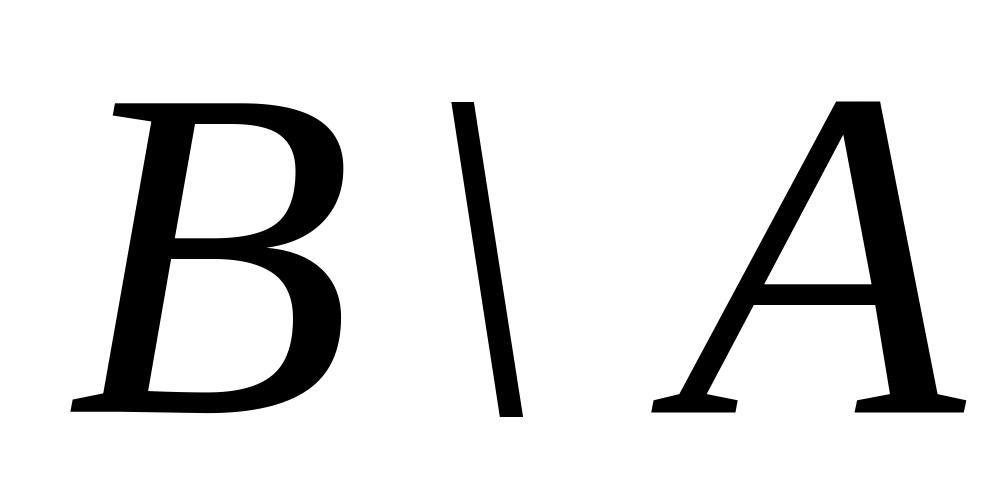 .
.Пусть А, В и С – множества такие, что
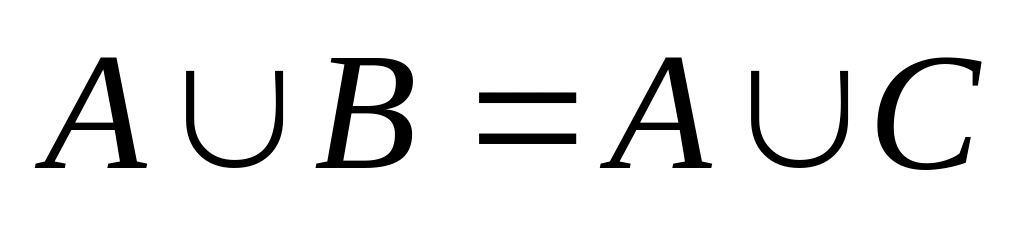 .
Можно ли сделать вывод, что В = С ?
.
Можно ли сделать вывод, что В = С ?Указать, какие из следующих равенств верны для любых множеств; верны для некоторых множеств; неверны или бессмысленны. Привести обоснование.
1) |
|
5) |
|
2) |
|
6) |
|
3) |
|
7) |
|
4) |
|
8) |
|
