Упражнения

Повторение

1. Упростить формулу с помощью эквивалентных преобразований. Получить дизъюнктивную нормальную форму (ДНФ). Привести формулу к СДНФ путем расщепления.

1. ;

2. ;

3. .

2. Разложить функцию по переменной х; у; z.

1. ;

2. ;

3. .

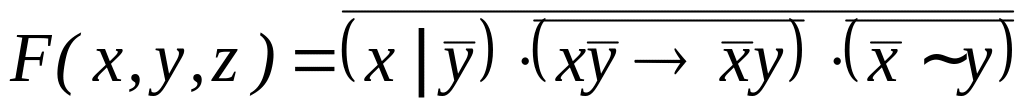3. Перейти от ДНФ к конъюнктивной нормальной форме (КНФ). Построить СКНФ (совершенную конъюнктивную нормальную форму) путем расщепления.

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

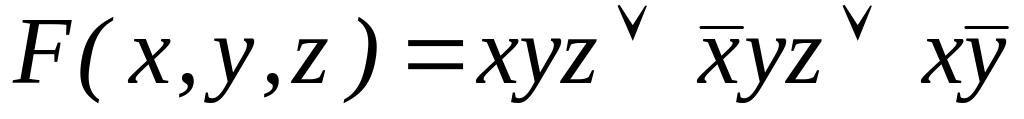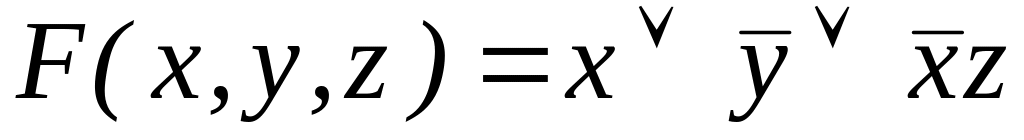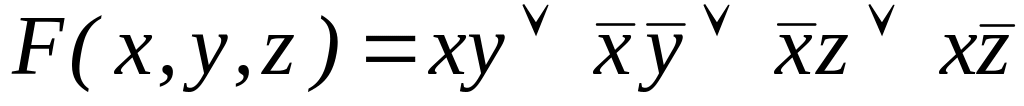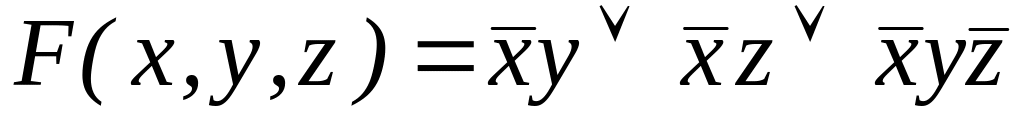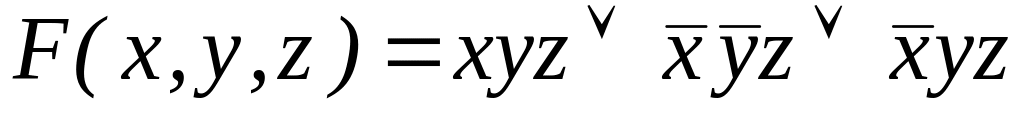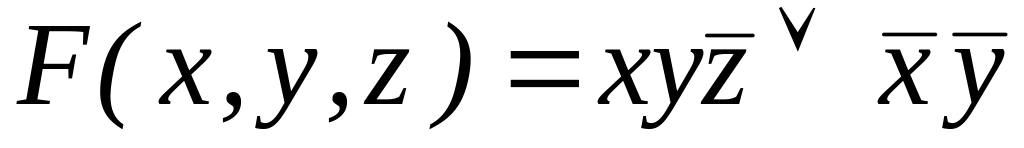1. Построить СКНФ с помощью вектор-столбца.

1. ;

2. ;

3. ;

4. .

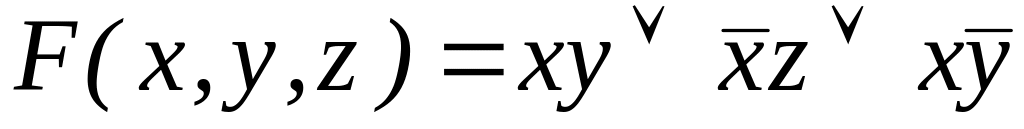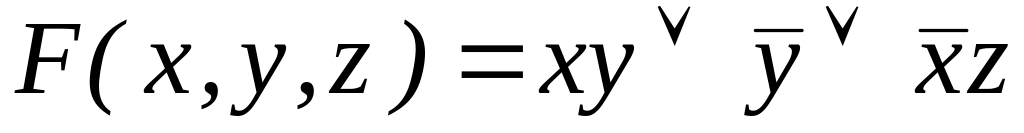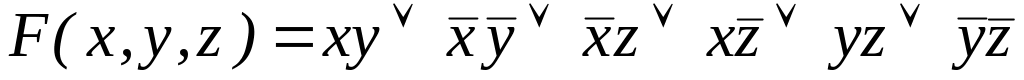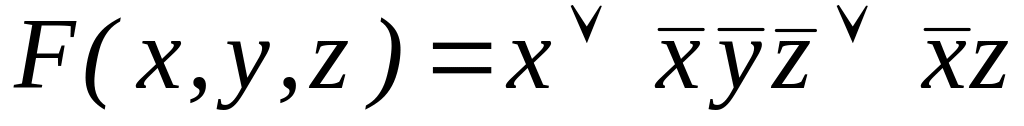4.4. Дизъюнктивные нормальные формы и импликанты

Функция f имплицирует функцию g, если .

Замечание: Если , то .

Если f имплицирует g, и f представлена единственной элементарной конъюнкцией, то f называется импликантом g.

Если из импликанта нельзя удалить ни одной переменной, то оно называется простым импликантом.

Теорема

Если функция представима единственной элементарной конъюнкцией

– всех n переменных, то ;

– переменных, то .

Пример.

Пусть . Она принимает значение 1 тогда и только тогда, когда x = 1, y = 1, z = 1. Значит .

Пусть . Она принимает значение 1 тогда и только тогда, когда y = 0, z = 1. Значит, чему равняется переменная х – неважно, и она может принимать любые значения. Поэтому .

Утверждение 1. Представление функции в виде ДНФ соответствует представлению ее единичного множества в виде объединения единичных множеств входящих в эту ДНФ элементарных конъюнкций.

Пример. Пусть функция представлена своей ДНФ.

.

Тогда ее единичное множество может быть представлено в виде:

.

Получилось, что .

Утверждение 2. Любая конъюнкция ДНФ функции является импликантом данной функции.

Утверждение 3. Если конъюнкция ДНФ функции не является простым импликантом, то можно найти соответствующий ей простой импликант (импликанты) и заменить им (их дизъюнкцией) непростой импликант.

ДНФ, состоящая только из простых импликантов, называется сокращенной.

Пример. Пусть функция представлена своей ДНФ.

.

Тогда ее единичное множество имеет вид:

.

Очевидно, что – это простой импликант. Он состоит из одной буквы, и если ее вычеркнуть, получится вырожденная конъюнкция (конъюнкция не имеющая переменных), что возможно только в случае, если .

Проверим, будет ли простым импликант .

Вычеркнем из него переменную х. Получим конъюнкцию . Ее единичное множество содержит 2 набора: , то есть по-прежнему является импликантом f. Значит – не простой импликант.

В свою очередь, полученный импликант является простым, так как вычеркивать из него буквы нельзя. Нельзя вычеркнуть – так как оставшаяся переменная z имеет единичное множество, содержащее 4 вектора с последней 1, а в таких векторов только 3; z – так как оставшаяся переменная имеет единичное множество, содержащее 4 вектора с 0 на втором месте, а в таких векторов только 3.

Значит, импликант – простой и им можно заменить в ДНФ исходный импликант .

Вычеркнем из k переменную . Получим конъюнкцию . Ее единичное множество содержит 2 набора: , то есть уже не является импликантом f.

Вычеркнем из него переменную z. Получим конъюнкцию . Ее единичное множество содержит 2 набора: , то есть также не является импликантом f.

Таким образом, ДНФ вида является сокращенной.