12. Среди пар графов, изображенных на рисунке, указать пары изоморфных графов и пары неизоморфных графов. Ответ обосновать.

    1)
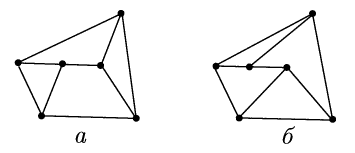
    2)

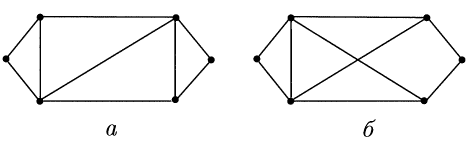
13. Задать различными способами, определенные ниже графы G. Определить их типы, построить дополнения , если 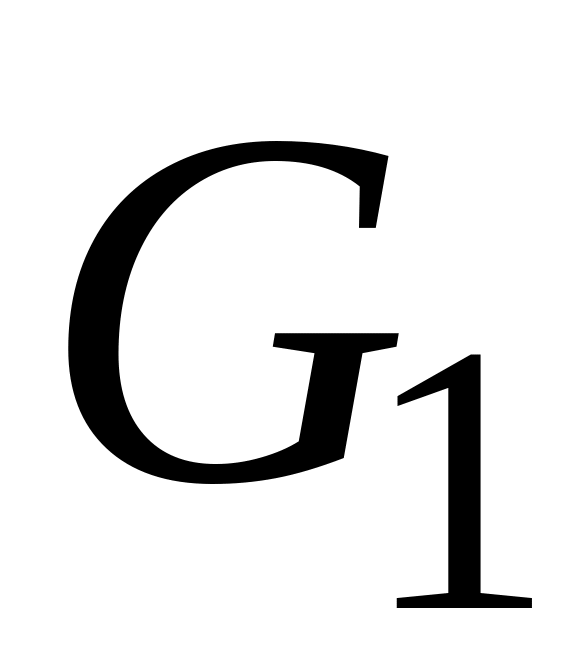– треугольник; 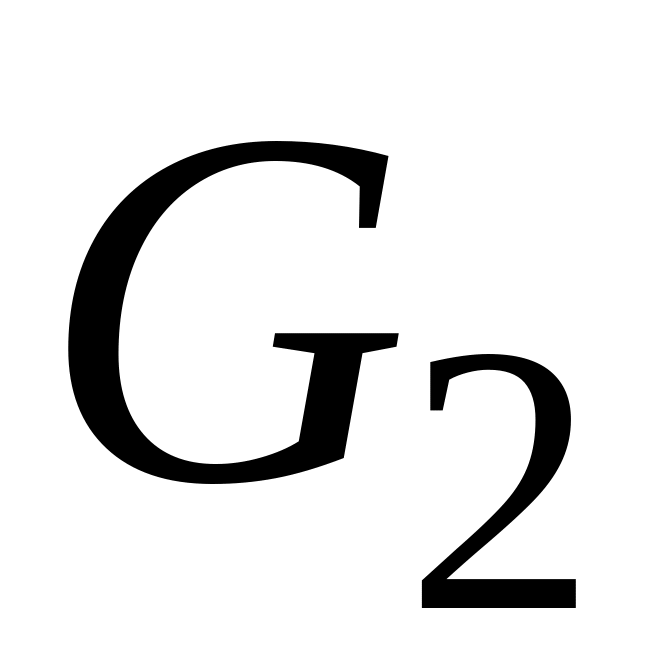– четырехугольник; 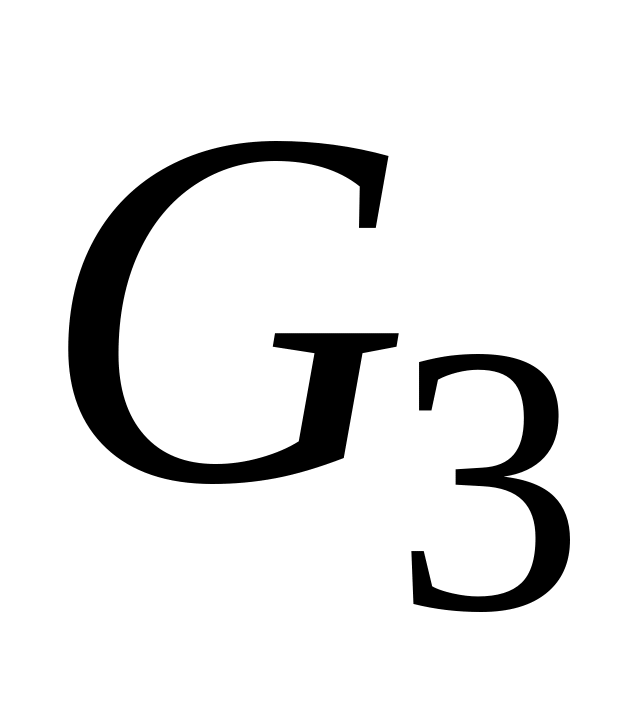– пятиугольник;

2. Маршруты, цепи и циклы. Расстояния, диаметры, центры. Обходы. Разделяющие множества и разрезы

Пусть G – конечный граф.

Маршрутом в G называется последовательность ребер, в которой каждые два соседних ребра имеют общую вершину:

_.

Число ребер в маршруте называется его длиной.

Маршрут, в котором совпадают начальная и конечная вершины, т.е. , называется циклическим (замкнутым).

Маршрут, в котором все ребра разные называется цепью (т.е. каждое ребро в нем встречается не более одного раза).

Цепь, в которой все вершины, кроме может быть первой и последней, разные называется простой цепью (т.е. каждая вершина и ребро в нем встречается не более одного раза).

Циклический (замкнутый) маршрут называется циклом, если он является цепью (т.е. все ребра в нем разные), и простым циклом, если эта цепь простая (т.е. и все вершины кроме первой и последней, разные).

Граф, не содержащий циклов, называется ациклическим.

Лемма: Если степень всех вершин в графе больше 1 (больше или равна 2), то граф обязательно содержит цикл.

Вершины и называются связными, если существует маршрут с началом в и концом в .

Утверждение: Связанные маршрутом вершины связаны также и простой цепью.

Утверждение: Отношение связности вершин графа является отношением эквивалентности и определяет разбиение множества вершин графа на непересекающиеся подмножества .

Граф называется связным, если для любых двух различных вершин существует цепь (маршрут, простая цепь), соединяющая их.

Граф G называется связным, если все его вершины связаны между собой. Очевидно, что все подграфы G(V_i) этого графа связны и называются связными компонентами графа.

Множество ребер, при удалении которых связный граф G становится несвязным, а несвязный граф увеличивает число компонент связности, называется разделяющим множеством. Минимальное разделяющее множество называется разрезом.

Ребро, при удалении которого граф перестает быть связным, называется мостом или перешейком.

Утверждение: Каждый н-граф распадается единственным образом в прямую сумму своих связных компонент .

Расстоянием d(v´, v´´) между .вершинами v´ и v´´ н-графа G называется минимальная длина простой цепи с началом v´ и концом v´´. или Расстоянием d(v´, v´´) между вершинами v´ и v´´ н-графа G называется длина кратчайшей (а, значит, простой) цепи с началом v´ и концом v´´.

Центром называется вершина н-графа, от которой максимальное из расстояний до других вершин являлось бы минимальным.

Максимальное расстояние от центра G до его вершин называется радиусом графа r(G).

Диаметром связного графа D(G) называется расстояние между двумя наиболее удаленными друг от друга вершинами.

Эйлеров цикл – цикл графа, без повторения ребер, обходящий все вершины графа. Эйлеров граф – граф, имеющий эйлеров цикл.

Теорема Эйлера: Конечный неориентированный граф G эйлеров тогда и только тогда, когда он связен и степени всех его вершин четны.

Эйлерова цепь (полуэйлеровый граф) – цепь, включающая все ребра данного конечного н-графа G, но имеющая различные начало v´ и конец v´´, т.е. это граф, в котором если существует маршрут без повторения ребер (эйлеров путь), обходящий все ребра графа ровно один раз.

Эйлеров (и полуэйлеров) граф можно считать следом пера, вычерчивающего этот граф, не отрываясь от бумаги)

Теорема Эйлера (2): Конечноый н-граф G будет полуэйлеровым (в нем существует эйлерова цепь), тогда и только тогда, когда он связный и четность степеней всех вершин, кроме начальной v´ и конечной v´´ (v´ и v´´должны иметь нечетные степени).

Чтобы в конечном орграфе существовал эйлеров цикл, необходимы и достаточны его связность, а также равенство степеней вершин этого графа по входящим и выходящим ребрам, т.е. ρ₁ (v) = ρ₂ (v), ∀ v ∈ G.

Алгоритм Флери нахождения эйлерова цикла:

Начиная с (любой) вершины нечетной степени, ”стираем” пройденные ребра, причем по мосту (перешейку) проходим только, если нет других возможностей.

Гамильтонов цикл – простой цикл, проходящий через все вершины рассматриваемого графа.

Гамильтонова цепь – простая цепь, проходящая через все вершины графа, с началом и концом в разных вершинах v₁, v₂ ∈ G.

Кратко рассмотрим проблему, связанную с возможным обходом всех вершин в графе: существует ли в данном (связном) графе цикл (или маршрут), обходящий каждую вершину (кроме первой) только один раз. Если такой цикл (маршрут) существует (в этом случае такой цикл будет контуром, а маршрут – путем), то граф называется гамильтоновым (полугамильтоновым), и соответствующий цикл (путь) также называют гамильтоновым циклом (путем). Несмотря на сходство постановки задач для гамильтоновых графов с эйлеровыми, “хорошего” решения для гамильтоновых графов нет. Вообще, о гамильтоновых графах известно очень мало. В основном – это теоремы типа “если в графе достаточное число ребер, то он гамильтонов”. Ясно, что теоремы такого типа не могут дать критерия гамильтонова графа, поскольку в графах такого типа вершин может быть очень много, а ребер сравнительно мало.

Приведем без доказательства самую известную теорему.

Теорема (Дирак, 1952). Если в связном графе с п вершинами (при n) степени всех вершин больше или равны п/2, то граф гамильтонов.