Упражнения
1. Определите
свойства соответствий между множествами
и
.
Какие из них являются функциями типа
1)
;
3)
;
2)
;
4)
.
2. Соответствие задано рисунком. Определить свойства соответствия. Является ли оно функцией, отображением?
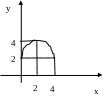
Рис 1. Рис.2. Рис.3.
Для рис. 1 определить:
1) образ 2; 2) образ 4; 3) образ [2; 4]; 4) образ (2; 4]; 5) прообраз 2; 6) прообраз 4; 7) прообраз [2;4]; 8) прообраз (0;4).
Для рис. 2 определить:
1) образ 2; 2) образ 4; 3) образ [2; 4]; 4) образ (4; 6]; 5) прообраз 0; 6) прообраз 4; 7) прообраз [0;4]; 8) прообраз (0;4).
Для рис. 1 определить:
1) образ 2; 2) образ 4; 3) образ [2; 4]; 4) образ (0; 4]; 5) прообраз 2; 6) прообраз 4; 7) прообраз [2;4]; 8) прообраз (2;4).
3. Определите
свойства соответствий между множествами
и
.
Какие из них являются функциями типа
1)
;
3)
;
2)
;
4)
.
Определите, какие из следующих подмножеств
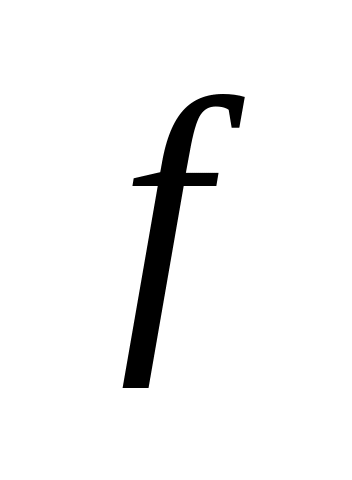множества
являются функциями
.
Объясните свой ответ.
1)
,
,
2)
,
Пусть
,
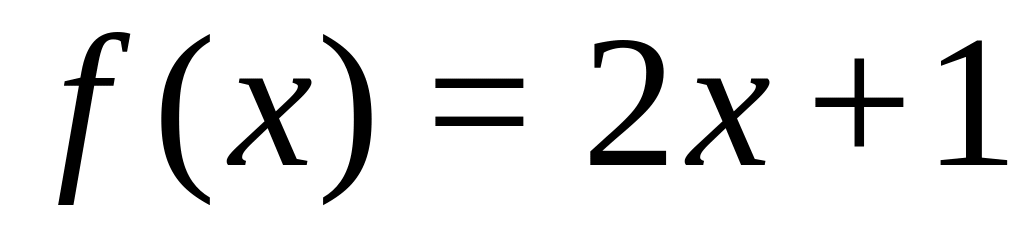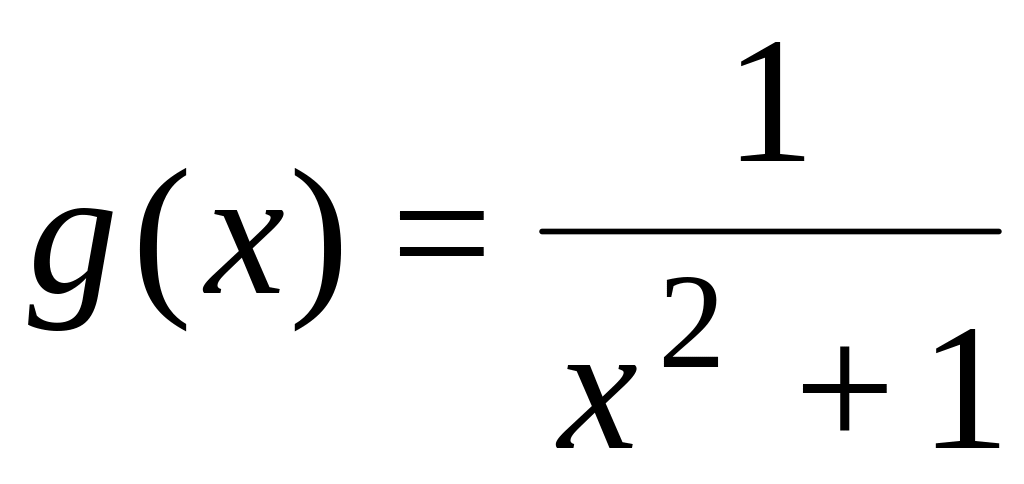– функции
.
Найдите:
1)
|
|
3)
|
2)
|
|
4)
|
;
;
;
.
Дано множество
и два
преобразования этого множества (т.е.
функции типа
):
и
или, как обычно принято записывать преобразования конечных множеств:
и
.
Найти композиции
преобразований:
и
.
7. Найти композиции преобразований: и , если
1)
и
;
2)
и
;
3)
и
.
Пусть тип функции . Для различных А, В и f определить область определения и область значения. Будут ли у этих функций обратные? Если да, то будут ли они отображениями. Сделайте вывод о том, какими свойствами должна в этом случае обладать функция.
1)
,
если а) А=R;
В=R;
б) A=N;
В=N.
2)
,
если а) А=R+;
В=R;
б) A=N0;
В=N.
3)
,
если а) А=R;
В=R;
б) A=R+;
В=R.
4)
,
если а) А=R;
В=R;
б) A=R+;
В=R+.
5)
,
если а) А=R;
В=R;
б)
A=
;
В=[0; 1].
Определить область определения и область значений композиций и .
1)
;
;
г)
;
;
2)
;
;
д)
;
;
3)
;
;
е)
;
.
10. Найти композиции преобразований: и , если
1)
и
;
2)
и
;
3)
и
.
11. Найти композиции
,
,
и
,
если
и
функции типа
.
1)
=
;
2)
=
;
3)
=
;
4)
=
.
1.6. Отношения
Подмножество
называется n
- местным
отношением
на множестве М.
Говорят, что
находится в отношении R,
если
.
Одноместное
отношение
– это просто подмножество М. Такие
отношения называют признаками: элемент
а
– обладает признаком R,
если
и
.
Свойства одноместных отношений это свойства подмножеств М, поэтому для случая n = 1 термин “отношение” употребляется редко.
Примером трехместного (тернарного) отношения является множество троек нападающих в хоккейной команде. Любой из нападающих находится в этом отношении со всеми теми игроками, с которыми он играет в одной тройке (один нападающий может, вообще говоря, участвовать более, чем в одной тройке).
При n = 2 – отношения называются двуместными или “бинарными”. Если a, b находятся в отношении R, это записывается aRb.
Пусть дано отношение
R
на М.
Для любого подмножества
естественно определяется отношение
,
называемое сужением
R на
,
которое получается из R
удалением всех пар, содержащих элементы,
не принадлежащие
.
Иначе говоря,
.
Строго говоря, R
и
это разные отношения с разными областями
определения.