
8.4. Понятие о следящем электроприводе
Основное отличие следящего электропривода от систем точного позиционирования состоит в постановке задачи регулирования: обеспечение следования (слежения) положения исполнительного органа механизма φ'за изменяющимсяпопроизвольному закону положением задающего органа <рз с ошибкой, во всех режимах работы не превышающей допустимого .значения. Поэтому рассмотренная выше трехконтурная система регулирования положения представляет собой следящий электропривод в тех случаях, когда замыкание электропривода, например по углу поворота исполнительной оси установки, имеет целью воспроизведение произвольно меняющегося угла поворота задающей оси, т. е. слежение исполнительной оси за движением задающей оси, с заданной точностью. При этом отработка заданного скачком угла поворота, т. е. рассмотренная выше отработка дозированных перемещений, является частным режимом работы следящего электропривода.
Воспроизведение с высокой точностью произвольных законов движения, задаваемых перемещением задающей оси `З(t), является одной из наиболее сложных задач автоматизированного электропривода. Произвольность движения задающей оси определяет исключительное многообразие условий работы электропривода, при котором проявляется влияние существенных нелинейностей системы, таких, как сухое трение при движении с малой знакопеременной скоростью, кинематические зазоры при движении со знакопеременным моментом двигателя и т. п. Высокие требования к точности воспроизведения угла поворота задающей оси требуют особо тщательного синтеза динамических качеств электромеханической системы, причем их удовлетворение сильно осложняется отмеченным ранее влиянием нелинейностей и наличием в системе упругих механических связей.
Ограничимся анализом динамической точности следящего электропривода с линейными жесткими механическими связями. Для этого получим изображение ошибки в трехконтурной системе, структурная схема которой показана на рис. 8.4, с помощью общей формулы ошибки (5.19):
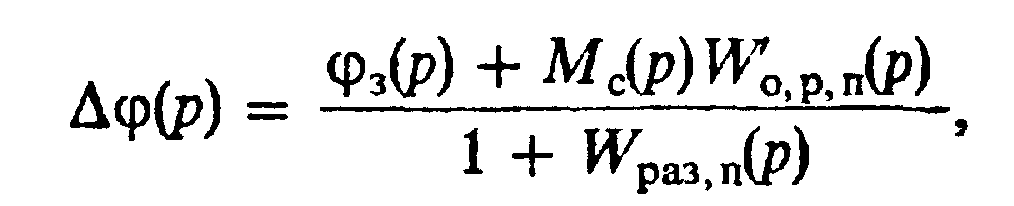 (8.30)
(8.30)
где W`o.р.п- передаточная функция объектарегулирования положения по возмущениюМс(р).
Для определения этой передаточной функции представим структурную схему рис. 8.4 в виде, показанном на рис. 8.7, пренебрегая внутренней связью по ЭДС и принимая kО.П=1. На основании этой схемы можно записать
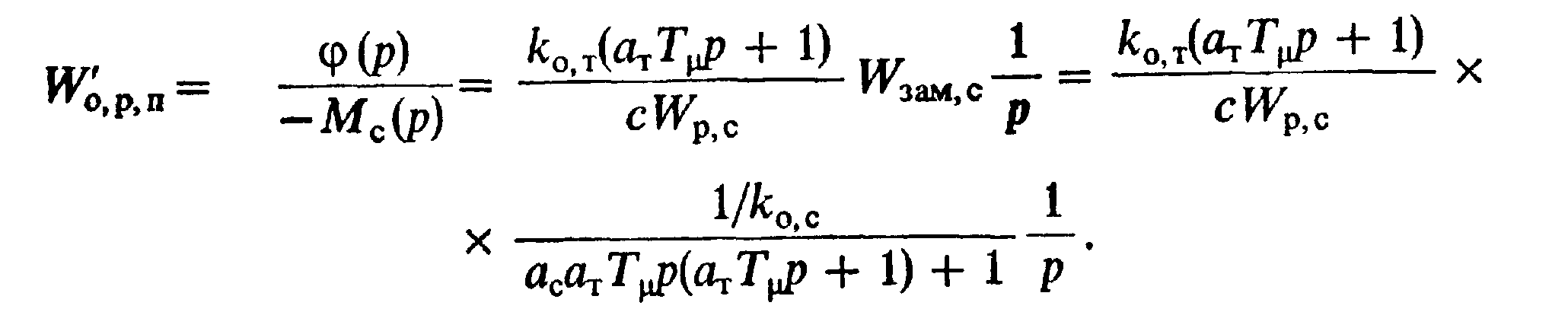 (8.31)
(8.31)
Подставляем (8.31) в (8.30), выражаем Wp.спомощью (7.39) и учитываем, что приkР.П=1`З=З. В результате преобразований получаем
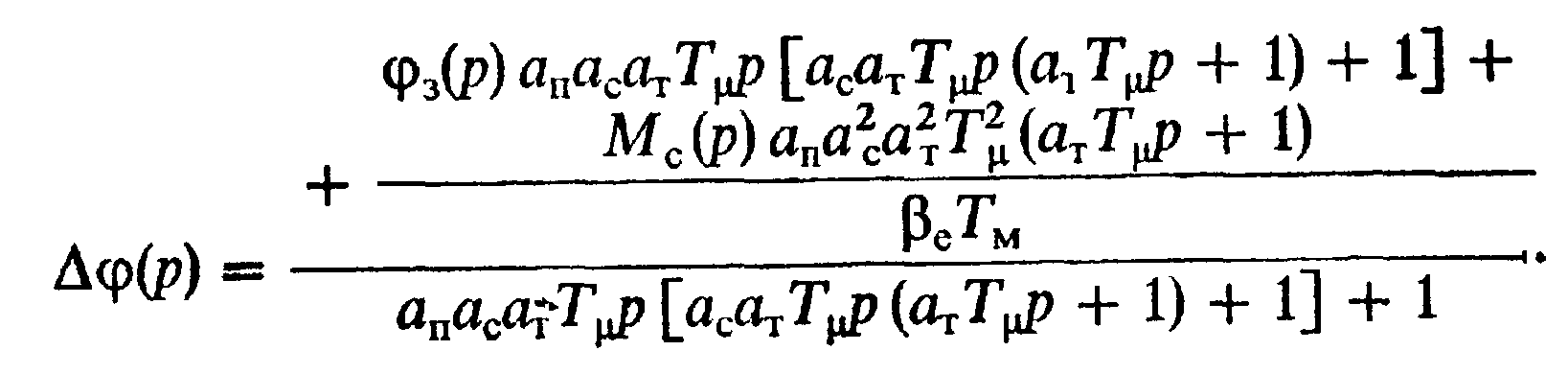 (8.32)
(8.32)
Рассматривая (8.32), можно установить, что статическая ошибка системы определяется только действием постоянной нагрузки Мс и не зависит от задающего сигнала. Статическая ошибка определяется формулой (8.27), которая вытекает из (8.32) при ρ=0 и которая была уже получена из физических представлений.
Важной оценкой динамической точности следящего электропривода является установившаяся ошибка в режиме отработки линейного нарастания задающего сигнала З(t)=ωЗ(t)=ωЗ/р, которую нетрудно определить, подставив это изображение
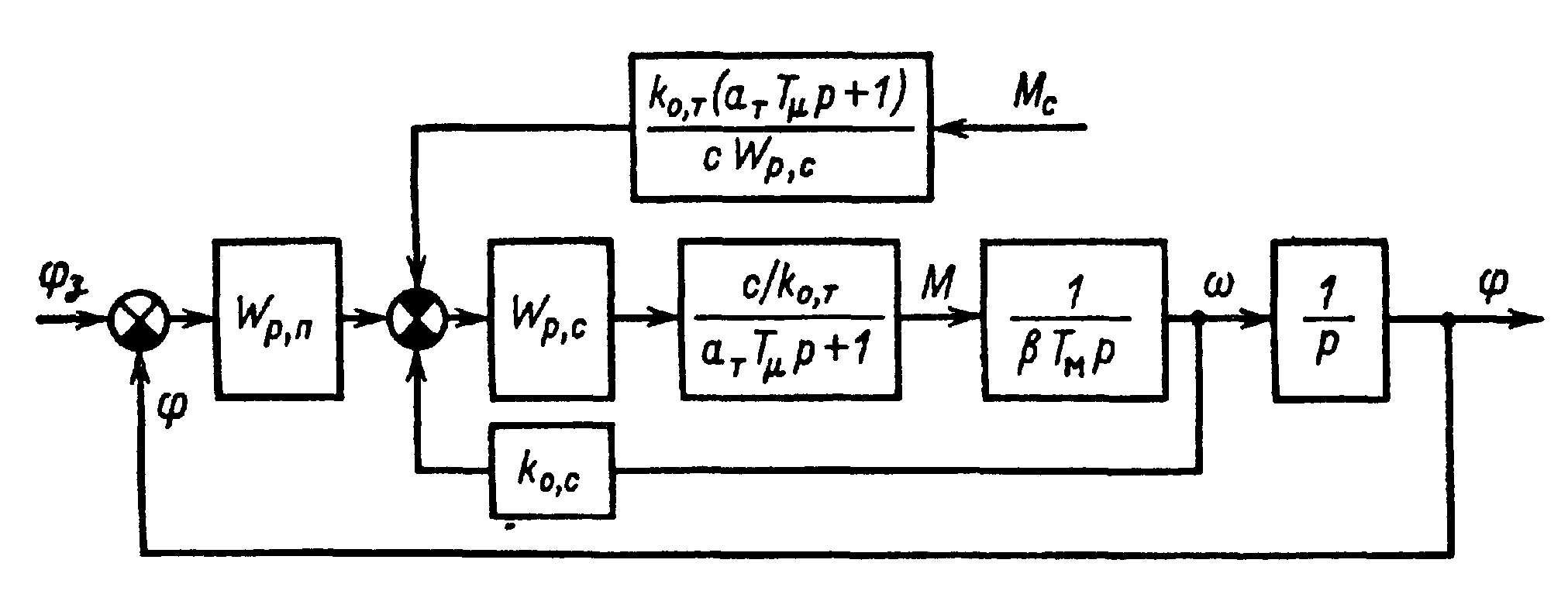
Рис. 8.7. Преобразованная структурная схема трехконтурной системы следящего электропривода
задающего сигнала в (8.32):
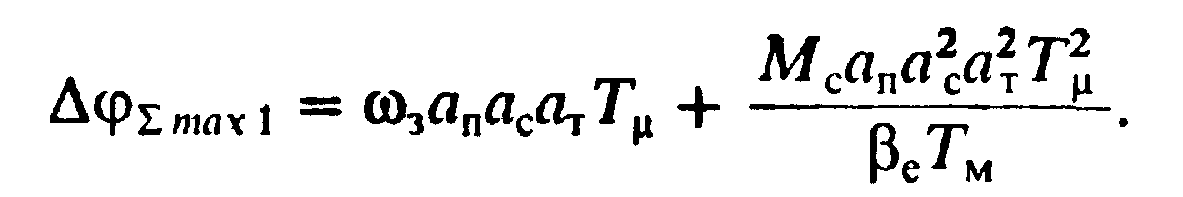 (8.33)
(8.33)
Рассматриваемый режим есть режим движения следящего электропривода с постоянной скоростью ωЗ, задаваемой вращением задающей оси. Полученное выражение (8.23) свидетельствует о том, что в этом режиме ошибка складывается из двух составляющих. Первая составляющая называется скоростной ошибкой ΔφMAX1,которая пропорциональна скорости и зависит только от некомпенсируемой постоянной контура регулирования положения ТμП=аСаТТμ и от соотношения постоянных этого контурааП:
(8.34)
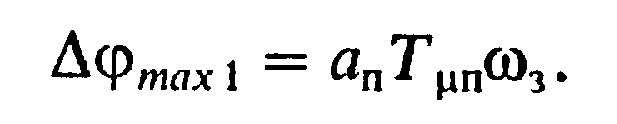
Вторая составляющая представляет собой статическую ошибку ΔСи при данной нагрузке Мс=constзависит от тех же факторов и от модуля статической жесткости в двухконтурной статической системе регулирования скорости βЗ.С:
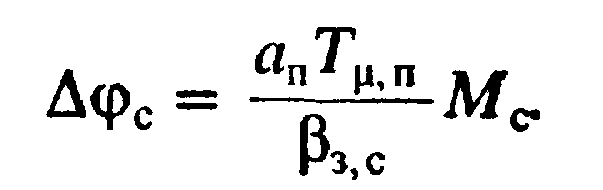 (8.35)
(8.35)
Передаточную функцию разомкнутой системы при kОП=1 можно представить в виде
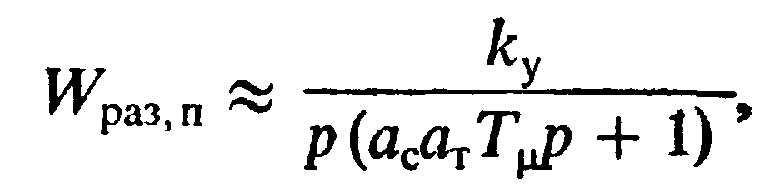 (8.36)
(8.36)
где ky=1/aПΤμ.п —коэффициент усиления разомкнутого контура регулирования положения.
Учитывая (8.36), выражение скоростной ошибки (8.34) можно записать в более общем виде:
![]() (8.37)
(8.37)
Соответственно выражение статической ошибки (8.35) имеет вид
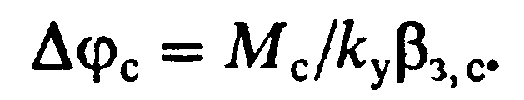 (8.38)
(8.38)
Следовательно, при данной скорости заводки ω3уменьшение скоростной ошибки обеспечивается только увеличением коэффициента усиления разомкнутой системыky,т. е. в данном случае выбором наименьших допустимых по критерию качества регулирования коэффициентов аП, аС, и аТпри данной сумме некомпенсируемых постоянных Тμв контуре регулирования тока. Статическая ошибка зависит как от коэффициента усиления контура регулирования положения, так и от жесткости статических механических характеристик системы при разомкнутой связи по положению. В рассматриваемой системе, оптимизированной методом последовательной коррекции, жесткостьз,сзависит от отношенияеТм/аcaтТ, поэтому уменьшение ап.,аси атснижает статическую ошибку вследствие возрастания коэффициента усиления и увеличения жесткостиз,с. В соответствии с (8.38) статическая ошибка может быть полностью устранена при использовании двукратноинтегрирующего контура регулирования скорости при ПИ-регулягоре скорости.
Обратим внимание на то, что если момент нагрузки Мссодержит составляющую вязкого тренияв,т, то статическая ошибка в установившемся режиме движения с постоянной скоростью заводки в соответствии с (8.38) будет содержать составляющую, пропорциональную скорости и увеличивающую скоростную ошибку на значение, равное:
![]()
Динамические ошибки в неустановившихся режимах движения могут дополнительно увеличиваться из-за переходных составляющих. Так, при уменьшении ап.,аси атколебательность системы увеличивается, переходные составляющие ошибки могут возрастать, в то время как установившаяся динамическая ошибка (8.33) при этом уменьшается. Поэтому выбор ап.,аси атдолжен обеспечить минимум полной динамической ошибки во всех режимах.
Для того чтобы при произвольном входном сигнале иметь возможность конкретизировать требования к динамической точности, задают максимальные расчетные значения первой и второй производных входного сигнала maxиmax = (d3 /dt). Для расчетных режимов заводки с постоянной скоростью3 = constи с линейно возрастающей скоростью3 = 3tвводятся понятия добротности по скорости
![]() (8.39)
(8.39)
и добротности по ускорению
![]() (8.40)
(8.40)
где max доп— допустимая ошибка слежения.
Эти параметры позволяют построить граничную ЛАЧХ в области низких частот, которая обеспечивает в этой области значения динамических коэффициентов усиления L(), достаточные для ограничения ошибки допустимым значением для гармонического входного сигнала=maxsintпри условииоmaxи<max. Построение этой ЛАЧХ, как показано на рис. 8.8, сводится к построению прямой1 снаклоном -20 дБ/дек, пересекающей ось абсцисс в точке=kи прямой 2, пересекающей ту жеось в точке==k. Для обеспечения требуемой динамической точности слежения ЛАЧХ разомкнутого контура регулирования положения не должна заходить в область, граница которой отмечена на рис. 8.8 штриховкой.
Рассмотренная трехконтурная система следящего электропривода настроена на точную компенсацию постоянных, и ее ЛАЧХ (прямая 3)в низко- и среднечастотной областях имеет наклон-20дБ/дек, как и прямая1.Очевидно, эта настройка может обеспечить требуемую точность регулирования, если заданная добротность по скоростиk, меньше частоты среза системы или равна ей:
![]() (8.41)
(8.41)
При настройке всех контуров на технический оптимум aп=ас= ат= 2 и Т=0,01 с заданное значениеkне должно превышать 12,5. На практике требуются коэффициенты добротности по скорости на порядок большие, поэтому рассмотренная система в применении к следящему электроприводу обладает ограниченными возможностями.
Вид граничной по условиям точности регулирования ЛАЧХ (отмеченной на рис. 8.8 штриховкой) свидетельствует о целесообразности использования контура регулирования, настроенного на симметричный оптимум. Пусть при заданной добротности по скорости kи ускорениюkЛАЧХ трехконтурной системы с П-регулятором положения имеет вид, показанный на рис. 8.8 ломаной3.Заменив П-регулятор положения ПИ-регулятором и подобрав параметры по симметричному оптимуму, получим
![]() (8.42)
(8.42)
Передаточной функции (8.42) соответствует ЛАЧХ с частотой среза с= 1/8 Ти низкочастотной асимптотой, имеющей наклон — 40 дБ/дек (прямая4на рис, 8.8). Сравнивая прямые3
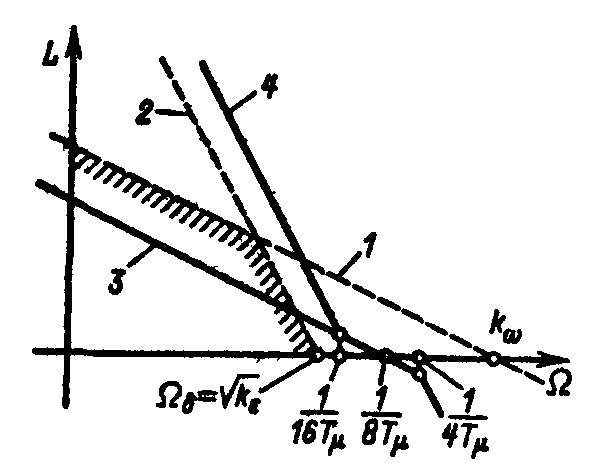
Рис.8.8 . Варианты ЛАЧХ следящего электропривода
и 4,можно убедиться, что использование симметричного оптимума может обеспечивать выполнение требований к точности в случаях, когда настройка на технический оптимум дает недостаточные для этого коэффициенты усиления в области низких частот. Дополнительное увеличение динамической точности регулирования может быть достигнуто путем использования в качестве подчиненного контура регулирования астатической одноконтурной системы регулирования скорости с ПИД-регу-лятором скорости.
Реализация такой системы существенно упрощается в тех случаях, когда постоянная Тядостаточно мала и может быть отнесена к некомпенсируемым постоянным без значительного увеличения Т. В подобных случаях тот же эффект достигается при более помехоустойчивом ПИ-регуляторе скорости.
