
Васильев К.К. Теория автоматического управления (следяшие системы)
.pdf
|
n(t) |
|
|
g(t) |
z(t) |
z1(t) |
x(t) |
|
+ |
H1(jω) |
H2(jω) |
|
|
Рис. 36 После этого с помощью уравнения Винера найдем переда-
точную функцию H2(jω) и выделим ее реализуемую часть H2P(jω). Общая передаточная функция оптимальной реализуемой системы запишется в виде: W(jω)=H1(jω) H2P(jω).
Каким же образом превратить z(t) в белый шум с помощью фильтра? Нам известен энергетический спектр Gz(ω)=Gg(ω)+Gn(ω). Необходимо, чтобы Gz (ω) H1 ( jω)2 = N1 , где N1 - спектральная плот-
ность белого шума z1 , например, N1 =1. Запишем это выражение по-другому. Представим энергетический спектр Gz(ω) в виде произведения Gz (ω) =ψ ( jω)ψ (− jω) , а H1 ( jω)2 = H1( jω)H1(− jω) . Тогда требуется, чтобы
ψ ( jω)ψ (− jω) H1 ( jω) H1 (− jω)=1.
Для этого необходимо выбрать фильтр с передаточной функцией H1 ( jω) =1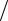 ψ ( jω). Такой фильтр превращает входное воздейст-
ψ ( jω). Такой фильтр превращает входное воздейст-
вие в белый шум и называется обеляющим. Заметим, что введение обеляющего фильтра не приводит к потере оптимальности системы. Действительно, всегда можно восстановить входной сигнал с помощью фильтра с передаточной функцией H1 ( jω). Вместе с тем,
преобразование z(t ) в белый шум z1 (t ) позволяет построить опти-
мальную реализуемую систему. Для этого из уравнения Н.Винера найдем передаточную функцию H2 ( jω) оптимальной нереализуе-
мой системы, выделим реализуемую часть и в результате получим оптимальный реализуемый фильтр Винера. Наиболее просто это осуществляется, если помеха n(t) является белым шумом со спектральной плотностью N0.
Тогда передаточная функция оптимального реализуемого
фильтра записывается в виде W P ( j ω ) = 1 − |
N 0 |
. Для по- |
|
ψ ( j ω ) |
|
строения такого фильтра достаточно представить энергетический спектр Gz(ω)=Gg(ω)+N0 в виде произведения двух комплексно-
61

сопряженных сомножителей G z (ω) = ψ( jω)ψ(− jω) и воспользо-
ваться записанной формулой для передаточной функции оптимальной реализуемой системы управления.
Пример 2. |
Пусть R g (τ) = σg2e−a |
|
τ |
|
, Gg (ω) = |
|
2aσg2 |
, |
G n (ω) = N0 . |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
w 2 + a 2 |
|||||||||||||||||||||||||||||||
Разложим Gz (ω) = Gg (ω) + Gn (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
на комплексно-сопряженные множи- |
|||||||||||||||||||||||||||||||||||||
тели: |
|
|
|
|
|
|
|
|
2aσg2 |
|
|
|
|
|
|
|
|
|
|
ω2 |
+a2 (1+2q) |
|
|
|
|
|
|||||||||||
|
|
G (ω) = |
|
+ N |
|
= N |
|
|
|
= |
|
|
|
|
|||||||||||||||||||||||
|
|
ω2 |
+a2 |
|
|
|
|
|
|
|
|
ω2 +a2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
= N0 |
|
a 1+ 2q + jω |
|
N0 |
|
|
a 1+ 2q − jω |
. |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
a + jω |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a − jω |
|
|
|
|
|
|
|
|
|
||||||
Таким образом, |
ψ( jω) = |
|
N0 |
a |
1+ 2q + jω |
|
. Найдем теперь переда- |
||||||||||||||||||||||||||||||
|
|
a + jω |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
точную функцию оптимального реализуемого фильтра: |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
N |
0 |
|
|
|
|
|
a |
+ ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2q |
|
|
|
|
|
||||
W ( jω) =1− |
|
|
|
|
=1− |
|
j |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||||
ψ( jω) |
|
|
+ |
|
+ ω |
|
|
|
+ |
|
+ |
|
|
+ |
|
|
+ ω |
||||||||||||||||||||
P |
|
|
|
|
|
a 1 |
2q |
|
|
|
1 |
2q( 1 |
2q |
1)(1 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
j T) |
|
||||||||||||
где T = |
|
1 |
|
|
. Импульсная характеристика такого фильтра оп- |
||||||||||||||||||||||||||||||||
a |
1+2q |
||||||||||||||||||||||||||||||||||||
ределяется с помощью обратного преобразования Фурье:
h(τ) = |
2aq |
e−a 1+2q τ , τ ≥ 0. |
1 |
+ 2q +1 |
|
Точно так же, как и раньше, может быть найдена минимально достижимая дисперсия ошибки реализуемой системы:
σ0P2 |
= N0 h(0) = |
2aqN |
|
= |
2σg2 |
||
1+ 2q |
0 |
. |
|||||
|
|
|
|
+1 |
|
1+ 2q +1 |
|
Заметим, что найденная дисперсия ошибки σOP2 больше, чем |
|||||||
дисперсия ошибки |
σo2min = |
σ 2 |
|
|
|
||
1 |
g |
нереализуемой системы управле- |
|||||
|
|
+ |
2q |
|
|
|
|
ния (см. пример 1).
Таким образом, подход Винера хотя и с дополнительными усложнениями, но все-таки дает возможность построения физически реализуемой системы управления и определения ее точностных характеристик для стационарных входных воздействий и бесконечного времени наблюдения.
62

Фильтр Калмана для стационарных процессов
Полученное в последнем примере решение задачи синтеза оптимальной реализуемой системы дает возможность определить импульсную переходную характеристику h(τ ) или передаточную
функцию Wp ( jω). Вместе с тем, существует еще одна форма пред-
ставления оптимальной системы с помощью дифференциального уравнения. На это обстоятельство в 1959 г. обратил внимание Р. Калман. Помимо простоты реализации оптимальных САУ для определенного, но достаточно широкого класса входных сигналов, метод Р. Калмана позволяет произвести синтез оптимальных многомерных нестационарных САУ.
Рассмотрим вначале возможности описания оптимальной системы, с помощью дифференциального уравнения. Как было установлено, передаточная функция оптимальной реализуемой системы управления записывается в виде:
|
|
|
|
WP ( jω) = |
|
|
|
2q |
|
|
|
|
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1+ |
2q( 1+ 2q +1)(1+ jωT ) |
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
T = |
|
|
|
. При этом выходной сигнал |
||||||||||||||||
a 1+ 2q |
|||||||||||||||||||||
|
|
|
|
|
|
|
x( p) =WP ( p)z( p) |
|
|
или |
|||||||||||
|
|
|
x( p) = |
|
|
|
|
|
|
2q |
|
|
|
z( p) . |
|||||||
|
|
|
|
1+ 2q( |
1+ 2q +1)(1+ pT ) |
||||||||||||||||
|
После несложных преобразований: |
|
|
|
|
|
|||||||||||||||
|
|
x( p) + pTx( p) = |
|
|
|
2q |
|
|
|
z( p), |
|||||||||||
|
|
|
|
1+ 2q( |
1+ 2q +1) |
|
|||||||||||||||
|
|
|
dx(t) |
|
+ |
|
1 |
x(t) = |
|
|
2q /T |
|
|
|
z(t), |
||||||
|
|
|
|
dt |
|
|
|
1+ 2q( 1+ |
|
|
|
||||||||||
|
|
|
|
|
|
T |
|
|
2q +1) |
||||||||||||
|
|
|
|
dx(t) |
+ ax(t) = |
|
|
2aq |
|
(z(t) − x(t)), |
|||||||||||
|
|
|
|
dt |
( |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
1+ 2q +1) |
|
|
|
|
|
|||||||
получим следующее дифференциальное уравнение, описывающее оптимальную систему:
dxdt(t) = −ax(t) +VN0−1(z(t) − x(t)),
63

где |
V =σ02P = |
|
2σ 2 |
Такую систему можно представить с |
|
|
g . |
||||
|
|
1+ 2q +1 |
|
|
|
помощью структурной схемы на рис.37, где K=VN0-1 . |
|||||
|
|
n(t) |
|
|
|
|
g(t) |
+ |
z(t) + |
+ |
x(t) |
|
|
|
- |
К |
t ∫ |
|
|
|
- |
0 |
|
|
|
|
|
||
|
|
|
|
|
a |
Рис. 37 Эта структурная схема и является решением Калмана рассматри-
ваемой задачи. Оказывается, процедуру оптимального управления можно представить в виде системы с обратной связью. Очень важно, что структура не изменяется и остается оптимальной, если изменяются параметры сигналов и помех, а также на этапе переходного процесса. В этих случаях оптимальная система (рис. 37) становится системой с переменными параметрами k=k(t) и a = a(t).
Р. Калман обратил также внимание, что часть системы управления полностью определяется видом входного сигнала. Дей-
ствительно, если спектр входного воздействия Gg (ω) = |
2aσg2 |
, то та- |
|
ω2 + a2 |
|||
|
|
кое воздействие может быть сформировано из белого шума ξ(t) с помощью фильтра, описываемого дифференциальным уравнением
dgdt(t) + ag(t) = aξ(t) .
Найдем величину Nξ энергетического спектра белого шума ξ (t ), обеспечивающего формирование сигнала g (t ) с заданным спектром Gg (ω)= 2aσg2  (ω2 + a2 ). После преобразования по Лап-
(ω2 + a2 ). После преобразования по Лап-
ласу дифференциальное |
уравнение |
запишется |
в виде |
||||||||||||||
|
pg + ag = aξ( p) |
– энергетический спектр. |
При этом передаточная |
||||||||||||||
функция |
соответствующего фильтра |
Hϕ ( p) = |
a |
|
или |
||||||||||||
p + a |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Hϕ ( jω) |
|
2 = |
a2 |
. |
Таким образом, |
спектр сигнала |
g (t ) |
на выходе |
||||||||
|
|
||||||||||||||||
|
|
ω2 + a2 |
|||||||||||||||
фильтра |
|
|
|
|
|
2 = |
Nξa2 |
, т.е. для полного соответствия |
|||||||||
Gg (ω) = Nξ |
|
Hϕ ( jω) |
|
||||||||||||||
|
|
||||||||||||||||
|
|
w2 +a2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
64

спектру входного воздействия достаточно выбрать Nξ a2 = 2aσg2
или Nξ = 2σ g2  a .
a .
С другой стороны, рассмотренное дифференциальное уравнение можно представить как уравнение, описывающее систему с обратной связью, показанную на рис. 38.
a
ξ(t) |
+ |
g(t) |
Х |
t |
∫ |
- |
0 |
a
Рис. 38 Сравним структурные схемы оптимальной САУ (рис. 37) и
полученной системы (рис.38), формирующей входной сигнал g(t) . Анализ структурных схем и связанных с ними дифференциальных уравнений показывает полное соответствие формирующего фильтра и значительной части структуры оптимальной САУ.
* * *
Таким образом, Р.Калман предложил другое представление для решения задачи построения оптимальной системы управления, данной Н.Винером. Но это представление решения в виде замкнутой системы, близкой по виду к формирующему фильтру, имело далеко идущие последствия. Было установлено, что структура системы управления не изменяется и при управлении одновременно несколькими параметрами, а также при нестационарных воздействиях. Эта структура сохраняется и остается оптимальной для широкого класса возможных входных сигналов и помех.
3.3. МНОГОМЕРНЫЕ ОПТИМАЛЬНЫЕ СИСТЕМЫ
Вначале подытожим основные результаты, полученные при решении задачи синтеза одномерной оптимальной реализуемой системы управления.
65

Пусть входное воздействие g(t) представляется реализацией случайного процесса с энергетическим спектром Gg (ω) = ω22aσ+ga22 и в
сумме z(t)=g(t)+n(t) с белым шумом (помехой) n(t) поступает на систему управления. В соответствии с методом Винера оптимальная реализуемая система имеет передаточную функцию
|
|
|
W ( jω) =1 − N0 |
= |
|
|
2q |
, |
|
|
|
|
P |
ψ( jω) |
|
1 + 2q ( 1 |
+ 2q +1)(1 + jωT) |
||
|
|
|
|
|
|||||
где q = |
|
σ2 |
, x(jω)=WP(jω)Z(jω). |
|
|
|
|||
|
g |
|
|
|
|||||
|
N0a |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Р.Калман предложил другое представление того же решения |
||||||||
в виде дифференциального уравнения |
|
dx(t) |
= −ax(t) + VN0−1(z(t) − x(t)) . |
||||||
|
dt |
||||||||
|
|
|
|
|
|
|
|
|
|
При этом входное воздействие g(t) удобно представить в виде выходного сигнала фильтра (рис.38), описываемого дифференци-
альным уравнением dgdt(t) = −ag(t) +ξ(+t) .
Фильтр, с помощью которого моделируется входное воздействие g(t), обычно называют формирующим фильтром. Само же входное воздействие g(t) при этом является состоянием формирующей системы.
Было установлено, что при описании входных сигналов в виде состояния некоторой системы всегда получается решение в виде точно такой же по виду системы с обратной связью. При этом структура САУ сохраняется для любого интервала времени, в том числе и во время переходного процесса, при изменении коэффициентов во времени, а также в случае, когда x(t) является век-
тором, т.е. при одновременном управлении по нескольким параметрам. И во всех этих случаях структура системы управления оказывается оптимальной в смысле минимума дисперсии ошибки
σ20 (t) = M{x(t) − g(t))2 }.
Вэтом разделе вначале рассматриваются математические модели входных многомерных нестационарных воздействий. После этого обсуждается структура оптимальной многомерной системы, которая называется фильтром Калмана.
66

Описание входных воздействий
Пусть нам необходимо осуществлять управление одновременно n выходными сигналами системы x1(t),..., xn (t). При этом мы
хотим получить наименьшие отличия этих сигналов от заданных
|
|
g (t |
функций – входных воздействий |
|
1 |
|
||
g(t) = ... |
||
|
|
|
|
|
gn (t |
)
. Будем описывать
)
входные воздействия с помощью системы линейных дифференциальных уравнений состояния:
|
|
|
|
|
|
|
|
|
|
|
dg(t) |
= A(t) |
|
(t) + V(t) |
|
(t) , |
|||
|
g |
ξ |
|||||||
|
|
dt |
|||||||
|
|
a11 (t) ... |
a1n (t) |
||||||
|
|
|
|
||||||
где A(t) – (n × n) – матрица: a21 (t) ... |
a2n (t) |
||||||||
|
|
|
|
... ... ... |
|||||
|
|
|
|
|
ann (t) |
||||
|
|
|
|
an1 (t) ... |
|||||
|
|
|
ξ1 (t) |
|
|
|
|
||
; |
|
(t) = |
... |
– век- |
ξ |
||||
|
|
|
|
|
|
|
ξm (t) |
|
|
|
|
|
торный белый шум с энергетическим спектром каждой компоненты Nξ1(t), Nξ2 (t),..., Nξm (t) соответственно.
v11(t) |
|
v |
(t) |
V(t) - (n × m)-матрица V(t)= 21 |
|
... |
|
|
(t) |
vn1 |
|
... v1n (t) |
|
|
... |
v (t) |
|
|
2n |
. |
... |
... |
|
... |
vnn (t) |
|
|
||
Рассмотрим примеры.
Пример 1. Уравнение состояния для трех независимых параметров.
Предположим, что необходимо обеспечить измерение траектории по 3 координатам, не связанным друг с другом. Эти координаты описываются случайными процессами, соответствующими дифференциальным уравнениям:
dg1 (t)
dt
dg2 (t)
dtdg3 (t)
dt
=−a1 (t)g1 (t) +ξ1 (t),
=−a 2 (t)g2 (t) +ξ2 (t),
=−a 3 (t)g3 (t) +ξ3 (t).
67

|
|
g |
Введем вектор |
|
1 |
|
||
g(t) = g2 |
||
|
|
|
|
|
g3 |
(t)
(t) , матрицу
(t)
|
−a (t) |
0 |
0 |
|
|
|
1 |
−a2 (t) |
0 |
|
и |
A(t) = |
0 |
|
|||
|
0 |
0 |
|
|
|
|
−a3 (t) |
|
|||
белый шум |
|
|
|
|
|
ξ1 |
(t) |
. Тогда одновекторное уравнение состояния |
||||||
|
|
|
|
|
ξ2 |
|
||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
ξ(t) = |
(t) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ3 (t) |
|
|
|
d |
|
(t) |
|
|
|
|
|
в точности описывает все заданные входные воз- |
|||||
g |
= A(t) |
|
(t) + |
|
(t) |
|||||||||
|
g |
ξ |
||||||||||||
|
|
dt |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
действия Для проверки достаточно раскрыть в этом уравнении матричные и векторные обозначения.
Пример 2. Входное воздействие с дробно-рациональным энергетическим спектром.
Пусть g(t) описывается дифференциальным уравнением ви-
да:
|
|
d 3 g(t) |
+ a1 |
d 2 g(t) |
+ a2 |
|
dg(t) |
+ a3 g(t) = ξ(t) . |
|
|||
|
|
dt 3 |
|
|
|
dt |
|
|||||
|
|
|
dt 2 |
|
|
|
|
|
||||
Найдем энергетический спектр такого воздействия. Для этого |
||||||||||||
вначале |
выполним |
|
преобразование |
Лапласа |
||||||||
p3 g( p) + a1 p2 g( p) + a2 pg( p) + a3 g( p) = ξ( p) |
|
и запишем передаточную функ- |
||||||||||
цию формирующего фильтра |
1 |
|
|
|
|
|||||||
|
|
|
Hϕ (p) = |
|
|
|
|
. |
|
|||
|
|
|
p3 + a p2 + a p + a |
|
||||||||
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
Энергетический спектр входного воздействия находится по формуле Gg (ω)= Hg ( jω)2 Nξ . При выборе различных коэффициентов a1 ,a2 ,a3 могут быть получены энергетические спектры разно-
образной формы. Но рассматриваемое уравнение имеет третий порядок. Преобразуем его в одно векторное уравнение. Введем вспо-
могательные переменные: |
d2g(t) |
= g2 (t), |
dg(t) |
= g1(t) . Тогда исходное |
||||||
dt2 |
dt |
|||||||||
|
|
|
|
|
|
|
|
|||
уравнение перепишется в форме: |
|
|
||||||||
|
dg2 (t) |
= −a1 g2 (t) − a2 g1 (t) − a3 g(t) + ξ(t) |
||||||||
|
|
|||||||||
|
dt |
|
|
|
|
|
|
|
||
|
|
(t) |
|
|
|
|
. |
|||
dg |
|
|
|
|
||||||
|
1 |
|
|
|
= g2 (t) |
|
|
|
||
dt |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
dg(t) |
= g1 (t) |
|
|
|
||||||
|
|
|
|
|
|
|||||
dt |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
68

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
(t) |
|
|
|
|
|
|
|
|
|
Введем |
|
теперь |
вектор |
|
|
|
|
|
|
2 |
|
и |
|
|
тогда |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
g(t) = g1 |
(t) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(t) |
|
|
|
|
||
|
|
|
− a1 |
− a2 |
− a3 |
|
, где |
|
|
|
ξ(t) |
|
|
− a1 |
− a2 |
− a3 |
|
. Таким |
||||||||
d g |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
dt |
|
= |
1 |
0 |
0 |
g(t) + ξ(t) |
|
ξ(t) |
= |
0 |
|
|
; A |
= |
1 |
0 |
0 |
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
|
|
|
0 |
0 |
|
|
|
|
0 |
|
|
0 |
0 |
|
||||||||||||
образом дифференциальное уравнение третьего порядка удается преобразовать к стандартной векторной форме. Очевидно, что точно так же к векторному уравнению первого порядка можно преобразовать дифференциальное уравнение произвольного порядка.
Пример 3. Полиномиальное воздействие.
Пусть g(t) = g0 +Vt + at2  2. Такой входной сигнал получается
2. Такой входной сигнал получается
как решение следующего дифференциального уравнения |
d3g |
= 0 . |
|
dt3 |
|||
|
|
Заметим, что этот результат можно рассматривать как частный слу-
чай предыдущего примера, полагая |
a = a |
|
= a |
|
= ξ ≡ 0 . |
Тогда |
d3g |
= 0 , |
||||||
|
|
|
|
|||||||||||
d 2 g = a, |
dg = at +V , g(t) =Vt + at2 |
1 |
2 |
|
|
3 |
|
|
|
|
dt3 |
|||
2 + g0 , |
|
|
a,V , g0 |
– начальные |
||||||||||
dt2 |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
условия. |
|
|
|
|
d2g(t) |
|
|
dg(t) |
|
|
||||
Введем вспомогательные переменные |
= g2 (t), |
= g1(t) . |
||||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
dt2 |
|
dt |
|||||
Тогда уравнения состояния запишутся в виде:
|
|
|
|
|
|
|
|
dg2 (t) |
= 0, |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
dg |
1 |
= g2 (t), |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
dg(t) |
= g1 (t), |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
dt |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
или в стандартной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
(t) , |
|||||||||
|
|
|
|
|
|
|
|
|
d |
g |
|
|
|
|
(t) + |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
= Ag |
ξ |
||||||||||
|
0 0 0 |
|
|
|
0 |
dt |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где A = |
1 |
0 |
0 |
, |
|
(t) = |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
69

Таким образом, исходное дифференциальное уравнение состояния ddtg = A(t)g(t) + ξ(t) описывает широкий класс реальных слу-
чайных процессов.
Пусть теперь g(t) передается по каналу связи и вместе с помехой поступает на вход системы управления:
|
|
|
|
|
|
|
|
|
|
|
z (t) |
c11 (t) ... |
c1n (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(t) = C(t) |
|
(t) + |
|
(t) , где |
|
1 |
|
, C(t)= c21 (t) ... |
c2n (t) |
|
; |
||
|
Z |
g |
n |
|||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
Z(t) = ... |
|
... ... ... |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cmn (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
zm (t) |
cm1 (t) ... |
|
|
||
|
|
|
n1 (t) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
(t) = |
... |
– помеха в виде векторного белого шума со спектраль- |
||||||||||||
n |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nm (t) |
|
|
|
|
|
|
|
|
|
|
|||
ными плотностями каждой компоненты N01(t), N02 (t),..., N0m (t) со-
ответственно.
Рассмотренная векторная модель позволяет дать математическое описание различных ситуаций, возникающих при формировании входных сигналов проектируемых САУ.
Пример 4. Предположим, что один и тот же входной сигнал g(t) передается по двум независимым каналам связи. При этом на выходе первого канала наблюдается смесь z1 (t )= c1 (t ) g (t)+ n1 (t )
сигнала g (t ) с помехой n1 (t), а на выходе второго канала наблюдается процесс z2 (t)= c2 (t) g (t)+ n2 (t ). Для того, чтобы представить такие наблюдения в стандартной векторной форме, введем векторы
|
(t )= (z1 (t ) |
z2 (t ))T , |
|
|
(t )= (n1 (t) |
|
n2 (t ))T |
и |
|
|
матрицу |
|||||||||||||
z |
n |
|
|
|
||||||||||||||||||||
c(t )= c1 |
(t) |
. В |
этом |
|
случае |
|
одно |
векторное |
|
уравнение |
||||||||||||||
|
c |
(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
(t ) |
|
|
|
|
(t ) |
|
|
|
(t ) |
|
|
||||
|
|
|
|
|
|
|
|
|
z |
c |
|
n |
|
|
||||||||||
z (t )= c(t )g (t )+ n(t ) |
или |
описыва- |
||||||||||||||||||||||
|
z |
1 |
(t ) |
|
= |
1 |
(t ) |
|
g (t )+ |
1 |
(t) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
c |
|
|
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
||||||||
ет двухканальную систему наблюдений скалярного процесса g (t).
Пример 5. Пусть входной сигнал g (t ) имеет сложный энер-
гетический спектр и описывается дифференциальным уравнением третьего порядка (см. пример 2). В этом случае уравнение состоя-
70
