
Васильев К.К. Теория автоматического управления (следяшие системы)
.pdf
m(t) = M{X (t)}, D(t) = M {X (t) − m(t))2 }.
Так же, как и для случайной величины, дисперсия характеризует разброс значений случайного процесса относительно среднего значения m(t). Чем больше D(t) , тем больше вероятность появления очень больших положительных и отрицательных значений процесса. Более удобной характеристикой является среднее квадратичное отклонение (СКО) σ(t) = D(t) , имеющее ту же размер-
ность, что и сам случайный процесс.
Если случайный процесс описывает, например, изменение дальности до объекта, то математическое ожидание – средняя дальность в метрах; дисперсия измеряется в квадратных метрах, а СКО
– в метрах и характеризует разброс возможных значений дальности относительно средней.
Среднее значение и дисперсия являются очень важными характеристиками, позволяющими судить о поведении случайного процесса в фиксированный момент времени. Однако, если необходимо оценить «скорость» изменения процесса, то наблюдений в один момент времени недостаточно. Для этого используют две случайные величины (X(t1), X(t2)), рассматриваемые совместно. Так же, как и для случайных величин, вводится характеристика связи или зависимости между X(t1)и X(t2). Для случайного процесса эта характеристика зависит от двух моментов времени t1 и t2 и называется
корреляционной функцией:
R(t1 ,t2 ) = M{(X (t1 ) − m(t1 )(X (t2 ) − m(t2 ))}.
Стационарные случайные процессы
Многие процессы в системах управления протекают однородно во времени. Их основные характеристики не изменяются. Такие процессы называются стационарными. Точное определение можно дать следующим образом. Случайный процесс X(t) называется стационарным, если любые его вероятностные характеристики не зависят от сдвига начала отсчета времени. Для стационарного случайного процесса математическое ожидание, дисперсия и СКО постоянны: m(t) = m , D(t) = D= σ 2.
41
Корреляционная функция стационарного процесса не зависит от начала отсчета t, т.е. зависит только от разности τ = t2 −t1 мо-
ментов времени:
R(τ) = M{(X(t1) − m) (X(t1 −τ) − m)}.
Корреляционная функция стационарного случайного процесса имеет следующие свойства:
1) R(τ = 0) = σ 2 ; |
2) R(τ) = R(−τ) ; |
3) R(τ →∞) = 0 . |
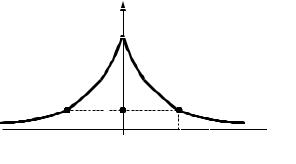
Часто корреляционные функции процессов в системах управления имеют вид, показанный на рис. 27.
R(τ) |
σ 2 |
|
σ2/е |
|
|
0 |
τk |
τ |
|
|
Рис. 27
Интервал времени τk , на котором корреляционная функция,
т.е. величина связи между значениями случайного процесса, уменьшается в М раз, называется интервалом или временем кор-
реляции случайного процесса. Обычно М=10 или М=е. Можно сказать, что значения случайного процесса, отличающиеся по времени на интервал корреляции, слабо связаны друг с другом.
Таким образом, знание корреляционной функции позволяет судить о скорости изменения случайного процесса.
Другой важной характеристикой является энергетический спектр случайного процесса. Он определяется как преобразование Фурье от корреляционной функции:
∞
G(ω) = ∫R(τ)e− jωτ dτ .
−∞
Очевидно, справедливо и обратное преобразование:
|
1 |
∞ |
|
R(τ) = |
∫G(ω)e jωτ dω . |
||
|
|||
|
2π −∞ |
||
Энергетический спектр показывает распределение мощности случайного процесса, например помехи, на оси частот.
При анализе САУ очень важно определить характеристики случайного процесса на выходе линейной системы при известных
42
характеристиках процесса на входе САУ. Предположим, что линейная система задана импульсной переходной характеристикой h(τ). Тогда выходной сигнал в момент времени t1 определяется ин-
тегралом Дюамеля:
|
|
|
∞ |
|
|
|
x(t1 )= ∫h(τ1 )g(t1 −τ1 )dτ1 , |
|
|
|
|
|
−∞ |
|
где g(t) – процесс на входе системы. Для нахождения корреляцион- |
||||
ной |
функции |
Rx (t1 ,t2 )= M{x(t1 )x(t2 )} |
запишем |
|
|
∞ |
|
|
|
x(t2 )= ∫h(t2 )g(t2 −τ2 )dτ2 |
и после перемножения найдем математи- |
|||
|
−∞ |
|
|
|
ческое ожидание |
∞ ∞ |
|
|
|
|
|
|
|
|
|
Rx (t1 , t2 ) |
= ∫ ∫h(τ1 )h(τ2 )M{g(t1 −τ1 )g(t2 −τ2 )}dτ1dτ2 . |
||
−∞ −∞
Таким образом, связь между корреляционными функциями входного и выходного случайных процессов устанавливается с помощью следующего двойного интеграла:
∞ ∞
Rx (t1 ,t2 )= ∫ ∫h(τ1 )h(τ2 )Rg (t1 −τ1 ,t2 −τ2 )dτ1dτ2 .
−∞ −∞
Для стационарных процессов корреляционные функции зависят только от разности аргументов t1 −t2 = u , (t1 −τ1 )− (t2 −τ2 )= v и
поэтому
∞ ∞
Rx (u)= ∫ ∫h(τ1 )h(τ2 )Rg (v)dτ1dτ2 .
−∞ −∞
Более простое соотношение можно найти для энергетических спектров Gg (ω) и Gx (ω) входного и выходного сигналов при из-
вестной передаточной функции W (jω) линейной системы. Дейст-
вительно, найдем преобразование Фурье от левой и правой частей последнего равенства. Получим следующее выражение:
Gx (ω)= ∞∫ ∞∫ ∞∫h(τ1 )h(τ2 )Rg (ν )e− jωudτ1dτ2du .
−∞ −∞ −∞
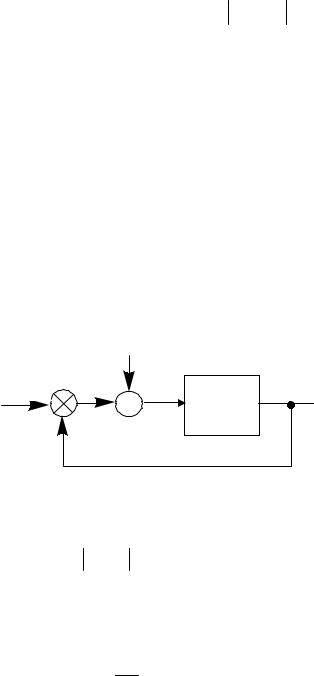
После замены переменной v = t1 −t2 − (τ1 −τ2 )= u −τ1 −τ2 или u = v +τ1 −τ2 тройной интеграл преобразуется в произведение
43
|
|
жҐ |
|
|
- jwt |
1 |
|
|
цжҐ |
|
jwt |
2 |
|
|
цжҐ |
|
|
ц |
|||
|
|
з |
|
|
|
|
|
|
з |
|
|
|
|
|
з |
|
|
- jwv |
ч |
||
G |
w |
= з |
т |
h t e |
|
dt |
|
ч |
т |
h t e |
|
|
dt |
|
ч |
т |
|
||||
|
1 |
чз |
|
|
2 |
чз |
R v e |
dvч. |
|||||||||||||
|
x ( ) |
з |
( |
1 ) |
|
|
|
чз |
( 2 ) |
|
|
|
чз |
g ( ) |
|
ч |
|||||
|
|
з |
|
|
|
|
|
|
|
чз |
|
|
|
|
|
|
чз |
|
|
|
ч |
|
|
и- Ґ |
|
|
|
|
|
|
ши- Ґ |
|
|
|
|
|
ши- Ґ |
|
|
ш |
|||
Поскольку преобразование Фурье от импульсной характеристики дает передаточную функцию, находим окончательно связь между энергетическими спектрами процессов на входе и на выходе линейной системы:
Gx (ω)=W (jω)W (− jω)Gg (ω) = W (jω)2 Gg (ω) .
Часто помехи в системах управления имеют очень широкий спектр. В таких случаях их удобно представить в виде так называемого белого шума – процесса с постоянным энергетическим спектром: G(ω) = No. Корреляционная функция белого шума R(τ) = N0δ(τ) , где δ(t) – импульсная дельта-функция. Это означает,
что даже очень близкие по времени значения белого шума не связаны друг с другом.
Воздействие помех на системы управления
Рассмотрим воздействие помехи n(t) на замкнутую линейную систему управления (рис. 28). Будем предполагать, что нам известен энергетический спектр Gn (ω) помехи.
g(t) |
+ |
|
n(t) |
X(t) |
|
+ |
H(p) |
||||
|
- |
|
|||
|
|
|
|
Рис. 28 Найдем дисперсию ошибки, возникающей при действии по-
мехи n(t). Для этого вначале определим энергетический спектр на
выходе системы Gвых(ω) = W ( p) 2 Gn (ω) , где W(p) = H(p) / (1+H(p)) –
передаточная функция замкнутой системы управления. После этого с помощью обратного преобразования Фурье можно найти корреляционную функцию помехи на выходе системы:
Rвых(τ) = 21π ∞∫Gвых(ω)e jωτ dω .
−∞
44

Наконец, учитывая, что дисперсия σвых2 = Rвых(0) , получаем оконча-
тельное выражение для дисперсии ошибки системы управления:
σ 2 = 21π ∞∫Gвых(ω)dω.
−∞
Пример. Пусть на входе системы, содержащей один интегратор, например, в системе управления приводом, действует широкополосная помеха с энергетическим спектром G n (ω) = N o. Переда-
точная функция системы с одним интегратором H(p) = |
k |
. Опреде- |
|
p |
|||
|
|
лим дисперсию ошибки, вызванной действием помехи. Для этого вначале запишем выражение для передаточной функции замкнутой
системы |
W ( p) = |
|
|
|
H ( p) |
|
= |
|
k |
|
|
|
и |
найдем |
|
квадрат ее модуля: |
|||||||||||||||||||
1 + H ( p) |
p |
+ k |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
W ( p) |
|
2 = |
|
|
. |
|
Энергетический спектр помехи на выходе рас- |
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
ω2 + k 2 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сматриваемой системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
G |
(ω) = |
|
W ( p) |
|
2 |
G |
(ω) = |
|
|
N |
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
вых |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
ω2 + k2 |
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Таким образом, дисперсия ошибки САУ, вызванной действием |
|||||||||||||||||||||||||||||||||
помехи, находится по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
1 ∞ |
|
k 2 N0 |
|
|
|
|
|
|
|
kN0 |
|
∞ |
dz |
|
|
1 |
|
|||||||
|
|
|
|
|
σвых |
= |
|
|
−∞∫ |
|
|
|
dω = |
|
−∞∫ |
|
|
= |
|
kN0 . |
|||||||||||||||
|
|
|
|
|
|
2π |
ω2 |
|
+ k 2 |
2π |
z 2 |
+1 |
2 |
||||||||||||||||||||||
Описание траекторий движения объектов с помощью случайных процессов
Входные сигналы САУ часто могут быть представлены с помощью типовых детерминированных воздействий. Например, движение объекта с известной постоянной скоростью определяется уравнением g (t)= g0 + vt . Однако изменение входных сигналов во
времени не всегда может быть задано с помощью известных детерминированных функций. Во многих случаях для более реалистичного описания, например, траектории движения самолета или корабля, необходимо использовать случайные процессы. При этом известная детерминированная составляющая входного сигнала мо-
45

жет рассматриваться как математическое ожидание m(t) случайного процесса:
g(t)= m(t)+g0 (t),
где g0 (t) – стационарный случайный процесс с нулевым математическим ожиданием и корреляционной функцией
Таким образом, второе слагаемое g0 (t) описывает неизвест-
ный нам до эксперимента входной сигнал САУ в виде реализаций случайного процесса. Корреляционная функция этого случайного процесса позволяет задать дисперсию σg2 = R g (τ = 0) и «среднюю
скорость» изменения входного сигнала, связанную с интервалом корреляции процесса g0 (t). На практике приближенные значения
m(t) и R g (τ) можно получить экспериментально, если в распоряже-
нии разработчика |
системы |
имеется большое число N записей |
g(k) (t), k =1,2,..., N , |
реальных |
входных сигналов. Математическое |
ожидание в этом случае оценивается средним арифметическим
m* (t)= 1 ∑N g(k) (t),
N k=1
а для оценки корреляционной функции используется следующая формула:
(k) (t)g(k) (t +τ).
Процесс g0 (t) можно считать стационарным, если результаты расчетов по этой формуле мало зависят от выбора начала отсчета вре-
мени t. |
|
|
|
Пусть входной сигнал |
САУ задан в |
виде |
суммы |
g(t)= m(t)+g0 (t). Для нахождения |
динамических |
ошибок, |
возни- |
кающих в линейной системе управления, можно воспользоваться принципом суперпозиции. Величина установившейся динамической ошибки за счет детерминированной составляющей изменения входного сигнала находится по известной формуле:
εуст = lim pε(p), |
||||
|
p→0 |
|
||
где ε(p)= Hε (p)m(p); Hε (p)= |
1 |
|
– передаточная функция по |
|
1+ H(p) |
||||
ошибке; m(p) – изображение |
|
|||
m(t) по Лапласу. |
||||
46

Случайная составляющая характеризуется величиной дисперсии динамической ошибки:
σε2 = Rε (τ = 0).
Для нахождения корреляционной функции Rε (τ) случайной состав-
ляющей динамической ошибки вначале находят энергетический спектр Gg (ω) процесса g0 (t) как преобразование Фурье R g (τ). После
этого легко находятся энергетический спектр
Gε (ω)= Hε (jω)2 Gg (ω)
и корреляционная функция динамической ошибки
Rε (τ)= 21π −∞∫∞Gε (ω)e jωτ dω .
Суммарное воздействие детерминированного m(t) и случайного g0 (t) входного сигнала g(t) может быть оценено средним квадратом динамической ошибки
|
M{(g(t)− x(t))2 }= εуст2 +σε2 . |
Пример 1. Предположим, что на САУ (рис. 28) с одним инте- |
|
гратором (H(p)= k / p ) |
поступает входной сигнал g(t)= vt +g0 (t), где |
g0 (t) – случайный |
процесс с корреляционной функцией |
R g (τ)=σg2e−a τ . Определим в отсутствие помех (n(t)≡ 0 ) средний
квадрат динамической ошибки такой системы управления. Вначале найдем установившуюся ошибку за счет детермини-
рованного слагаемого m(t)= vt входного воздействия. Для системы с астатизмом первого порядка εуст = v / k . Энергетический спектр
Gg (ω) случайной составляющей g0 (t) входного воздействия находится как преобразование Фурье корреляционной функции:
Gg (ω)= ∞∫ Rg (τ )e− jωτ dτ = |
2aσg2 |
|
. |
2 |
2 |
||
−∞ |
ω + a |
|
|
Заметим, что Tk =1/ a является интервалом корреляции случайного процесса g0 (t) на уровне 1/ e . С другой стороны, параметр a равен ширине энергетического спектра случайного процесса g0 (t) на уровне 0.5, т.е. Gg (ω = a)/ Gg (ω = 0)= 0.5 .
После нахождения энергетического спектра случайной составляющей динамической ошибки
47

Gε (ω)= |
|
Hε (jω) |
|
2 Gg (ω)= |
|
1 |
|
|
|
|
|||||
|
|
1 |
+ H(jω) |
||||
|
|
|
|
|
|||
2 Gg (ω)= (ω2ω+2k2 )(ω2 +a 2 )
находим дисперсию динамической ошибки
σε2 = Rε (0)= 21π −∞∫∞Gε (ω)dω = a + k .
Средний квадрат динамической ошибки с учетом детерминированной и случайной составляющих определяется как сумма
2 |
2 |
|
v2 |
|
aσg2 |
. |
|
εуст +σε |
= |
|
+ |
|
|||
k2 |
a +k |
||||||
|
|
|
|
|
|||
Из полученного выражения следует, что при заданных параметрах a, v, σg2 входного сигнала уменьшение динамической ошибки
достигается при увеличении коэффициента k усиления звена САУ.
Оптимизация параметров системы управления
Динамические ошибки при описании входного сигнала детерминированными функциями g(p) в установившемся режиме оп-
ределяются по формуле:
εуст = lim Hε (p)g(p),
p→0
где Hε (p)= |
|
|
1 |
|
;H(p) - передаточная функция разомкнутой САУ. |
|
1 |
+ H(p) |
|||||
|
|
|||||
При описании входного сигнала реализациями случайного процесса g0 (t) динамические ошибки характеризуются величиной дисперсии
σε2 = 21π −∞∫∞Hε (jω)2 Gg (ω)dω ,
где Gg (ω) - энергетический спектр входного сигнала g0 (t). При наличии детерминированных m(t) и случайных g0 (t) составляющих входного сигнала g(t)= m(t)+g0 (t) величину динамических ошибок целесообразно оценивать средним квадратом суммарной ошибки
εуст2 +σε2 .
Кроме динамических, в САУ имеются ошибки, вызванные действием помех n(t). Влияние помех можно характеризовать
48

дисперсией σвых2 выходного сигнала САУ
σвых2 = 21π ∞∫ Wn (jω)2 Gn (ω)dω ,
−∞
где Wn (jω) - передаточная функция по помехе; Gn (ω) - энергетиче-
ский спектр помехи. Как правило, помехи в САУ могут быть представлены белым шумом с постоянным на всех частотах энергетическим спектром Gn (ω)= N0 . Кроме того, помехи часто действуют на
вход системы и тогда передаточная функция по помехе Wn (jω) совпадает с передаточной функцией W(jω)= 1+H(jω) замкнутой САУ.
Во всех современных САУ присутствуют как динамические ошибки, так и ошибки за счет действия помех. Для характеристики качества системы управления при наличии динамических и случайных ошибок используют средний квадрат суммарной ошибки:
εс2 =εуст2 +σε2 +σвых2 ,
который зависит от параметров a = (a1 , a2 ,..., am )T системы. Парамет-
ры a обычно выбираются таким образом, чтобы обеспечить условие минимума квадрата суммарной ошибки main ε2С . В этом случае
говорят об оптимизации параметров системы управления по критерию минимума квадрата суммарной ошибки.
Пример 2. Рассмотрим систему привода антенны или рулей летательного аппарата (см. п. 1.1), находящуюся под воздействием помех (рис. 29).
x(t) n(t)


 + g(t)
+ g(t)
Ку
u(t)
Рис. 29
В такой системе угол поворота х(t) вала двигателя должен повторять заданную траекторию движения – входной сигнал g(t).
49

Помеха n(t) в данном случае описывает погрешности измерения
х(t).
Упрощенная эквивалентная схема такой системы представ-
лена на рис. 30, где |
H( p) = |
k |
, k=ку кдв – коэффициент пере- |
p(1+ pT) |
дачи системы; Т – постоянная времени двигателя.
g(t) |
n(t) |
x(t) |
||
+ |
||||
+ |
|
H(p) |
||
– |
|
|
||
Рис. 30 Предположим, что заданная траектория движения описыва-
ется линейной функцией g(t)=Vt. Тогда установившиеся динамические ошибки системы с одним интегратором определяются по формуле εуст =V / k . Чем выше коэффициент усиления k , тем меньше
величина динамической ошибки в установившемся режиме. Будем аппроксимировать помеху белым шумом со спек-
тральной плотностью Gn(ω)=N0. Тогда Gвых(ω)= |
|
|
H( jω) |
|
|
2 |
|||
|
|
|
|||||||
|
|
|
|
|
N0 и |
||||
1 |
+ H( jω) |
||||||||
|
|
|
|
|
|
||||
после преобразований находим: σ2ε = |
N0K |
. Из этой формулы следу- |
|||||||
2 |
|||||||||
|
|
|
|
|
|
|
|
||
ет, что для уменьшения влияния помех необходимо снижать коэффициент усиления k, т.е. повышать инерционность системы управления.
Квадрат суммарной ошибки определяется следующим выра-
жением: |
εc2 =εуст2 +σвых2 = V 2 |
+ |
N0k |
. На основе этой формулы можно |
|
2 |
|||||
|
k2 |
|
= εС2 (k) (рис. 31). |
||
построить график зависимости εС2 |
|||||
εc2 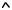
0 |
k0 |
k |
Рис. 31
50
