Доведення

Необхідність. Нехай диференційовна в точці . Тоді . З означення похідної будемо мати:

, , коли . (2)

, , , де і , коли , .

Підставимо все це в (2) і виділивши дійсні і уявні частини та зрівнявши їх, одержимо

( )

( )

, коли , . Останні дві рівності, врахувавши як ведуть себе та , а також що числа і незалежні від та , означають як ми знаємо з дійсного аналізу, що функції і як функції двох дійсних змінних диференційовні в точці . Перша частина необхідності доведена.

З рівності ( ) будемо мати

,

З рівності ( ) випливає

, .

З останніх 4-ох рівностей і одержуємо умови Коші-Рімана (1). Необхідність доведена, причому ми ще й отримали

.

Достатність. Нехай умови (1) виконуються. Покажемо, що похідна функції існує. З умови (1) матимемо, що

, , коли , (3)

, , коли , . (4)

Покладемо та . Підставивши в (3) і (4) замість відповідних часткових похідних та і помноживши (4) на та додавши її до (3) одержимо:

.

З цієї рівності будемо мати:

.

Оскільки останні два доданки справа прямують до 0, коли (бо при цьому , ), , то з останньої рівності маємо, що існує .

Теорема доведена.

Приклад. Перевіримо на диференційованість функцію

, .

1) функції і диференційовані на всій площині як функції двох дійсних змінних;

2) Перевіримо умови Коші-Рімана

, ,

, , .

Ці умови виконуються, а отже за критерієм диференційованості дана функція є диференційованою на всій комплексній площині.

§2 Геометричний зміст аргументу і модуля похідної

Простий аналіз показує, що якщо ми маємо комплексно-значну функцію , де , то ця функція зображатиме на площині неперервну криву, якщо тільки , неперервні на відрізку функції. Нехай далі неперервна на відрізку функція, причому існує . З’ясуємо що це геометрично буде означати.

Візьмемо довільну точку і відмітимо на нашій кривій точку . Початок кривої точка . Проведемо січну . Очевидно, що кут, який утворює ця січна з додатнім напрямом осі буде співпадати з аргументом комплексного числа . Далі зрозуміло, що існування граничного положення цієї січної при прямуванні точки до точки по кривій, а воно буде дотичною до кривої в точці буде залежати від того існує чи ні . Оскільки аргумент числа 0 невизначений, то переконаємося, що при всіх достатньо близьких до . 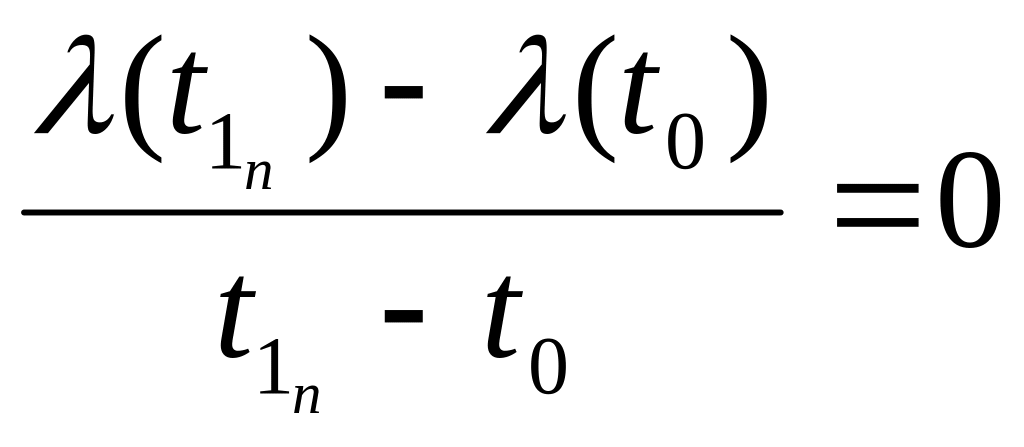Справді, якби це було не так, то знайшлася б послідовність : і , а тоді ми мали б, що і оскільки і в точці існує похідна , то вона дорівнювала б 0, а в нас це не так. Отже, при всіх достатньо близьких до дріб під знаком аргументу відмінний від 0 і цей вираз має зміст при . Оскільки існує , то існує . Звідси одержимо, що . Таким чином ми встановили:

Наявність відмінної від 0 похідної від комплексно-значної функції дійсного аргументу в деякій точці означає існування у відповідній точці цієї кривої дотичної, кут нахилу якої до додатного напряму осі дорівнює .

Нехай тепер ми знову ж в комплексній площині маємо таку саму неперервну криву , причому і далі в деякій області, що містить цю криву, задана неперервна функція (комплексно значна комплексного аргументу), причому в точці існує . Тоді ця функція переведе нашу неперервну криву в -площині в деяку також неперервну (бо функція неперервна на ) криву в -площині, яка пройде через точку . Покажемо, що функція (комплексно значна дійсного аргументу ) має похідну в точці . Справді, це є складна функція така, що диференційовна в точці , а диференційована в точці . Тоді за теоремою про похідну складеної функції (вона, як ми відмітили, теж переноситься на комплексну площину) матимемо, що . Отже, існування відмінної від нуля похідної цієї функції означає (див. попередній висновок) наявність до кривої дотичної в точці . Причому з того ж висновку маємо, що кут її нахилу до додатного напряму осі дорівнює аргументу цієї похідної, тобто . Одержана рівність показує, що дотична до кривої в точці при нашому відображенні повернулася на кут . Зауважимо, що величина цього кута не залежить від кривої . А раз так, то «випустивши» з точки дві такі криві, ми зразу одержимо, що при відображенні , для якого існує , криві в -площині, які є образами тільки що описаних кривих, при цьому відображенні утворять в точці той самий кут, що і криві в - площині (бо обидві дотичні до кривих і повернуться при відображенні на один і той же кут ).

Відображення, які не змінюють кутів між кривими ( ні по величині ні по напрямку) називаються конформними.

Підсумуємо все зроблене вище у вигляді такого твердження:

відображення, що здійснюється неперервною в області функцією, яка в деякій точці має відмінну від 0 похідну, є конформними в цій точці;

якщо ж функція має похідну в кожній точці області, яка до того ж там відмінна від 0, то відображення, що здійснюється такою функцією, буде конформним на всій області.

В цьому полягає геометричний зміст аргументу похідної.

Розберемося тепер з геометричним змістом модуля похідної. З означення похідної маємо:

.

Простий аналіз останньої рівності показує, що означає в скільки разів збільшуються довжини векторів , які виходять з точки , коли точки близькі до точки , при відображенні їх функцією . Інакше кажучи, − це коефіцієнт розтягу або стиску комплексної площини при відображенні в точці .

Зауважимо, повертаючись до конформних відображень, що умова для конформності відображення в точці є суттєвою. Є функції, для яких похідна в цій точці дорівнює 0 , але кути між кривими, що виходять з цієї точки змінюються. Прикладом останньої є функція в точці .

Приклад. Перевіримо яка частина простору

стискується при відображенні , а яка розтягується і яка залишається незмінною.

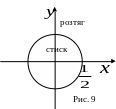
− область розтягу,

− область стиску,

− незмінна область. (Див. рис. 9).

Проілюструємо все вище сказане на прикладі дробово-лінійної функції.