
- •1 Основные понятия
- •2.2.2 Проверка гипотезы о значении генеральной средней при неизвестной дисперсии
- •2.2.3 Проверка гипотезы о значении дисперсии генеральной совокупности
- •2.2.6 Проверка гипотезы относительно доли признака (о вероятности "р" биномиального распределения)
- •2.3 Критерии согласия
- •2.3.1 Критерий согласия х2 Пирсона
- •2.3.2 Критерий Колмогорова-Смирнова
- •2.3.3 Критерий w2 (критерий Мизеса)
2.2.6 Проверка гипотезы относительно доли признака (о вероятности "р" биномиального распределения)
Пусть имеется
выборка объемом "n",
в которой некоторый признак генеральной
совокупности наблюдается "m"-раз.
Требуется проверить гипотезу Н0
о том, что доля "р" признака в
генеральной совокупности равна некоторой
нормативной величине "р0"
(то есть Н0: р=р0),
против альтернативной гипотезы Н1:
р=р1 или Н1:![]() .
.
Для проверки
гипотезы рассмотрим случайную величину
![]() ,
являющуюся выборочной оценкой вероятности
р проявления некоторого признака
генеральной совокупности в одном
наблюдении из серии "n"
независимых наблюдений. Очевидно, что
р* распределена биномиально
и при этом
,
являющуюся выборочной оценкой вероятности
р проявления некоторого признака
генеральной совокупности в одном
наблюдении из серии "n"
независимых наблюдений. Очевидно, что
р* распределена биномиально
и при этом
![]() ,
,
![]() .
.
При достаточно большом "n" и при условии выполнения нулевой гипотезы статистика
![]()
может считаться
распределенной асимптотически нормально
с параметрами
![]() ;
;
![]() .
.
Пусть Н1:
![]() и
и
![]() .
Построим правостороннюю критическую
область:
.
Построим правостороннюю критическую
область:
,
![]() ,
,
![]() .
.
и, если
![]() ,
то Н0 отвергается, иначе Н0
принимаем.
,
то Н0 отвергается, иначе Н0
принимаем.
Пусть Н1:
и
![]() .
Построим левостороннюю критическую
область:
.
Построим левостороннюю критическую
область:
,
![]() ,
,
![]()
если , то Н0 отвергаем, иначе Н0 не противоречит выборочным данным.
Пусть Н1:
![]() .
Построим двустороннюю критическую
область:
.
Построим двустороннюю критическую
область:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
если
![]() ,
то гипотеза Н0 принимается, иначе
отвергается.
,
то гипотеза Н0 принимается, иначе
отвергается.
2.3 Критерии согласия
Для статистической
проверки гипотез о теоретическом
(модельном) виде закона распределения
вероятностей исследуемой случайной
величины
![]() используют критерии согласия. На
основании оценки закона распределения
в форме ряда распределения, статистической
функции распределения, полигона,
гистограммы или иных соображений, порой
априорного характера, мы делаем
предположение о модельном виде закона
распределения (выдвигаем нулевую
гипотезу) Н0:
используют критерии согласия. На
основании оценки закона распределения
в форме ряда распределения, статистической
функции распределения, полигона,
гистограммы или иных соображений, порой
априорного характера, мы делаем
предположение о модельном виде закона
распределения (выдвигаем нулевую
гипотезу) Н0:
![]() ,
где
,
где
![]() - вектор параметров теоретического
распределения. К примеру, Н0:
случайная величина (генеральная
совокупность) распределена биномиально
или равномерно, или нормально и т.п. При
этом возможна, как ситуация, когда вектор
параметров
гипотетического распределения неизвестен,
так и ситуация когда вектор
известен. Наша задача на основании "n"
независимых наблюдений (выборки)
случайной величины
проверить справедливость гипотезы Н0
или отвергнуть ее. Для проверки гипотезы
выбираются (строятся) критические
статистики, измеряющие расстояние между
эмпирическим законом распределения
- вектор параметров теоретического
распределения. К примеру, Н0:
случайная величина (генеральная
совокупность) распределена биномиально
или равномерно, или нормально и т.п. При
этом возможна, как ситуация, когда вектор
параметров
гипотетического распределения неизвестен,
так и ситуация когда вектор
известен. Наша задача на основании "n"
независимых наблюдений (выборки)
случайной величины
проверить справедливость гипотезы Н0
или отвергнуть ее. Для проверки гипотезы
выбираются (строятся) критические
статистики, измеряющие расстояние между
эмпирическим законом распределения
![]() и гипотетическим семейством
и гипотетическим семейством
![]() .
Заметим, что если
неизвестен, то предварительно ищут его
состоятельную и, по возможности,
эффективную оценку.
.
Заметим, что если
неизвестен, то предварительно ищут его
состоятельную и, по возможности,
эффективную оценку.
2.3.1 Критерий согласия х2 Пирсона
Этот критерий позволяет проверить гипотезы о виде распределения, как для дискретных, так и непрерывных величин. Критерий основан на теореме Пирсона-Фишера согласно которой, если гипотеза Н0 о характере распределения справедлива, то критическая статистика
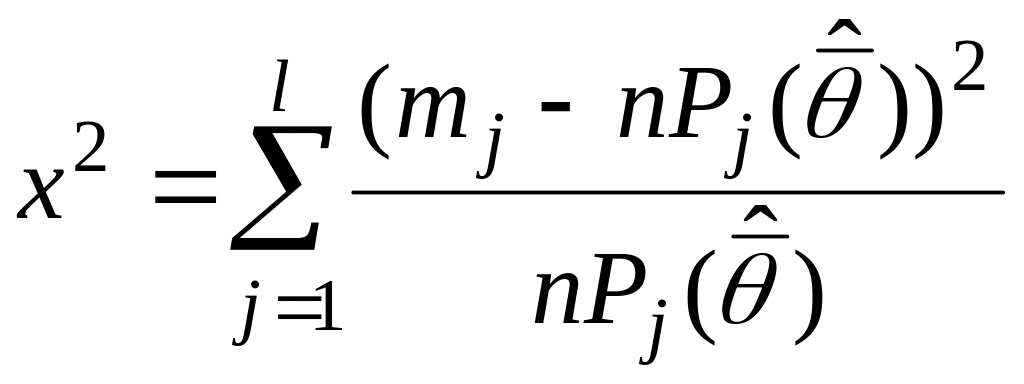 (2.6)
(2.6)
имеет (при
![]() )
распределение хи-квадрат с
)
распределение хи-квадрат с
![]() степенями свободы, где l
– число возможных вариант дискретного
вариационного ряда или число интервалов
интервального вариационного ряда; mj
– частота варианты xj
дискретного вариационного ряда или
частота попадания наблюденных значений
в j-ый интервал
интервального вариационного ряда; n
– объем выборки;
степенями свободы, где l
– число возможных вариант дискретного
вариационного ряда или число интервалов
интервального вариационного ряда; mj
– частота варианты xj
дискретного вариационного ряда или
частота попадания наблюденных значений
в j-ый интервал
интервального вариационного ряда; n
– объем выборки;
![]() - выборочная, несмещенная, состоятельная
оценка вектора параметров
гипотетического распределения (если
он неизвестен);
- выборочная, несмещенная, состоятельная
оценка вектора параметров
гипотетического распределения (если
он неизвестен);
![]() - вероятность наблюдения варианты xj
или вероятность попадания исследуемой
случайной величины в j-ый
интервал, вычисленная с помощью
гипотетического распределения
- вероятность наблюдения варианты xj
или вероятность попадания исследуемой
случайной величины в j-ый
интервал, вычисленная с помощью
гипотетического распределения
![]() ,
в котором
(если он неизвестен) заменен на
;
n – объем выборки; к –
число параметров предполагаемого
теоретического распределения оцениваемых
по выборке, то есть, если
- известен, то к=0, а если
- неизвестен, то к – размерность
;
,
в котором
(если он неизвестен) заменен на
;
n – объем выборки; к –
число параметров предполагаемого
теоретического распределения оцениваемых
по выборке, то есть, если
- известен, то к=0, а если
- неизвестен, то к – размерность
;
![]() - называют теоретической частотой.
- называют теоретической частотой.
Р.S.
Заметим, что не рекомендуется исходить
из слишком малых
![]() ,
а поэтому при расчете целесообразно
объединить интервалы так, чтобы
,
а поэтому при расчете целесообразно
объединить интервалы так, чтобы
![]() для объединенных интервалов. Объем
выборки должен быть достаточно велик:
для объединенных интервалов. Объем
выборки должен быть достаточно велик:
![]() .
.
Для проверки
гипотезы Н0:
![]() строим двустороннюю критическую область
строим двустороннюю критическую область
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
Гипотеза Н0 не отклоняется, если:
![]() ,
в противном случае гипотезу Н0
следует отклонить. При этом обратим
внимание на то, что гипотеза Н0
отклоняется, как при слишком больших
отклонениях теоретического распределения
от эмпирического, так и при слишком
малых, поскольку такие ситуации следует
считать маловероятными (неправдоподобными).
,
в противном случае гипотезу Н0
следует отклонить. При этом обратим
внимание на то, что гипотеза Н0
отклоняется, как при слишком больших
отклонениях теоретического распределения
от эмпирического, так и при слишком
малых, поскольку такие ситуации следует
считать маловероятными (неправдоподобными).
