25

6. Выбросы случайных процессов

6.1. Общие понятия

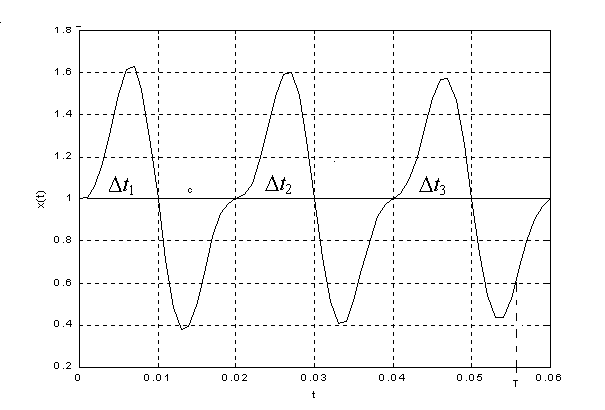Рассмотрим некоторую реализацию случайного процесса X(t) в течение конечного интервала времени Т. Если задать фиксированный уровень с, то в интервале 0…Т эта реализация может несколько раз превышать уровень с (рис.6.1).

Рис.6.1. Выбросы реализации случайного процесса за уровень с

Будем называть пересечение процессом X(t) заданного уровня с положительной производной (снизу вверх) положительным выбросом, сверху вниз – отрицательным выбросом. Ограничиваясь положительными выбросами, поставим перед собой задачу определить их следующие вероятностные характеристики:

• числовые характеристики случайного числа выбросов за интервал времени Т;

• числовые характеристики случайного времени в интервале Т, в течение которого процесс X(t) превышает заданный уровень с.

6.2. Математическое ожидание числа положительных выбросов

Для того, чтобы в интервале t…t+t произошел бы положительный выброс, необходимо выполнение следующих неравенств:

 с,  с.

Эти неравенства при их объединении запишутся в виде:

 X(t) c. (6.1)

Поэтому вероятность положительного выброса в интервале определится как вероятность следующего события:

 X(t) c) при  (6.2)

Введем условную плотность распределения вероятностей процесса X(t) при фиксированном значении производной в этот момент времени . При этом условная вероятность выброса определится как

. (6.3)

Безусловная вероятность выброса в момент времени t ,будет:

(6.4)

В (6.4) принято следующее обозначение:

временная плотность распределения вероятности выброса за уровень с в момент времени t.

Для определения математического ожидания числа выбросов за уровень с в интервале времени T (t₀, t₀+T), разобьем этот интервал на n малых интервалов (t_j, t_j+t_j) и введем случайные величины Z_j, равные 1, если в этом интервале произошел выброс, и равные 0, если выброса не было. Тогда полное число выбросов за время Т будет . Математическое ожидание числа выбросов определится как:

, (6.5)

где . (6.6)

Подставляя (6.6) в (6.5), будем иметь:

. (6.7)

При

. (6.8)

Если процесс стационарен и плотность не зависит от времени, то

. (6.9)

В случае нормального стационарного процесса X(t) процесс , линейно связанный с X(t), также нормален. При этом m_Y=0. Покажем, что процессы X(t) и Y(t) в совпадающие моменты времени некоррелированы. Действительно, обращаясь к аппарату спектральных плотностей, запишем:

. (6.10)

В соответствии с обратным преобразованием Лапласа

. (6.11)

При  , (6.12)

В случае стационарного нормального процесса плотность распределения системы X и Y, входящая в выражение (6.9), не зависит от сечения процесса во времени:

. (6.13)

Подставляя (6.13) в (6.8), получим:

(6.14)

В случае центрированной случайной величины Y интеграл, входящий в (6.14), является дисперсией этой случайной величины. Поэтому математическое ожидание числа превышения нормальным стационарным процессом уровня с определится как

. (6.15)

Следует отметить, что при определении вероятностных характеристик необходимо, чтобы существовала вторая непрерывная производная корреляционной функции при . Действительно . Так например, нельзя аппроксимировать выражением . В этом случае

т.е. первая производная корреляционной функции при  терпит разрыв, следовательно вторая непрерывная производная в этот момент времени не существует.

Пример. Корреляционная функция нормального стационарного процесса X(t) аппроксимируется выражением ). Первая и вторая производные этой корреляционной функции при  будут:

, .

Следовательно,

(6.16)

Искомое математическое ожидание числа выбросов за время Т при этом определится как

. (6.17)

Пусть напряжение на шинах узла электрической сети представляет собой стационарный нормальный случайный процесс с математическим ожиданием равным номинальному напряжению, принимаемому в относительных единицах равным m_X =1. Среднее квадратическое отклонение напряжения в относительных единицах  _X=0.1. Параметр  корреляционной функции равен =1 1/час. Определить математические ожидания числа превышений номинального напряжения выше уровня с=var в течение суток (Т=24 часа):

.

6.3. Математическое ожидание времени превышения процессом X(t)

заданного уровня

Время превышения процессом X(t) в течение интервала Т уровня с согласно рис.6.1. может быть представлено как . Математическое ожидание этого времени определится как:

. (6.18)

При (

. (6.19)

В случае стационарного процесса

. (6.20)

И наконец в случае нормального стационарного процесса:

, (6.21)

где  интеграл вероятности или функция Лапласа.

Из (6.19)…(6.21) следует, что математическое ожидание времени превышения случайным процессом некоторого заданного уровня не зависит от вида аппроксимации его корреляционной функции.

Пример. В условиях предыдущего примера определим по (6.21) математические ожидания времени превышения номинального напряжения в некотором узле электрической сети над различными заданными уровнями в течение суток (время приводится в часах):