1.3.5 Принцип формирования общей матрицы жесткости конструкции.

Полученная система уравнений является канонической системой метода перемещений, следовательно, каждый ее компонент K_i,j является реакцией в i-ой связи на единичное смещений j-ой связи. Реакция в i-ой связи складывается из реакций, возникающих во всех примыкающих к ней элементов в направлении i.

Поэтому матрица жесткости всей системы K получается путем сложения матриц жесткости всех элементов K_Э, составляющих систему:

Получающаяся в результате матрица K – квадратная, симметричная относительно главной диагонали.

Главный принцип заполнения – соответствие локальных и глобальных степеней свободы. Составим глобальную матрицу жесткости для рассмотренной выше фермы. Вычислим локальные матрицы жесткости для каждого элемента.

Элемент 1 (sin  = 0.8; cos  = 0.6).

Элемент 2 (sin  = 0.8; cos  = -0.6).

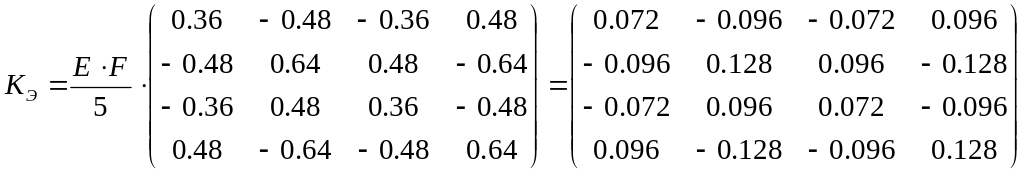
Элемент 3 (sin  = 0; cos  = 1.0).

Элемент 4 (sin  = -0.8; cos  = 0.6).

Элемент 5 (sin  = 0.8; cos  = 0.6).

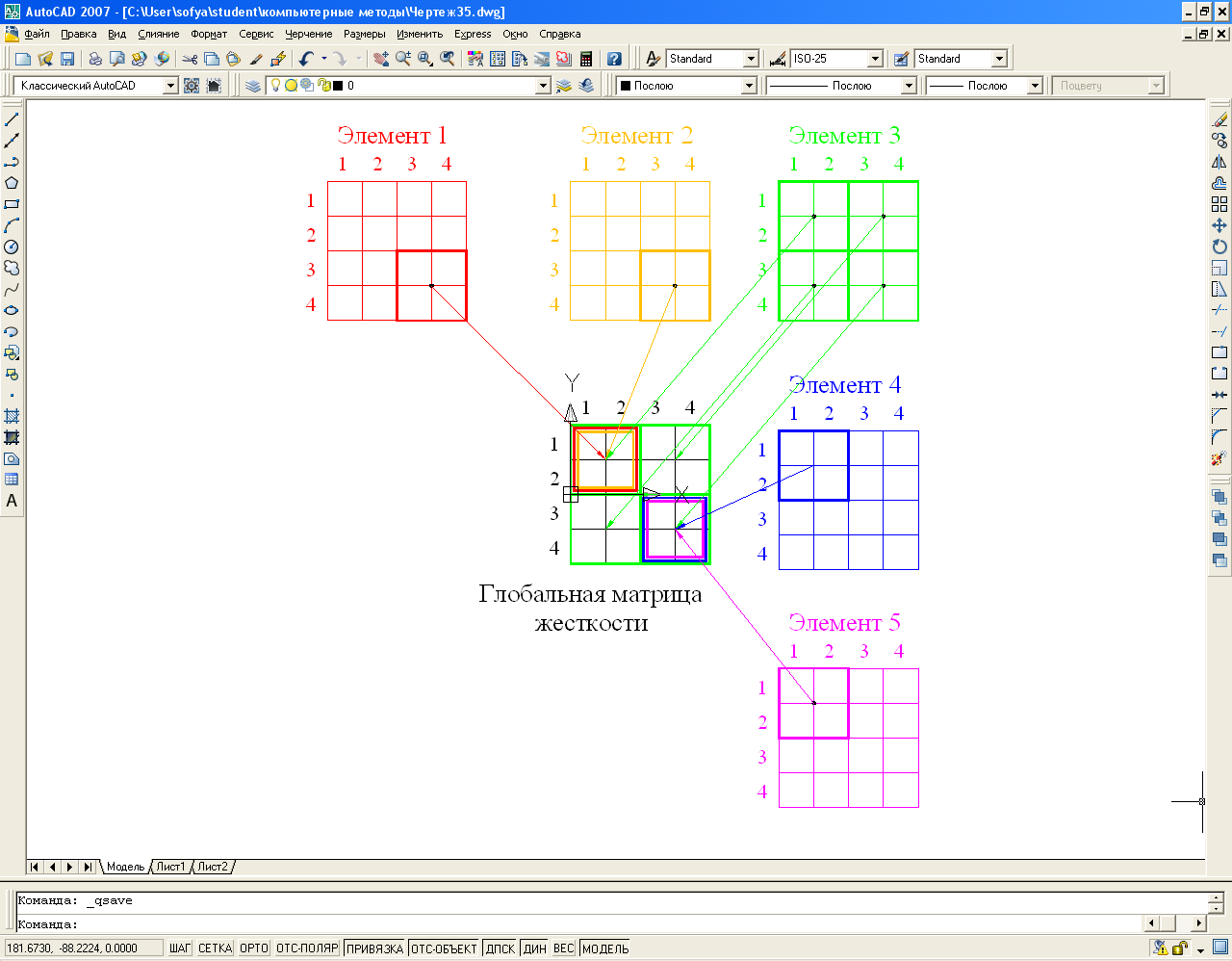
Рис. 13. Порядок суммирования матриц жесткости.

Берем элемент 1. Начальный узел элемента закреплен, следовательно коэффициенты, соответствующие первым двум локальным степеням свободы (первые две строки и столбца) не используются. Локальные степени свободы 3 и 4 соответствуют глобальным степеням свободы 1 и 2. Поэтому часть локальной матрицы 3-4 помещается на пересечение 1-2 строк и столбцов глобальной матрицы K, как показано на рисунке 13.

Аналогично для элемента 2 локальные степени свободы 3-4 соответствуют глобальным степеням свободы 1 и 2. Следовательно содержимое ячеек 3-4 складываются с величинами, уже помещенными в ячейки 1-2 глобальной матрицы от элемента 1.

Для элемента 3 локальные степени свободы 1 и 2 соответствуют глобальным степеням свободы 1 и 2, а локальные степени свободы 3 и 4 соответствуют глобальным степеням 3 и 4. Матрица жесткости этого элемента вставляется в глобальную матрицу жесткости, как показано на рисунке 13. Ее содержимое суммируется с теми ячейками, которые уже заполнены.

Процедура вложения для элементов 4 и 5 аналогична элементам 1 и 2 (но вкладываются в глобальную матрицу ячейки 1-2 локальной матрицы).

В результате глобальная матрица K выглядит следующим образом:

		-0.25	0
		0	0
-0.25	0
0	0

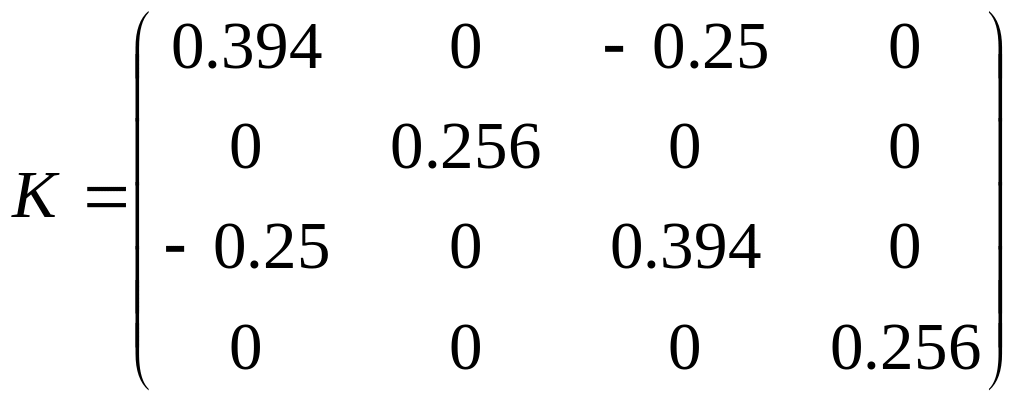
Что соответствует матрице жесткости, полученной при помощи ММП.

1.3.6 Определение перемещений и усилий в элементах.

После формирования матрицы жесткости решается система уравнений , и находится вектор перемещений Z. Усилия в конструкции находятся для каждого элемента в отдельности по формуле:

При этом из глобального вектора Z выбираются те члены, которые соответствуют нужным в данной операции локальным степеням свободы.

Если были заданы какие-либо внеузловые воздействия на элемента, то грузовые эпюры добавляются к расчетным:

S = S + S₀

1.4 Основные расчеты, выполняемые на основе мкэ:

• Статический расчет – определение напряженно-деформированного состояния (перемещений, усилий, напряжений, опорных реакций и других параметров) конструкций при действии статических нагрузок и воздействий (силовых, кинематических, температурных). Задача сводится к решению системы линейных алгебраических уравнений вида⁴:

, (1)

где – матрица жесткости системы,

– вектор неизвестных узловых перемещений,

– вектор узловых нагрузок, соответствующий случаям нагружений или комбинаций нагружений.

По результатам статического расчета выполняют проектирование (подбор сечений, определение армирования и т.п.) конструкций, а также оценивают возможность наступления одного из предельных состояний конструкции.

• Расчет на устойчивость – определение n первых (низших) форм потери устойчивости системы в целом либо ее отдельных частей (элементов), а также минимальных величин нагрузок (или «коэффициентов запаса устойчивости»), при которых происходит потеря устойчивости по этим формам. При этом решается следующая обобщенная задача:

, (2)

где – матрица жесткости системы,

– матрица геометрической жесткости системы, (см. пособие по SCAD)

– вектор i-й формы статической неустойчивости,

– i-е значение критического параметра нагрузки.

Суммарная критическая нагрузка на систему определяется по формуле , где – суммарная нагрузка на систему в рассматриваемой комбинации нагружений⁵.

• Расчет режима свободных колебаний – определение n первых (низших) форм собственных колебаний системы и соответствующих им частот (периодов) колебаний:

, (3)

где – матрица жесткости системы,

– матрица масс системы,

– вектор i-й формы собственных колебаний,

– квадрат i-й собственной круговой частоты системы.

Результат расчета на собственные колебания дает оценку общей жесткости системы, показывает, насколько рационально распределены жесткости по объему сооружения (например, при неудачном расположении диафрагм жесткости возникает закручивание здания в плане – «крутильные» формы колебаний), а также используется для определения реакции сооружения на действие динамических нагрузок в рамках метода разложения по собственным формам.

• Спектральный анализ матрицы жесткости системы – определение собственных значений и векторов матрицы жесткости:

, (4)

где K – матрица жесткости системы,

E – единичная матрица,

– i-й собственный вектор,

– i-е собственное число.

Спектральный анализ используется для установления распределения жесткостей в расчетной модели (иногда при этом обнаруживаются ошибки конструирования или моделирования), определения кинематически подвижных ее частей, а также для оценки вычислительной погрешности решения разрешающей системы уравнений МКЭ.

• Решение динамических задач:

Определение напряженно-деформированного состояния конструкции при действии динамических нагрузок (гармонических, импульсных, ветровых, сейсмических и др.).

, (6)

где – матрица масс,

– матрица демпфирования,

– матрица жесткости,

– вектор неизвестных узловых перемещений, зависящих от времени t,

– вектор узловых нагрузок, зависящих от времени t.