1.2.2 Разрешающая система уравнений.

1. Уравнения равновесия:

2. Уравнения неразрывности деформаций:

3. Закон Гука

После подстановки:

К^-1 – обратная матрица для матрицы жесткости.

Поскольку вычисление обратной матрицы – трудоемкая процедура, то вектор Z получают непосредственным решением системы уравнений.

Проверка:

4. При расчете на внеузловую нагрузку, к расчетным усилиям добавляются усилия от внеузловой нагрузки:

Матричное уравнение - эквивалентно канонической системе уравнений метода перемещений. Каждый элемент матрицы жесткости k_i,j равен коэффициенту r_i,j (т.е. реакции в связи по направлению перемещения Z_i от перемещения Z_j = 1).

1.2.3 Порядок расчета ммп:

1. Выбираем основную систему метода перемещений и строим расчетную схему, определяя направления неизвестных перемещений Z и искомых усилий S.

2. В случае внеузловой нагрузки строим эпюру M_p и приводим нагрузки к узловой. Строим векторы P, S₀.

3. Строим статическую матрицу А и матрицу жесткости К всех элементов.

4. Выполняем операции: и .

5. Решаем систему уравнений равновесия и находим вектор Z.

6. Определяем внутренние усилия .

7. Выполняем проверку .

8. Определяем окончательное значение усилий

9. По найденным усилиям строим окончательные эпюры.

Пример. Проведем данный алгоритм для нашей фермы.

Решаем систему уравнений :

Определяем внутренние усилия:

Метод ММП является промежуточным звеном между классическим методом перемещений и МКЭ. Отличие МКЭ от ММП в методике получения матрицы жесткости системы.

3. Основные принципы метода конечных элементов (мкэ).

Матрица жесткости в МКЭ получается путем суммирования матриц жесткости отдельных конечных элементов, т.е. . А после определения перемещений Z усилия вычисляются поэлементно.

Такой подход позволяет один раз получить матрицы жесткости типовых (библиотечных) элементов, представить конструкцию как их совокупность и на основе заданного алгоритма автоматически составлять матрицу жесткости для каждого из них по задаваемым пользователем параметрам.

1.3.1 Атрибуты конечного элемента.

1. Собственная размерность. Конечные элементы могут описываться одной, двумя или тремя пространственными координатами в зависимости от размерности задачи, для решения которой они предназначены. Соответствующее число внутренних или локальных координат называется собственной размерностью элемента. В расчетах могут использоваться также специальные элементы с нулевой размерностью, такие как, точечные массы или сосредоточенные упругие элементы (пружины).

2. Узловые точки. Каждый элемент описывается множеством характерных точек, называемых узловыми точками или узлами.

3. Геометрия элемента. Геометрия элемента определяется расположением узловых точек. Большинство элементов, используемых в расчетах, имеют достаточно простую геометрическую форму. Например, в одномерном случае элементы обычно представляют собой прямолинейные отрезки или сегменты кривых линий; в двумерном случае элементы имеют трехстороннюю или четырехстороннюю форму; в трехмерных задачах наиболее распространены такие геометрические фигуры, как тетраэдры, призмы и гексаэдры (Рис. 8).

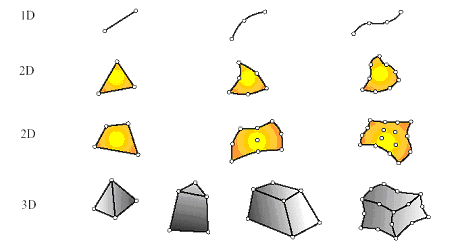
Рис. 8. Основные типы конечных элементов для одно-, дву- и трехмерных задач механики.

4. Степени свободы. Степени свободы определяют физическое состояние элемента. Благодаря общим степеням свободы в соседних элементах осуществляется сборка модели и формирование глобальной системы конечно-элементных уравнений.

5. Узловые силы. Система узловых сил полностью соответствует степеням свободы элемента и выражается с помощью глобального вектора узловых сил.

6. Определяющие соотношения. Для конечных элементов, используемых в механических расчетах, определяющее соотношение задает поведение материала, из которого изготовлена конструкция. Например, в качестве такого соотношения во многих случаях используется обобщенный закон Гука, связывающий тензор деформаций и тензор напряжений в точке. Для линейного упругого стержневого элемента достаточно задать один модуль Юнга Е и один коэффициент температурного расширения.

7. Свойства сечения. К свойствам сечения относятся площади и моменты инерции одномерных и двумерных конечных элементов, таких как балки, стержни, пластины. В эту группу также входит толщина пластин и оболочек. При построении конечного элемента свойства сечений считаются заданными и входят в результирующую матрицу жесткости элемента.

Например, при решении плоских задач стержневые элементы могут быть только трех типов:

• Шарнирно опертый стержневой элемент;

• Балочный элемент, жестко защемленный по обоим концам;

• Комбинированный элемент (шарнир на одном конце и заделка на другом).