Югорский государственный университет

Задачи для самостоятельного решения по физике

для студентов групп 1120б и 1121б ИСУиИТ в первом семестре 2012 года

МЕХАНИКА

Кинематика

1. Кинематические уравнения движения двух материальных точек имеют вид 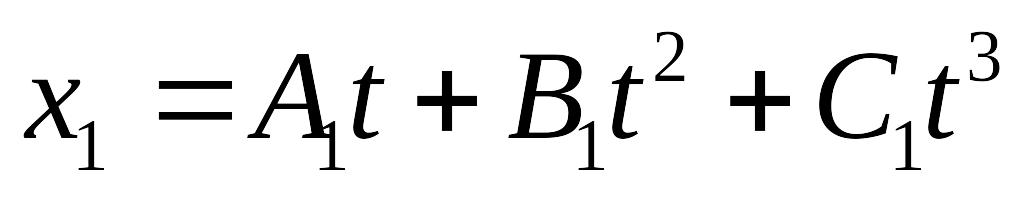и 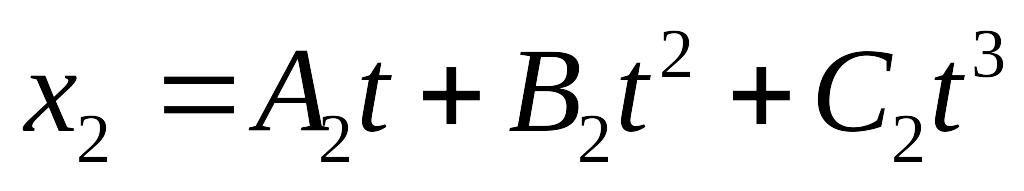, где В₁ = В₂, С₁ = -2 м/с², С₂ = 1 м/с² . Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а1 и а2 для этого момента.

t = 0; 2) а₁ = -4 м/с²; 3) а₂= 2 м/с²)

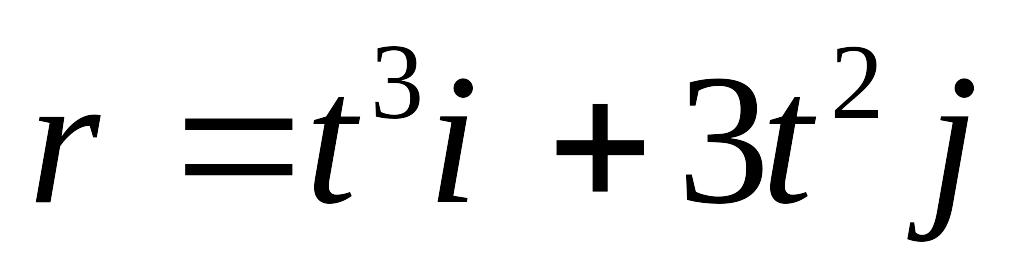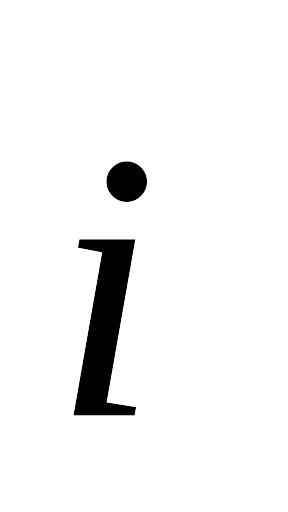2. Радиус-вектор материальной точки изменяется со временем по закону , где и - орты осей x и y. Определите для момента времени t = 1 c: 1) модуль скорости; 2) модуль ускорения.

( 1)  = 6,7 м/с; а = 8,48 м/с²)

3. Зависимость пройденного пути S от времени t дается уравнением S = A – Bt + Ct², где А = 6 м, В = 3 м/с и С = 2 м/с². Найти среднюю скорость и среднее ускорение тела в интервале времени от 1 до 4 с.

( 7м/с, 4 м/с²)

4. Закон движения материальной точки имеет вид x = b₁ + c₁t, y = c₂t + d₂t², z = 0, где b₁ = -9 м; с₁ = 3 м/с; с₂ = 4 м/с; d₂ = -1 м/с². Построить графики зависимости x(t) и y(t) и траекторию точки за первые 5 с движения. Найти векторы скорости, ускорения и угол между ними в момент времени t₁ = 2 c и t₂ = 4 c. На плоскости XOY построить траекторию движения материальной точки и векторы скорости и ускорения для t₁ и t₂ .

5. Закон движения материальной точки имеет вид x = b₁t +d₁t³, y = b₂t + c₂t², z = 0, где b₁ = 27 м/с; d₁ = -1 м/с³; b₂ = 32 м/с; с₂ = -8 м/с². На плоскости XOY построить траекторию движения точки в первые 6 с. Определить касательное и нормальное ускорения и радиус кривизны траектории в момент времени t₁=2c.

6. Материальная точка движется прямолинейно. Модуль её скорости изменяется со временем по закону v = l,0t², где v - скорость, м/с; t - -время, с. Вычислить путь, пройденный точкой за первые 10 с движения и среднее значение скорости в интервале от 5 до 10 с.

( 0,33 км; 58 м/с)

7. Два автомобиля, выехали одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного пути задается уравнениями s₁ = At + Bt² и s₂ = Ct + Dt² + Ft³ . Определите относительную скорость автомобилей.

8. Велосипедист проехал первую половину времени своего движения со скоростью v₁ = 16 км/ч, вторую половину времени – со скоростью v₂ = 12 км/ч. Определите среднюю скорость движения велосипедиста.

9. В течение времени τ скорость тела задается уравнением вида v = A+Bt+Ct² (0≤ t ≤ τ). Определите среднюю скорость за промежуток времени τ.

10. Трамвай движется на прямолинейном участке между остановками с ускорением, изменяющимся по закону а = a₀ - bs, где a₀ и b - положительные постоянные; s - пройденный путь. Найти расстояние между этими остановками.

( 2 a₀/b.)

11. Частица движется в плоскости хОу из точки с координатами х = у = 0 со скоростью v = ai + bxj, где а и b - некоторые постоянные; i и j - орты осей х и у. Найти уравнение её траектории.

( у = (b/2а)х²)

12. Скорость автомобиля при экстренном торможении изменялась по закону v = 49 – 1,0t² , где v - скорость, м/с; t - время, с. Определить время торможения и тормозной путь.

( 7,0 с и 0,23 км.)

13. С башни брошено тело в горизонтальном направлении со скоростью 15 м/с. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через 2 с после начала движения.

( 0,1 км. )

14. Материальная точка движется по закону r = 4t²i +3tj + 2k , где i, j, k -орты осей x, y_t z; r- радиус-вектор, м; t - время, с, Определить: 1)скорость как функцию времени; 2) модуль скорости в момент времени t = 2,0 с; 3) ускорение точки.

( 16 м/с; в м/с²)

15. Частица движется в плоскости хОу из точки с координатами х = у = 0 со скоростью v = ai + bxj, где а и b - некоторые постоянные; i и j - орты осей х и у. Найти уравнение её траектории.

( у = b/2а)х²)

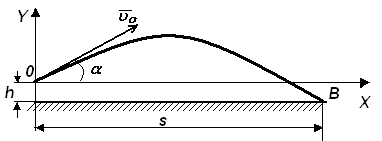
16. Камень, брошенный с высоты h = 2,1 м под углом  = 45^о к горизонту. Падает на землю на расстоянии s = 42 м (по горизонтали) от места бросания (см. рис. 1). Найти начальную скорость камня, время полета и максимальную высоту подъема над уровнем земли. Определить также радиусы кривизны траектории в верхней точке и в точке падения камня на землю.

17. При падении камня в колодец его удар о поверхность воды доносится через t = 5 с. Принимая скорость звука  = 330 м/с, определите глубину колодца

18. Колесо вращается с постоянным угловым ускорением  = 3 рад/с². Определите радиус колеса, если через t = 1 c после начала движения полное ускорение колеса а = 7,5 м/с².

( R = 79 м)

19. Колесо автомашины вращается равнозамедленно. За время t = 2 мин оно изменило частоту вращения от 240 до 60 мин -1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.

( 1)  = 0,157 рад/с2; 2) N = 300)

20. Скорость тела изменяется по закону 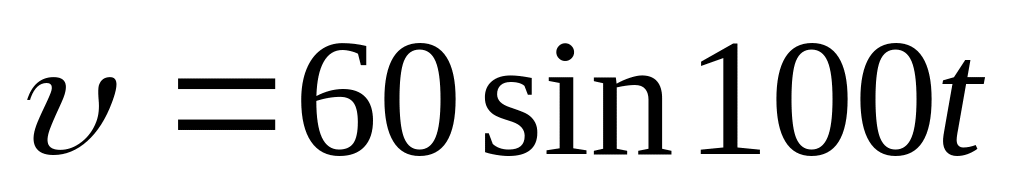, где v - скорость, мм/с; t ~ время, с. Определить зависимость смещения от времени, а также максимальные значения скорости и ускорения тела.

(6,0 см/с; 6,0 м/с²)

21. Движение тела задано уравнениям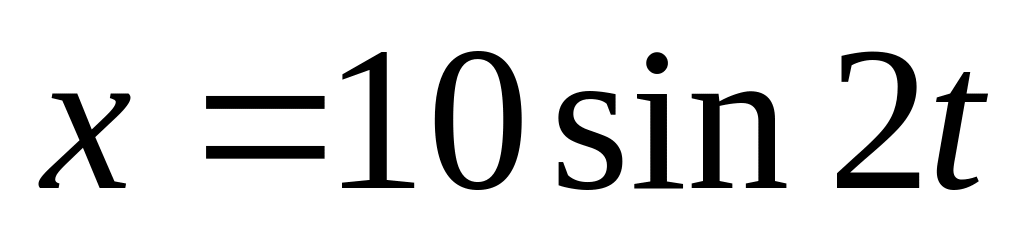и: и 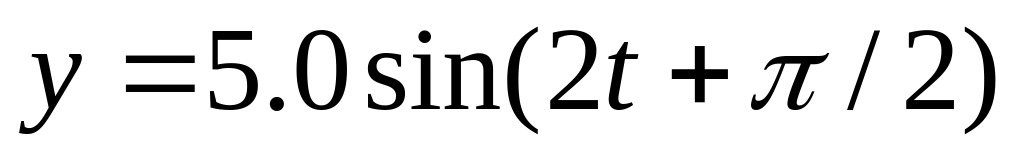, где x и у - смещения, см; t - время, с. Найти уравнение траектории и скорость тела в момент времени 0,50 с.

( ; 1,4 см/с)

22. Точка двигалась в течение времени t₁ = 15 с со скоростью ₁ = 5 м/с, в течение t₂ — 10 с со скоростью ₂ = 8 м/с и в течение t₃ = 6 с со скоростью ₃ = 20 м/с. Какова средняя путевая скорость  точки?

(_ср = 8,9м/с)

23. Движение точки по прямой задано уравнением х = 2t — 0,5t². Определить среднюю путевую скорость _ср точки в интервале времени от t_l = 1 с до t₂ ⁼ 3 с.

( = 0,5 м/с)

24. Точка движется по прямой согласно уравнению х = 6t — 0.125t³. Определить среднюю путевую скорость _cp точки в интервале времени от t_l = 2 с до t₂ = 6 с.

(_cp = 3 м/с)

25. Самолет пролетает расстояние s₁ = 500 км на восток от города А в город В за t₁ = 45 мин, затем поворачивает на юг и преодолевает расстояние s₂ = 1000 км от города В до города С за 1,5 ч,

Определить: 1) величину и направление вектора перемещения самолета из А в С; 2) величину и направление вектора средней скорости; 3) среднюю путевую скорость. Направление задается азимутом а, т. е. углом между направлением на север и данным вектором, отсчитывается по часовой стрелке, т, е. от севера к востоку

(1) = 1118,0 км;  = 153,4°; 2) = 496,9 км;  = 153,4°; 3) _cp – 666_.7 км/ч)

26. За 3,5 ч воздушный шар снесло на s₁ = 21,5 км к северу, затем на s₂ = 9_.,7 км к востоку, причем высота его подъема увеличилась на h = 2_,88 км. Найти: 1) величину вектора его средней скорости; 2) угол  вектора средней скорости с горизонтальной плоскостью.

(1) = 6,79 км/ч; 2)  = 6,96°)

27. Предполагается, что самолет, имеющий скорость  = 550 км/ч, должен лететь по прямой под углом  = 33,0° к северу от направления на восток. Однако с севера дует постоянный ветер со скоростью _l = 120 км/ч. В каком направлении должен лететь самолет?

(Под углом  = 43,5° к северу от направления на восток)

28. Определить время полета самолета между двумя пунктами, находящимися на расстоянии s = 500 км, если скорость самолета относительно воздуха ₀ = 100 м/с, а скорость встречного ветра, направленного под углом  = 30° к прямой, соединяющей эти пункты, равна ₁ = 30 м/с. Во сколько раз уменьшится время полета, если ветер будет попутным, а его скорость направлена под углом  = 30° к направлению движения? Под каким углом к направлению движения должна быть направлена скорость самолета в обоих случаях?

(1,9 ч; 1,7 раз; 9°; 9°)

29. Велосипедист начал движение и в течение времени t₁ = 5 с ехал с ускорением а = 1 м/с², затем в течение следующих t₂ = 6 с двигался равномерно и последние 25 м - равнозамедленно до остановки. Найти среднюю скорость на всем пути.

( = 3,2 м/с)

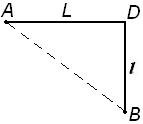
30. По прямолинейному шоссе ACD едет машина, которой необходимо за кратчайшее время добраться из пункта А в пункт В, расположенный в поле на расстоянии l = 500 м от дороги (смотри первый рисунок). Известно, что скорость машины по полю в n = 2 раза меньше скорости машины по шоссе. На каком расстоянии s от точки D следует свернуть с шоссе? Проанализировать роль расстояния l между пунктами А и D, лежащими на шоссе.

(s = 288,7 м; при L < s машина из А сразу должна съехать с шоссе и зять курс на пункт В)

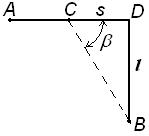
31. Из пункта A, находящегося на шоссе, необходимо попасть за кратчайшее время в пункт B, находящееся в поле на расстоянии D от шоссе. Известно, что скорость машины по полю в n раз меньше скорости по шоссе. На каком расстоянии от точки В следует свернуть с шоссе.

32. Скорость света в вакууме равна c, а в среде v = c/n₁ , где n₁ – абсолютный показатель преломления света. Обосновать закон преломления света.

33. Зависимость пройденного точкой пути от времени задана уравнением s = 0,14t² + 0,01t³ (здесь и далее в подобных задачах время измеряется в секундах, расстояние — в метрах). Определить: 1) через какое время t₁ ускорение точки будет равно а = 1 м/с²; 2) мгновенную скорость _l в этот момент времени; 3) среднюю путевую скорость _cp за промежуток времени от t = 0 до t₁.

(t_l = 12 с; 2) ₁, = 7,68 м/с; 3) _ср = 3,12 м/с)

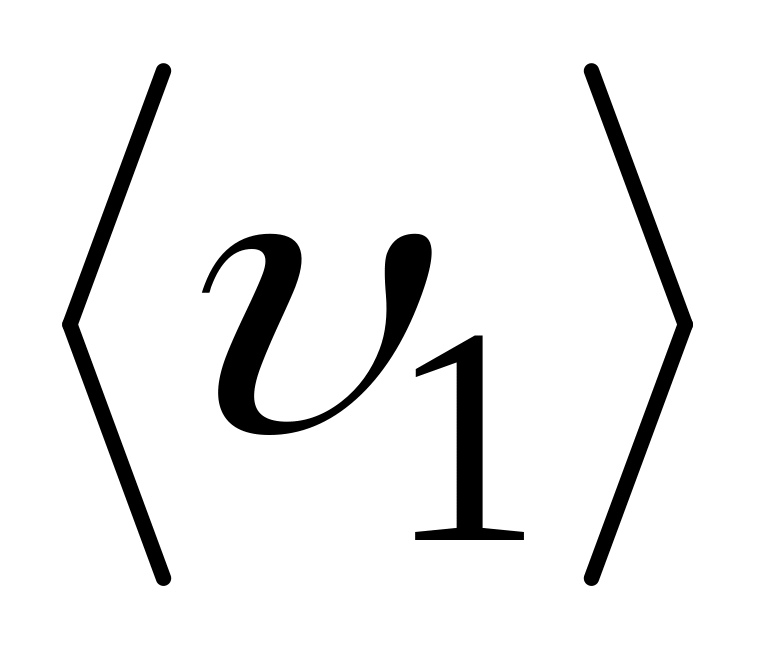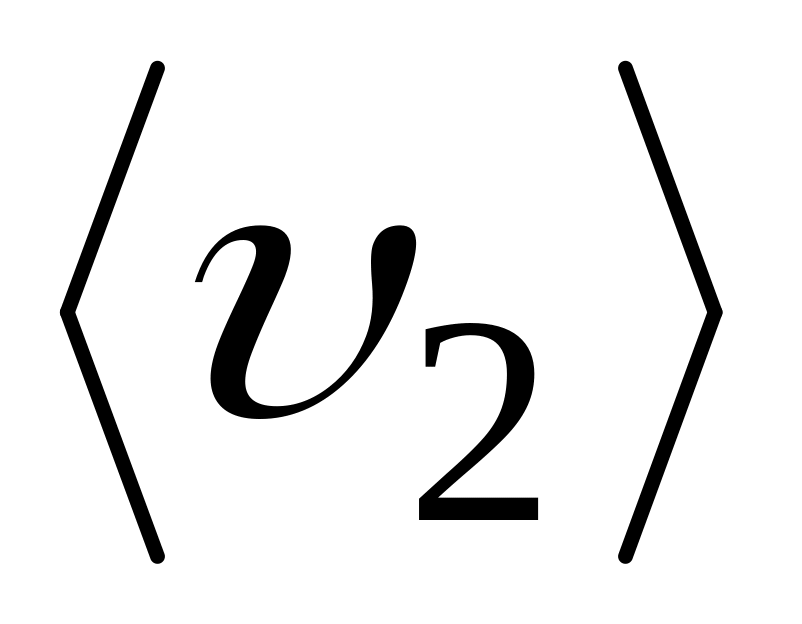34. Положение объекта на прямой линии в зависимости от времени дается уравнением х = at + bt² + ct³, где а = -8 м/с; b = 6 м/с², с = - 1 м/с³. Найти среднюю скорость объекта на временном интервале от t₀ = 0 с до t₂ = 2 с. Сравнить ее со средними скоростями на интервале от t₀ = 0 с до t₁ = 1 с и на интервале от t₁ = 1 с до t₂ = 2 с.

( = 0 м/с; = -3 м/с; = 3 м/с)

35. Две материальные точки движутся согласно уравнениям x₁ = 4t + 8t² -16t³; х₂ = 2t – 4t² + t³. В какой момент времени t₁ ускорения этих точек будут одинаковы? Найти скорости ₁, и ₂ точек в этот момент.

(t₁ = 0,235 с; ₂ = 5,11 м/с; ₂ = 0,284 м/с)

36. Движение двух материальных точек выражается уравнениями х, = 20 + 4t - 4t²; x₂ = 2 + t•

37. + 0,5t². В какой момент времени t₁ скорости этих точек будут одинаковыми? Определить скорости ₁ и ₂ и ускорения а₁, и а₂ точек в этот момент.

(t₁ = 0,333 с; ₁ = ₂ = 1,33 м/с; а₁= -8 м/с², а₂ = 1 м/с²)

38. Зависимость пройденного телом пути s от времени t дается уравнением s = 1t - 3t² + 4t³. Найти расстояние, пройденное телом, скорость и ускорение тела через 2 с после начала движения.

(s = 24 м;  = 38 м/с; а = 42 м/с²)

39. Замаскированный полицейский автомобиль, движущийся с постоянной скоростью ₁ = 80 км/ч, обогнал лихач. Если полицейский автомобиль, ускоряясь равномерно с ускорением а = 3 м/с², догнал его через время t = 6 с, то какой была скорость лихача?

( = 108 км/ч)

40. Замаскированный полицейский автомобиль, движущийся с постоянной скоростью ₁ = 80 км/ч, обогнал лихач, несущийся со скоростью 100 км/ч. Ровно через t = 1 с после обгона полисмен нажал на акселератор. Если ускорение полицейского автомобиля а = 3 м/с², то сколько времени понадобится полицейским, чтобы догнать лихача (будем полагать, что он движется с постоянной скоростью)?

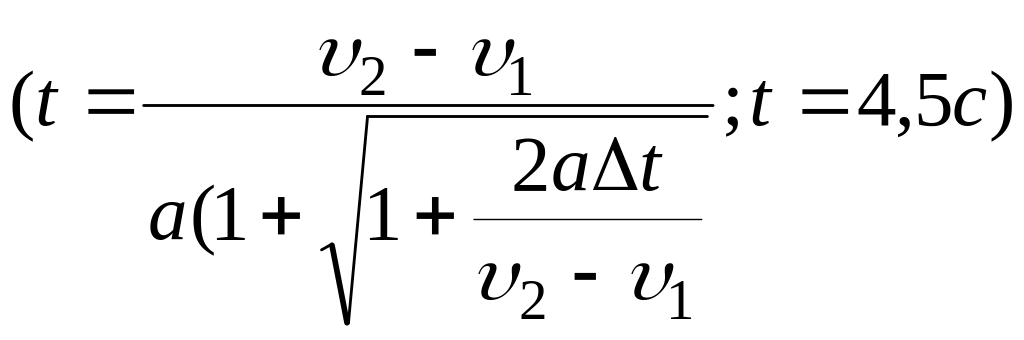
41. Автомобиль, движущийся со скоростью ₀ = 50 км/ч, врезается в дерево; передняя часть автомобиля деформируется, а тело водителя перемещается на l = 0,7 м и останавливается. Определить среднее ускорение водителя во время этого столкновения. Выразить ответ в единицах, кратных ускорению свободного падения. g = 9.8 м/с².

(a = ²₀ /(2l); a = 14g)

42. Поезд длины l = 350 м начинает двигаться по прямому пути с постоянным ускорением а = 3,010^-2 м/с². Через t = 30 с после начала движения был включен прожектор локомотива (событие 1), а через τ = 60 с после этого — сигнальная лампа в хвосте поезда (событие 2). Найти расстояние между этими событиями в системах отсчета, связанных с поездом и Землей. Как и с какой постоянной скоростью  относительно Земли должна перемещаться некоторая K-система отсчета, чтобы оба события произошли в ней в одной точке?

( = (l/) – a(/2 + t) )

43. Машина едет по шоссе за грузовиком с той же скоростью. Между двойными шинами заднего колеса грузовика застрял камень. На каком расстоянии от грузовика должен ехать легковой автомобиль, чтобы камень, вырвавшийся из-под колеса грузовика, не попал в нее?

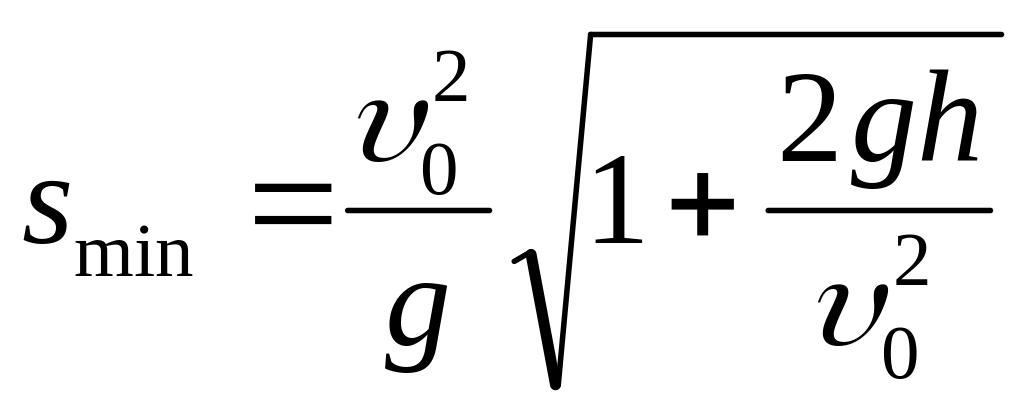( , где ₀ – скорость автомобилей, h  1 м – высота камня в момент отрыва: s  11 м (₀ = 36 км/ч); s  40 м (₀ = 72 км/ч); s  90 м (₀ = 108 км/ч)

44. Точка движется по кривой с постоянным тангенциальным ускорением a_ = 0,5 м/с². Определить полное ускорение а точки на участке кривой с радиусом кривизны R = 3 м_; если точка движется на этом участке со скоростью  = 2 м/с.

(а = 1,42м/с²)

45. Уравнение вращения колеса радиусом R = 0,5 м имеет вид  = At + Bt⁵, где А = 2 рад/с; В = 0,5 рад/с⁵. Определить полное ускорение в момент t = 1 с точки, находящейся на ободе колеса.

(a =11,3 м/с²)

46. Точка начинает движение по окружности радиусом R = 10 м. Пройденный ею путь зависит от времени по закону s = At + Bt³, где А = 8 м/с, В=1 м/с³. Определить скорость и полное ускорение точки b момент t = 2 с,

( = 20 м/с; а = 41 ,8 рад/с²)

47. По истечении времени t = 2 с после начала равноускоренного вращения вектор ускорения точки, лежащей на ободе, составляет угол  = 60° с направлением линейной скорости этой точки. Найти угловое ускорение колеса.

(s = 0,43 рад/с²)

48. Материальная точка начинает двигаться по окружности радиуса r = 0,1 м с постоянным касательным ускорением a_ = 0,004 м/с² . Через какой промежуток времени вектор ускорения образует с вектором скорости 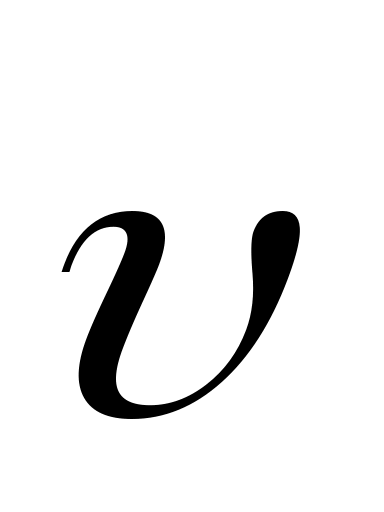угол , равный: а) 60; б) 80^о (см. рис. 2)? Какой путь пройдет за это время движущаяся точка? На какой угол повернется радиус-вектор, проведенный из центра окружности к движущейся точке, если в начальный момент времени он направлен вертикально вверх? Движение происходит по часовой стрелке.

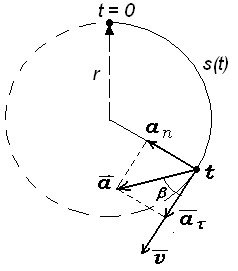
49. Материальная точка начинает двигаться по окружности радиусом r =12,5 см с постоянным тангенциальным ускорением a_τ = 0,5 см/с². Определите: 1)момент времени, при котором вектор ускорения a образует с вектором скорости v угол α = 45 ⁰ ; 2) путь, пройденный за это время движущейся точкой.

50. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = At² (A=0,1рад/с²). Определите полное ускорение a точки на ободе диска к концу второй секунды после начала движения, если линейная скорость этой точки в этот момент равна 0,4 м/с.

51. За время t колесо поворачивается на угол , зависящий от времени по закону  = 5,0t + 3,0t² - 4,5t⁴, причем  измеряется в радианах, a t - в секундах. Определить: 1) среднюю скорость колеса; 2) среднее угловое ускорение за промежутки времени от t = 2,0 с до t = 3,0 с; 3) выражение для мгновенной угловой скорости ; 4) выражение для мгновенного углового ускорения ; 5) вычислить значения мгновенной угловой скорости и мгновенного углового ускорения в момент времени t - 3,0 с.

    1. -280 рад/с; 2) -340 рад/с²; 3) 5,0 + 6,0t- 18t³; 4) 6 – 54t²; 5) -463 рад/с, -480 рад/с²)

52. Колесо диаметром 40см вращается с постоянным ускорением так, что за 3,6 с частота вращения возрастает от 80 до 300 об/мин. Вычислить: 1) угловое ускорение колеса; 2) радиальную и тангенциальную составляющие вектора линейного ускорения точки на ободе колеса через 2,0 с после начала ускоренного движения колеса.

(1) 6,4 рад/с²; 2) 66 м/с²; 2,6 м/с²)

53. Два резиновых диска расположены рядом друг с другом так, что их края соприкасаются. Первый диск радиусом R₁ = 3,0 см начинает вращаться с угловым ускорением  = 0,88 рад/с² и заставляет вращаться второй диск радиусом R₂ = 5,0 см, причем второй диск вращается относительно первого диска без проскальзывания. Определить: 1) за какой промежуток времени второй диск достигает угловой скорости 33 об/мин, если в начальный момент он находился в покое; 2) угловое ускорение второго диска.

(1)6,5 с; 2) 0,53 рад/с²)

54. Колеса автомобиля совершают 55 оборотов за промежуток времени, в течение которого скорость равномерно уменьшилась от 80 км/ч до 55 км/ч. Диаметр колеса равен 1,0 м. Определить: 1) чему было равно угловое ускорение колеса; 2) если автомобиль продолжает замедляться с тем же ускорением, то сколько времени ему понадобится до полной остановки.

(1)-1,5 рад/с²; 2) 20 с)

55. Тело брошено со скоростью ₀ = 10 м/с под углом  = 30° к горизонту. Найти радиус кривизны через t = 1 с.

(R = 6,3м)

56. На большой горизонтальной поверхности закреплена маленькая пушка, которая выбрасывает снаряд со скоростью ₀ = 50 м/с. На расстоянии l = 50 м от пушки находится вертикальная стена высотой h = 25 м. Поставлена задача — забросить снаряд как можно дальше за стену. Под каким углом а к горизонту следует стрелять и как далеко улетит снаряд за стену? (g = 10 м/с², сопротивление воздуха не учитывать.)

( = 33°; s = 227 м)

Динамика

57. Тело массой m движется в плоскости xy по закону x = A cos t, y = B sin t, где A, B, и – некоторые постоянные. Определите модуль силы, действующей на это тело.

58. Тело массой m = 2 кг движется прямолинейно по закону 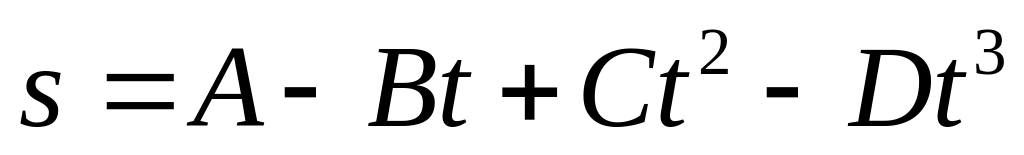(С = 2 м/с², D = 0,4 м/с²). Определите силу, действующую на тело в конце первой секунды движения.

( F = 3,2 H.)

59. Тело массой m = 2 кг падает вертикально с ускорением a = 5 м/с². Определите силу сопротивления при движении этого тела.

( F_сопр = 9,62 Н.)

60. Снаряд массой m = 5 кг, вылетевший из орудия, в верхней точке траектории имеет скорость  = 300 м/с² . В этой точке он разорвался на два осколка, причем больший осколок массой m₁ = 3 кг полетел в обратном направлении со скоростью ₁ =100 м/с. Определите скорость ₂ второго, меньшего, осколка.

( ₂ = 900 м/с)

61. Под действием какой силы при прямолинейном движении тела изменение его координаты со временем происходит по закону 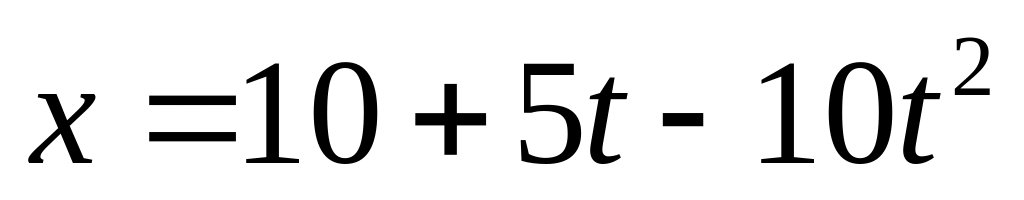? Масса тела 2 кг.

62. Тело массой m = 70 кг движется под действием постоянной силы F = 63 Н. Определите, на каком пути s скорость этого тела возрастает в n = 3 раза по сравнению с моментом времени, когда скорость тела была равна ₀ = 1,5 м/с.

( s = 10 м)

63. Два тела m₁= 0,1 кг и m₂ = 0,5 кг связаны нерастяжимой нитью длиной l, перекинутой через блок радиуса R = 0,1 м. Определить координаты x₁ и x₂ этих тел через 5 секунд после начала движения, если x₀ = 3,314 м (см. рис.)? Ускорение свободного падения g = 10 м/с².

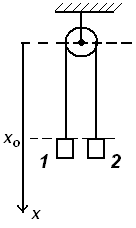
64. Простейшая машина Атвуда, применяемая для изучения законов равноускоренного движения, представляет собой два груза с не равными массами m₁ и m₂ (например m₁ > m₂), которые подвешены на легкой нити, перекинутой через неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, определите: 1) ускорение грузов; 2) силу натяжения нити T; 3) силу, F действующую на ось блока

65. Пуля массой m = 15 г, летящая с горизонтальной скоростью  = 0,5 км/с, попадает в баллистический маятник М = 6 кг и застревает в нем. Определите высоту h, на которую поднимется маятник, откачнувшись после удара.

( h = 7.9 см)

66. На спокойной воде пруда перпендикулярно берегу и носом к нему стоит лодка массой М и длиной L. На корме стоит человек массой m. На какое расстояние s удалится лодка от берега, если человек перейдет с кормы на нос лодки? Силами трения и сопротивления пренебречь.

67. Частица массой 10 г совершает гармонические колебания с периодом 2,0 с. Полная энергия колеблющейся частицы 0,10 мДж. Определить амплитуду колебаний и наибольшее значение возвращающей силы.

(45 мм; 4,4 мН)

68. Определить угловую частоту колебаний груза массой 0,80 кг, закрепленного на двух пружинах между горизонтальными опорами. С одной стороны груза жёсткость пружины равна 1500 Н/м, с другой - 500 Н/м.

(50 с-¹)

69. Вычислить ускорение падающего груза а = 2h/t², где h - высота, с которой падает тело, измерена линейкой (1 мм/дел.); t - время падения, измерено секундомером (0,2 с/дел.): h, см 87,4 87,5 87,3; t, с 7,8 8,0 7,8 7,6 7,8.

70. Определить максимальную кинетическую энергию материальной точки массой 2,0 г, совершающую гармонические колебания с амплитудой 4,0 см и частотой 5,0 Гц.

(1,6 мДж)

71. Груз массой т подвешен на двух параллельных пружинах, жёсткости которых k1 и k2. Определить период колебаний груза. Массами пружин пренебречь.

72. Точка движется замедленно по окружности радиусом R так, что её тангенциальное и нормальное ускорения равны по модулю в каждый момент времени. В начальный момент скорость точки равна yo. Определить зависимость скорости точки и модуля полного ускорения от пройденного пути.

( = ₀ exp(-s /К); а = (₀² /R)exp(-2s/R) )

73. Тело массой 100 г совершает гармонические колебания с амплитудой 50,0 мм, периодом 10,0 мс и Нулевой начальной фазой. Определить частоту колебаний, угловую частоту, максимальные значения скорости и ускорения, энергию колебательной системы.

(100 Гц; 628 с^-1; 31,4 м/с;19,7 км/с²; 49,3 Дж)

74. Диск радиусом 24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно к плоскости диска. Определить период колебаний.

(1,2 с)

75. Материальная точка совершает колебания согласно уравнению х = 5 sin 2t, где х - смещение, см; t - время, с. Найти момент времени (ближайший к началу отсчета), в который потенциальная энергия точки равна 0,1 мДж, а возвращающая сила равна 5 мН. Определить фазу колебаний в этот момент времени.

(0,5 с; 0,9 рад)

76. Колебательная система успевает совершить 100 колебаний за 100 с. За это же время амплитуда уменьшается в 2,72 раза. Найти коэффициент затухания колебаний и логарифмический декремент затухания.

(0,0100 с^-1; 0,0100)

77. Скорость автомобиля при экстренном торможении изменялась по закону  = 49 – 1,0t² , где - скорость, м/с; t - время, с. Определить время торможения и тормозной путь.

(7,0 с и 0,23 км)

78. Точка участвует одновременно в двух колебаниях с одинаковым периодом и одинаковыми начальными фазами. Амплитуды колебаний равны 3 и 4 см. Найти амплитуду результирующего колебания, если 1) колебания совершаются в одном направлении; 2) колебания взаимно перпендикулярны.

(7 см; 5 см)

79. Математический маятник длиной 50 см совершает свободные колебания в среде с коэффициентом затухания 0,90 с^-1. Определить время, за которое амплитуда колебаний уменьшится в пять раз.

(1,8 с)

80. Частица движется с постоянной по модулю скоростью v по параболической траектории у = k x², где k – положительная постоянная. Определить ускорение частицы в точке х = 0,

(а = 2kv²)

81. Брусок массой т находится на доске массой М, которая лежит на гладкой горизонтальной плоскости. Коэффициент трения между бруском и доской равен k. К доске приложили горизонтальную силу F, зависящую от времени по закону F = At, где А - постоянная. Найти момент времени t₀, когда начнется движение бруска относительно доски.

82. Небольшое тело соскальзывает с вершины гладкой сферы радиусом R. Найти скорость тела в момент отрыва от поверхности сферы, если его начальная скорость пренебрежимо мала.

83. Водитель начинает тормозить на расстоянии 10 м от препятствия. Сила трения в тормозных колодках колес равна 17 кН. Какой может быть скорость машины массой 1500 кг, чтобы она остановилась перед препятствием? Потери энергии на трение колес о дорогу не учитывать.

( < 54 км/ч)

84. На краю неподвижной скамьи Жуковского диаметром 0,8 м и массой 6,0 кг стоит человек массой 60 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает летящий на него мяч массой 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии 0,4 м от оси скамьи. Скорость мяча 5 м/с.

(0,1 рад/с)

85. По рельсам фуникулера, проложенным с уклоном  к горизонту, опускается вагон массой т. Скорость вагона на всём пути равна v, время торможения перед остановкой - . Найти натяжение каната при торможении. Коэффициент трения между вагоном и рельсами равен k,

86. Автомобиль начинает движение с постоянным тангенциальным ускорением а_ по горизонтальной дороге, описывая окружность радиусом R. Коэффициент трения между колесами машины и дорогой равен k. Какой путь s пройдет автомобиль без скольжения, если начальная скорость его была равна нулю?

87. Горизонтальная платформа массой 100 кг вращается вокруг вертикальной оси, проходящей через её центр, совершая 10 об/мин. Человек массой 60 кг стоит на краю платформы. С какой частотой начнет вращаться платформа, если человек перейдет от края: платформы к центру? Считать платформу однородным диском.

(0,37 об/с)