
1.14.2. Взаимосвязь прямой и двойственной задач и обоснование правил алгоритма двойственного симплекс-метода
Цель приводимого здесь материала – обосновать правила алгоритма двойственного симплекс-метода, суть которого заключается в следующем:
- предлагается решать исходную задачу по правилам применения алгоритма симплекс-метода к двойственной задаче, т.е. предлагается работать со структурами данных исходной задачи, а в качестве правил работы с ними использовать правила симплекс-метода, применяемого к решению двойственной ЗЛП.
Основная цель данного раздела – сформулировать положения, позволяющие обосновать работу нового алгоритма решения ЗЛП - алгоритма двойственного симплекс-метода.
Приводимые ниже положения, определяющие взаимосвязь прямой и двойственной задач могут быть сформулированы как ряд теорем с соответствующими доказательствами. Ставя перед собой задачу рассмотрения прикладных вопросов, сформулируем эти положения в виде перечня свойств прямой и двойственной задач.
Между решениями прямой и двойственной ЗЛП существует следующая взаимосвязь:
а)
если
![]() и
и
![]() ,
то
,
то
![]() ; (1.99)
; (1.99)
б) если в одной из задач существует оптимальное решение, то соответствующее оптимальное решение существует и в другой задаче, причем
![]() , (1.100)
, (1.100)
в) между следующими исходами решения прямой и двойственной задачи существует взаимно однозначное соответствие:
{![]() «
(
«
(![]() )},
{(
)},
{(![]() )
«
)
«
![]() };
};
г)
псевдоплан является допустимым решением
исходной задачи только в том случае,
если соответствующий сопряженный базис
является оптимальным базисом прямой
задачи (![]() ).
).
Другими словами, для всех сопряженных базисов, кроме одного, соответствующее базисное решение исходной задачи (псевдоплан) является недопустимым. Этим и определяется использование указанного термина.
Можно показать, что найденное оптимальное решение одной из задач однозначно определяет оптимальное решение другой.
Если некоторая компонента псевдоплана
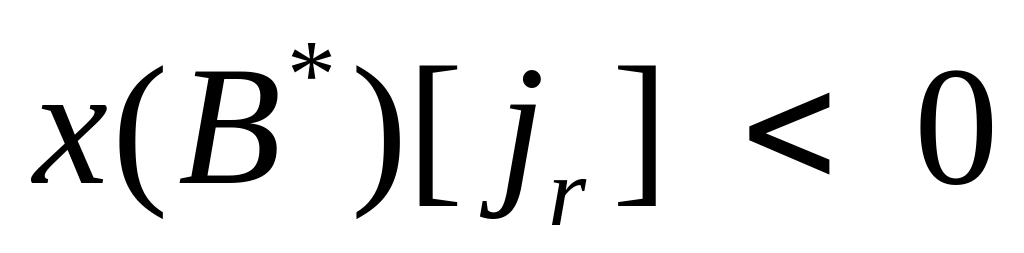 ,
то вывод ее из базисного множества
,
то вывод ее из базисного множества
 соответствует перемещению в пространстве
двойственных переменных при котором
целевая функция двойственной задачи
уменьшается.
соответствует перемещению в пространстве
двойственных переменных при котором
целевая функция двойственной задачи
уменьшается.
Максимальный шаг
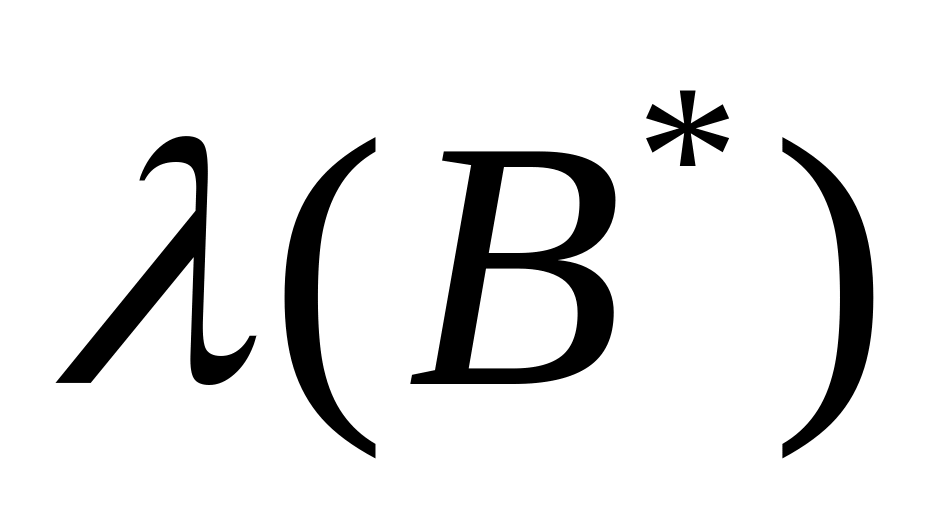 ,
который можно сделать из
,
который можно сделать из
 в выбранном в соответствии с п.2
направлением без выхода из
в выбранном в соответствии с п.2
направлением без выхода из
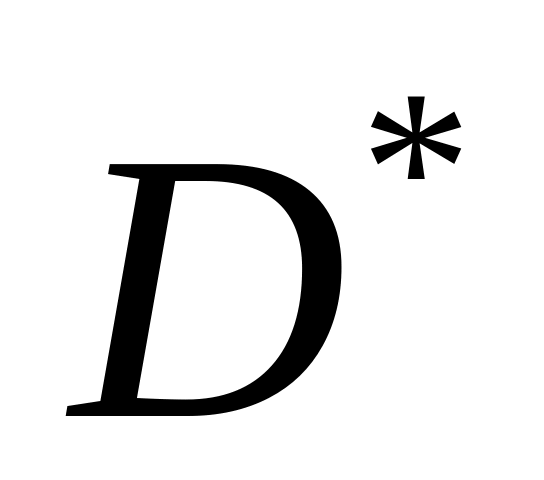 определяется следующим соотношением,
формируемым на основе матрицы
определяется следующим соотношением,
формируемым на основе матрицы
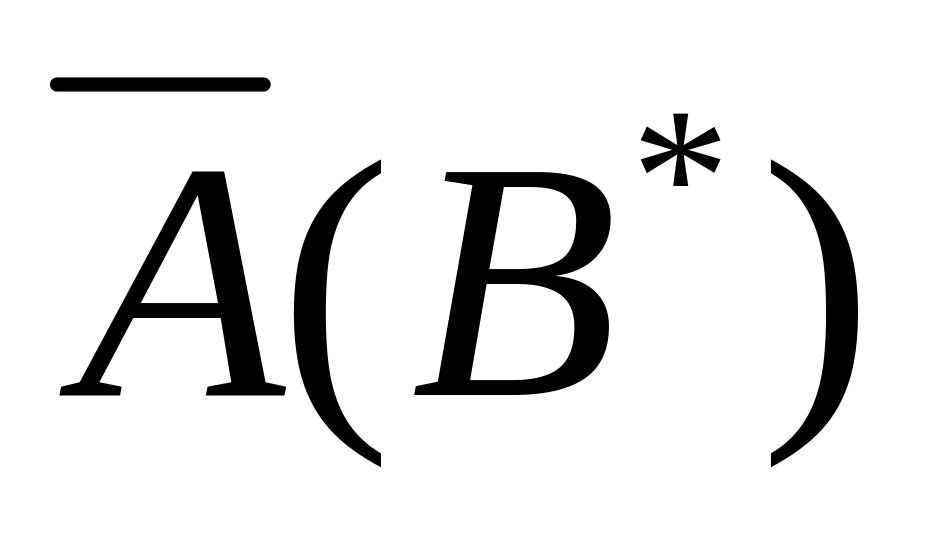 прямой задачи:
прямой задачи:
![]() (1.105)
(1.105)
где
![]() . (1.106)
. (1.106)
При этом осуществляется переход к новому сопряженному базису
![]() . (1.107)
. (1.107)
Если
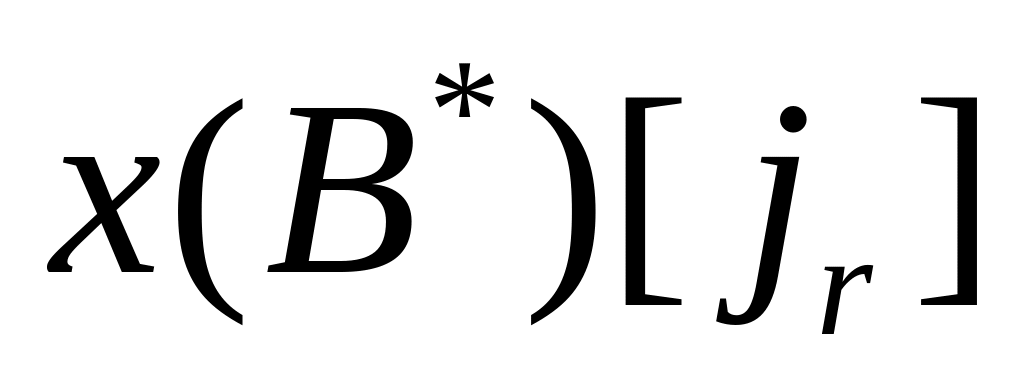 <0
и
<0
и
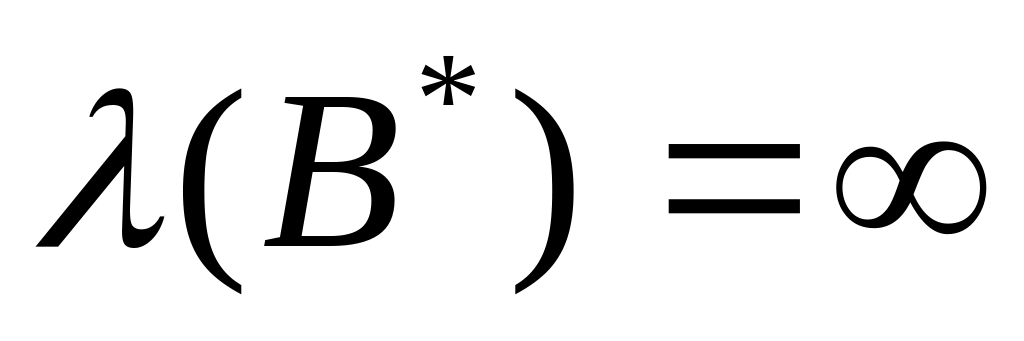 (последнее выполняется при
(последнее выполняется при
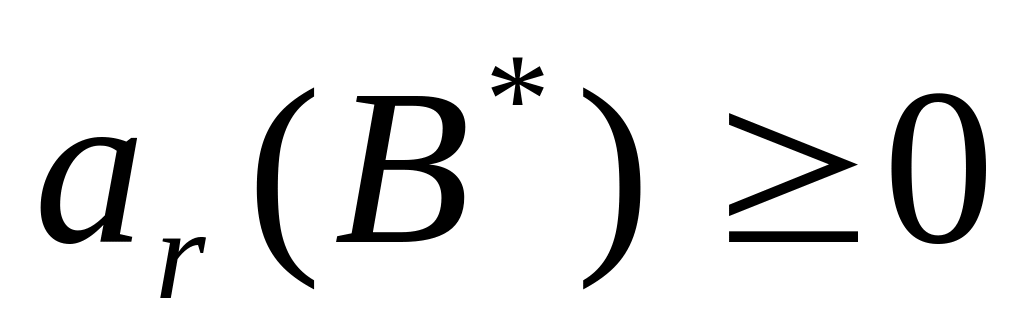 ),
то реализовался выход на образующую
области допустимых решений двойственной
задачи, в направлении которой
),
то реализовался выход на образующую
области допустимых решений двойственной
задачи, в направлении которой
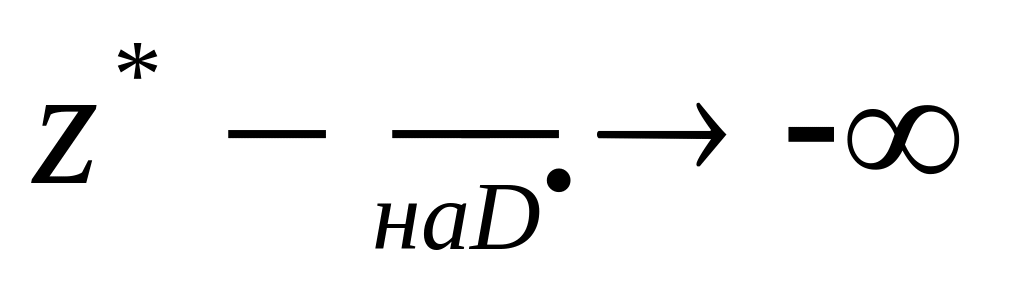 .
Следовательно на основании свойства
1.в
.
.
Следовательно на основании свойства
1.в
.
1.14.3. Алгоритм двойственного симплекс-метода поиска оптимального
решения ЗЛП
На
основе приведенных в 1.14.2 свойств,
определяющих взаимосвязь прямой и
двойственной задач, могут быть
сформулированы двойственные алгоритмы
симплекс-таблиц
![]() или
или
![]() ,
которые отображают правила обычного
алгоритма симплекс-метода применительно
к двойственной ЗЛП на работу со структурой
данных прямой задачи.
,
которые отображают правила обычного
алгоритма симплекс-метода применительно
к двойственной ЗЛП на работу со структурой
данных прямой задачи.
Структура
симплекс-таблиц
и
ничем не отличается от ранее рассмотренных
![]() и
и
![]() .
Преобразования симплекс-таблиц после
определения разрешающего элемента (r
и l)
осуществляются так же, как и ранее.
Отличия проявляются в следующем:
.
Преобразования симплекс-таблиц после
определения разрешающего элемента (r
и l)
осуществляются так же, как и ранее.
Отличия проявляются в следующем:
Алгоритмы двойственного симплекс-метода работают с последовательностью сопряженных базисов
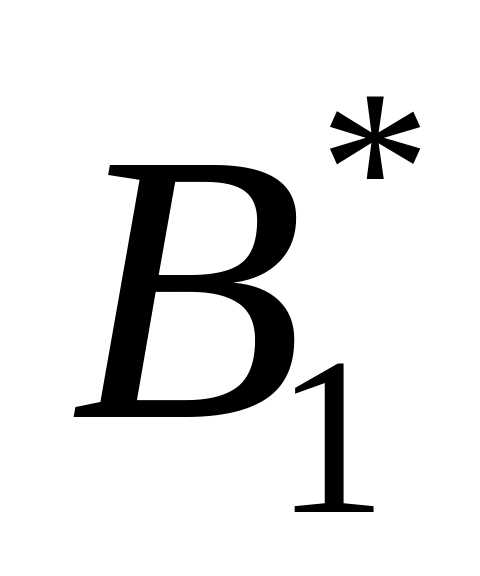 ,
,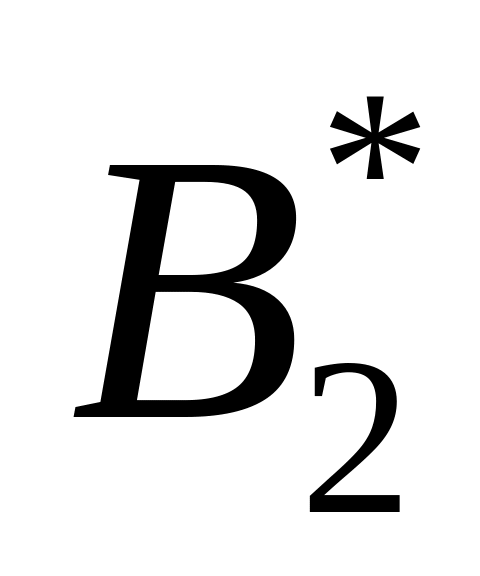 ,…,
,…,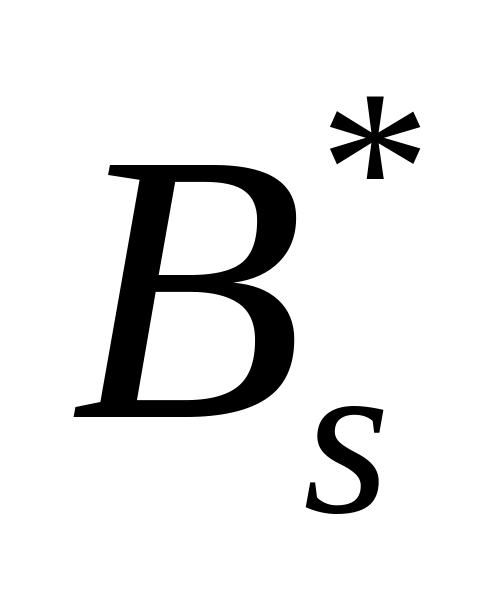 и соответствующих им псевдопланов. В
соответствии со свойствами сопряженного
базиса среди базисных компонент
псевдоплана
и соответствующих им псевдопланов. В
соответствии со свойствами сопряженного
базиса среди базисных компонент
псевдоплана
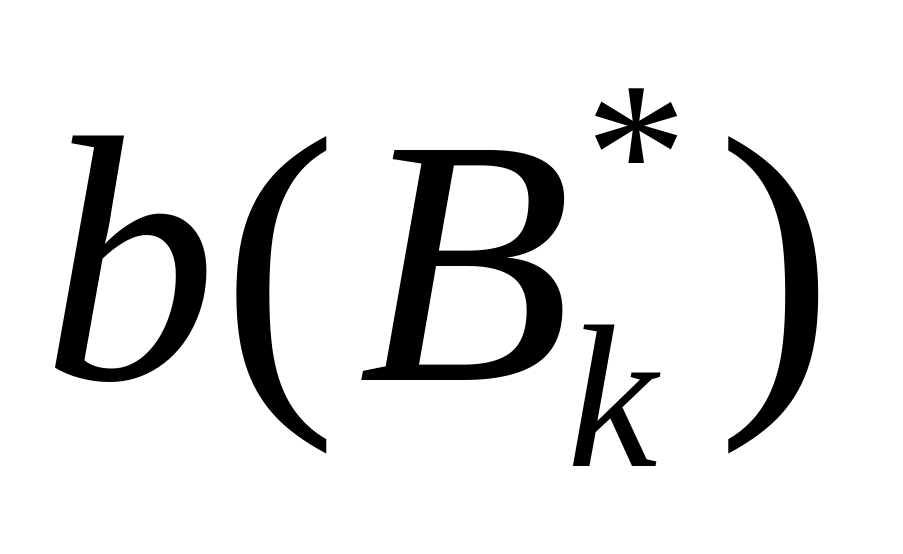 (за исключением
(за исключением
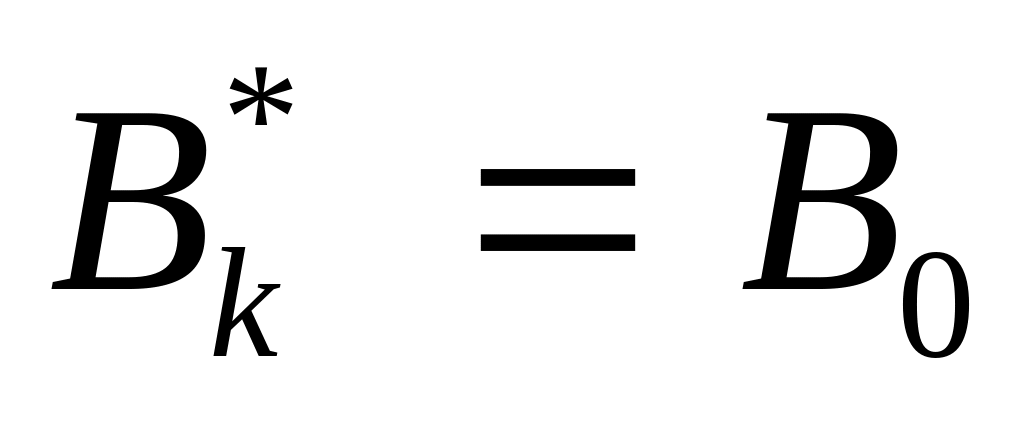 (см. свойство 1.г)) присутствуют
отрицательные элементы (т.е. двойственные
алгоритмы работают, как правило, с
недопустимыми базисными решениями
исходной задачи; в обычном же алгоритме
всегда
(см. свойство 1.г)) присутствуют
отрицательные элементы (т.е. двойственные
алгоритмы работают, как правило, с
недопустимыми базисными решениями
исходной задачи; в обычном же алгоритме
всегда
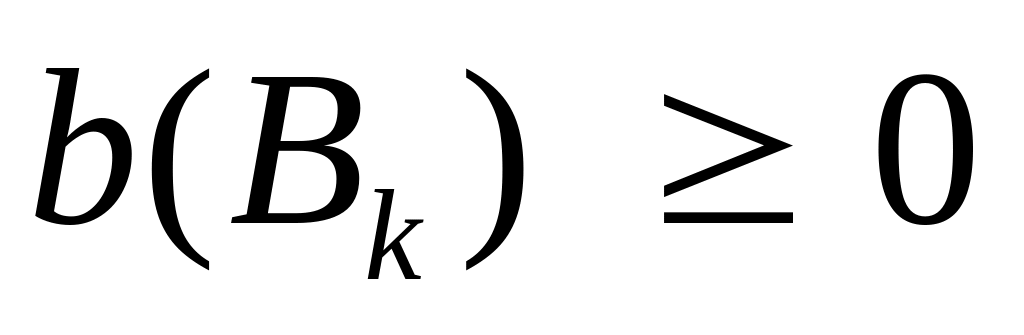 ).
).Симплекс-разности, соответствующие
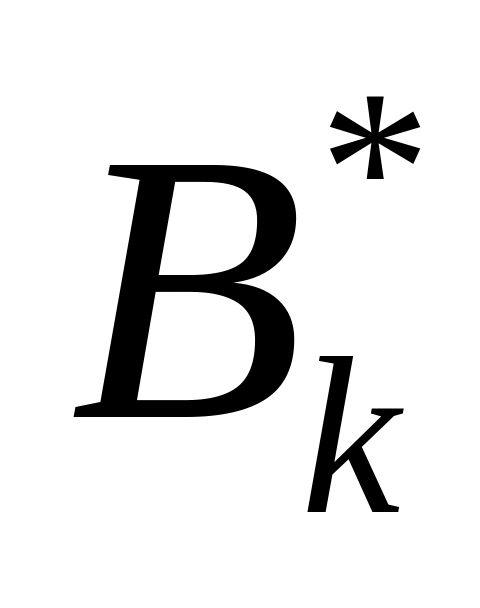 ,
всегда неположительны (
,
всегда неположительны ( - это основной признак сопряженности
базиса, см. свойство 3), в то время как в
обычном алгоритме это свойство
выполняется, лишь когда
- это основной признак сопряженности
базиса, см. свойство 3), в то время как в
обычном алгоритме это свойство
выполняется, лишь когда
 ;
;Основной ожидаемый исход работы алгоритма – нахождения оптимального решения ЗЛП – реализуется в том случае, когда
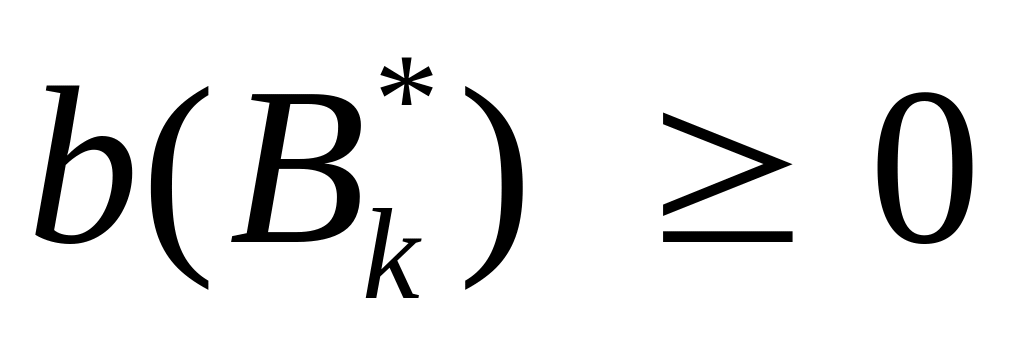 (свойство
1.г), а в обычном алгоритме при выполнении
условия
(свойство
1.г), а в обычном алгоритме при выполнении
условия
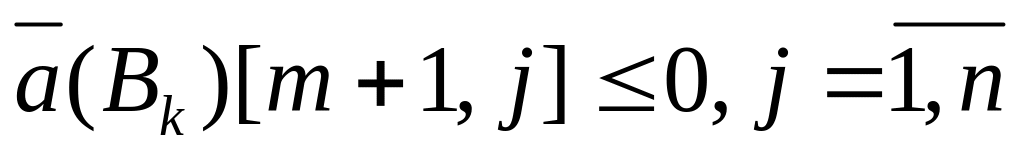 .
.Суть второго возможного исхода работы алгоритма двойственного симплекс-метода относительно решаемой прямой задачи является кардинально другим: , если выполняются условия свойства 4 (при работе обычного симплекс-метода второй возможный исход )
Изменяется порядок выбора разрешающего элемента: вначале на основе свойства 4 выбирается разрешающая строка r, а затем на основе (1.105, 1.106) выбирается разрешающий столбец l.
Для выбора r можно использовать следующие формальные соотношения:
![]() , (1.108)
, (1.108)
где
![]() . (1.109)
. (1.109)
В приводимом ниже алгоритме для краткости совместим изложение вариантов и , помещая в {…} дополнительные вычислительные операции, требуемые алгоритмом .
Алгоритм двойственного симплекс-метода.
Шаг 1. k=1.
Шаг
2. Проверка условия оптимальности
псевдоплана (![]() ).
Если оно выполнятся, то
).
Если оно выполнятся, то
- выписывается оптимальное решение,
- алгоритм завершает свою работу.
Шаг 3. Выбор номера разрешающей строки r (1.108, 1.109).
Шаг
4. Проверка условия
![]() Æ.
Æ.
{Расчет
разрешающей строки матрицы
![]() :
:
![]() }
(1.110)
}
(1.110)
Если
условие (![]() )ÞD=Æ
выполняется, то алгоритм завершает свою
работу.
)ÞD=Æ
выполняется, то алгоритм завершает свою
работу.
Шаг 5. Выбор номера разрешающего столбца l.
{Расчет строки симплекс-разностей (1.89).}
Реализация соотношений 1.105 и 1.106.
Шаг 6. Преобразование симплекс-таблицы относительно разрешаемого элемента:
Преобразование базисного множества;
{ Расчет разрешающего столбца.} Преобразование действительной части симплекс-таблицы относительно разрешающего элемента.
Комментируя
работу алгоритма, необходимо отметить,
что при переходе от итерации k
к k+1
значение целевой функции
![]() не будет возрастать, а при
не будет возрастать, а при
![]() будет уменьшаться.
будет уменьшаться.
И
еще одно замечание. При использовании
(ручной
счет) в отличие от структуры данных,
показанной на рис. 1.21 используется
структура данных, показанная на рис.1.25:
строки матрицы
![]() на большинстве итераций алгоритма (за
исключением случая
)
рассчитываются парами.
на большинстве итераций алгоритма (за
исключением случая
)
рассчитываются парами.
