Санкт-Петербургский государственный морской технический университет

Курсовая работа

«Исследование и расчёт электромеханической

следящей системы»

Выполнил:

Студент гр. 33РК1

Васекина Ю.В

Проверил:

Шереметов Б.Б

Санкт-Петербург

2005

Оглавление:

1.Исходные данные------------------------------------- стр.3

2.Задание к курсовому проекту------------------------- стр.3

3.Определение Характеристики

детерминированного сигнала:

a.Спектральные характеристики S(), S(), ().--- стр.4

b. Корреляционную функцию сигнала К().-------------- стр.6

4. Определение характеристик линейной цепи.

1. Частотные характеристики К() , К(),_к().---- стр.7

b.Временные характеристики g(t), h(t). ------------ стр.9

5. Определение токов и напряжений на всех

элементах схемы при подаче на

вход заданного детерминированного сигнала.------- стр.11

6. Определение К_вых(),G_вых(). Нахождение

интервала корреляции _к , и аналитической

ширины спектра _э.-------------------------------- стр.17

7.Эксперементальные данные---------------------------- стр.19

Исходные данные :

1. Детерминированный сигнал.

2. Схема линейной цепи.

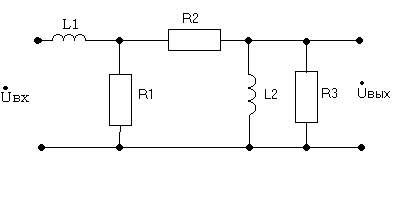
Требуется определить :

1.Характеристики детерминированного сигнала:

a.Спектральные характеристики S(), S(), ().

B.Корреляционную функцию сигнала К().

2.Определить характеристики линейной цепи.

a.Частотные характеристики К() , К(),_к().

b.Временные характеристики g(t), h(t).

3.Определить токи и напряжения на всех элементах схемы при подаче на вход заданного детерминированного сигнала.

4.Определить К_вых(),G_вых().Найти интервал корреляции _к , и аналитическую ширину спектра _э.

1.Определение характеристик детерминированного сигнала.

1.A Спектральная плотность.

Спектральная плотность импульсного (непериодического) сигнала s(t) определяется с помощью интегрального преобразования Фурье

где

Графически спектральная плотность характеризуется зависимостью от частоты ее модуля и аргумента

Так как сигнал чётный, то , а В()=0. Записывая детерминированный сигнал аналитически получим :

s(t)=E/2(1+cos₀t), при - t  

Подставляя в интегральное преобразование Фурье получим:

вычисляя это выражение получим :

графики модуля спектральной плотности и аргумента представлены на рис.1 и рис.2 соответственно.

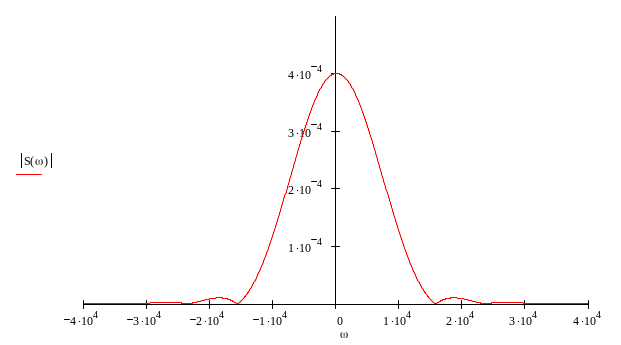
рис.1

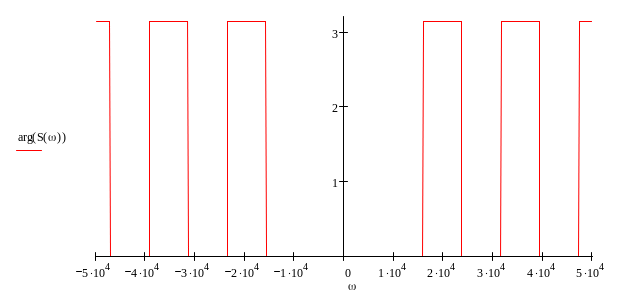
рис.2