3.3.2. Эйлеровы и гамильтоновы пути и циклы

Эйлеров путь (цикл) в графе – это путь (цикл), проходящий все рёбра графа по одному разу. Гамильтонов путь (цикл) – это простой путь (цикл), обходящий все вершины графа.

Конечно, эйлеров (или гамильтонов) путь или цикл существует далеко не во всяком графе. Обязательное требование на граф для существования эйлерова (гамильтонова) пути/цикла – это связность графа. Но этого, вообще говоря, недостаточно. Необходимые и достаточные условия существования эйлерова пути/цикла даёт следующая теорема.

Теорема. Пусть – связный граф. Тогда:

1. эйлеров путь (незамкнутый) в существует в том и только том случае, если в точности две вершины имеют нечётные степени, а остальные – чётные;

2. эйлеров цикл в существует в том и только том случае, если все вершины имеют чётные степени.

Замечания. 1. Данная теорема верна и для графов с кратными рёбрами. Наличие или отсутствие петель в графе не имеет значения.

2. Если в точности две вершины, скажем, и имеют нечётные степени, то эйлеров путь, хотя и определяется неоднозначно, но обязательно должен иметь вершины и своими концами.

Гамильтоновы пути/циклы имеют большое практическое значение. Например, если граф представляет собой сеть дорог, по которым может ходить курьер, то для обхода всех вершин графа курьеру следует идти по гамильтонову пути (если, конечно, такой путь существует). Ещё более сложной, чем нахождение какого-нибудь гамильтонова пути, является задача нахождения кратчайшего гамильтонова пути. С вычислительной точки зрения эти задачи (установить, существует ли гамильтонов путь, найти все гамильтоновы пути, найти кратчайший гамильтонов путь) являются сложными и требуют большого количества операций. В отличие от них, существует простой алгоритм нахождения эйлерова пути или цикла. Сформулируем его.

Алгоритм построения элерова пути/цикла. Пусть – связный граф и выполнены условия теоремы (т.е. либо все вершины чётной степени, либо ровно две имеют нечётную степень. Если все вершины чётные, то построение пути начинаем с любой вершины, а если две вершины нечётные, то начинаем именно с нечётной вершины. Пусть в качестве начала пути выбрана вершина Тогда мы идём из этой вершины в любую другую и убираем ребро, по которому только что прошли. Попав в следующую вершину, мы идём дальше и убираем только что пройденное ребро. И т.д. Надо только следить за тем, чтобы ребро, по которому мы хотим пройти, не было перешейком (перешейком называется ребро, удаление которого из графа нарушает связность – см. рис. 3.27). Можно доказать, что при реализации алгоритма, если все рёбер, исходящих из текущей вершины, являются перешейками, то (т.е. данная вершина – висячая). В этом случае мы идём по этому ребру и удаляем не только ребро, но и вершину, из которой только что шли по этому ребру. В конце концов мы придём во вторую нечётную вершину (если ровно две вершины графа были нечётные) или в начальную вершину пути (если все вершины были чётные).

Упражнение 3.22. Выяснить, имеет ли граф, изображённый на рисунке 3.28а, эйлеров путь или цикл, и если имеет, то построить его.

Р ешение. Напишем на каждой вершине графа степень вершины (см. рис. 3.28б). Так как ровно две вершины имеют нечётные степени (это вершины и ), то существует эйлеров путь, и он идёт из вершины в вершину или наоборот. Начнём путь с вершины и применим алгоритм. Тогда получим путь

Отметим, что наличие у графа эйлерова пути или цикла означает возможность нарисовать граф, не отрывая карандаша от бумаги.

Упражнение 3.23. Выяснить, существует ли гамильтонов путь или цикл в графе, изображённом на рисунке 3.29.

Р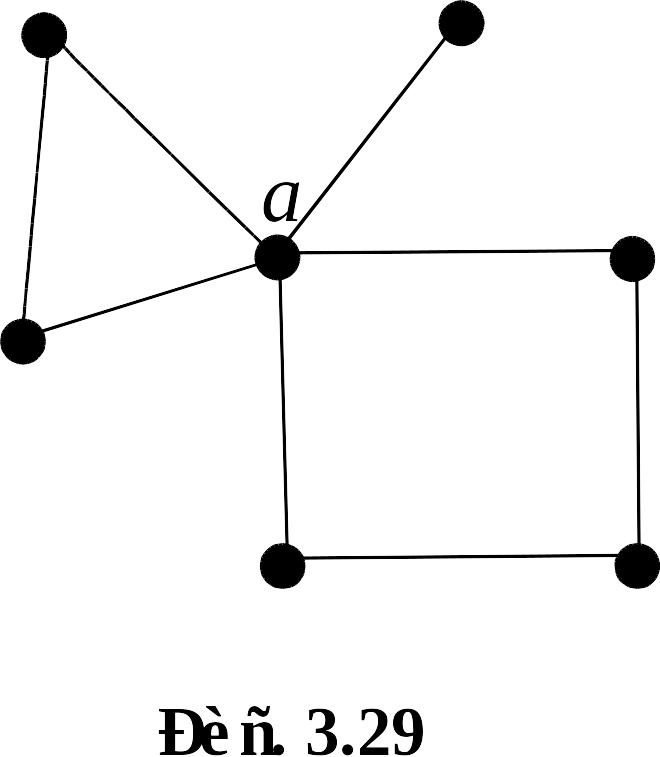 ешение. Заметим, что если в графе есть вершина, после удаления которой граф распадается на 3 или более компонент связности, то у него не может быть гамильтонова пути или цикла. Действительно, пусть вершина с вышеуказанным свойством существует. Обозначим её через Если бы в графе гамильтонов путь (или цикл) существовал, то по этому пути (или циклу) мы проходили бы через вершину более одного раза, что противоречит определениям. В графе на рисунке 3.29 такая точка есть. Значит, у него нет гамильтонова пути или цикла.