23. Теорема о тензорном произведении мер.
Определение.
Пусть
-
мера на полукольце
,
-
мера на полукольце
и
-полукольцо.
Определим на полукольце S
- меру
,
где
,
.
Тогда
-
называется тензорным
произведением
и
и записывается следующим образом:
.
Теорема (о тензорном произведении мер).
Тензорным
произведение мер является мерой, т.е.
если
-
мера на пространстве
,
а
-
мера на пространстве
,
то
является мерой на пространстве
.
Доказательство.
I.
Возьмем
-полукольца
множеств на пространствах
соответственно. Тогда
представляется в виде:
,
где
,
тогда
.
II.
Докажем, что если
,
где
,
тогда
-
это свойство аддитивности меры
.
Для этого рассмотрим характеристическую функцию
(1)
Т.к.
,
где
,
тогда
(2)
Аналогично,
,
где
,
тогда
(3)
Поскольку
,
то
(4)
Подставляем (2), (3), (4) в (1):
(5)
Т.к. характеристическая
функция множеств является интегрируемой,
то можно проинтегрировать равенство
по
:
Получаем:
(6)
Полученное
соотношение (6) проинтегрируем по
множеству
:
Получаем:
Из этого по определению следует: .
Таким образом, доказали аддитивность .
Итак, - неотрицательна и аддитивна, значит является мерой.
24. Двойные и повторн инт от тенз произв. Т.Фубини и Тонелли.
Интеграл от функции
называется интегралом Лебега:
,
иногда пишут
.
Будем рассматривать интегралы
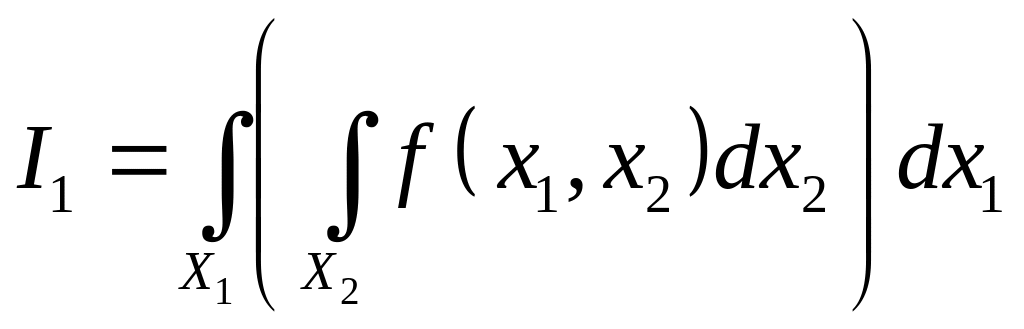и
.
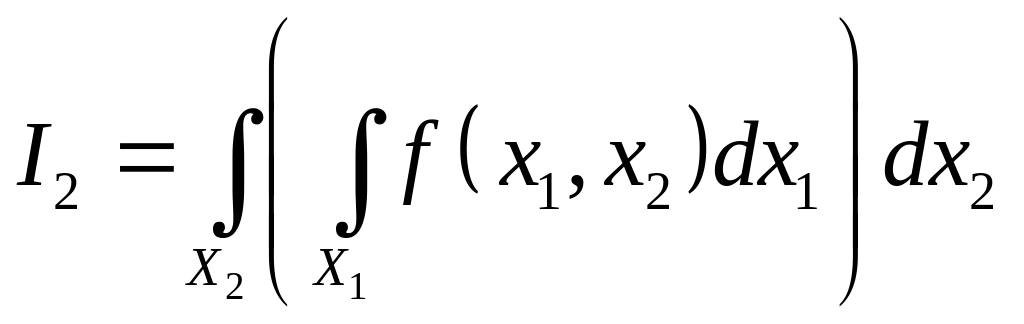Эти интегралы называют повторными.
Теорема Фубини.(о связи между двойным интегралом и повторными интегралами)
Если функция
интегрируема по тензорному произведению
мер
,
т.е. существует интеграл
.Тогда
существуют повторные интегралы:
и
и имеет место рав-во
= + . Обратное неверно.
Теорема Тонелли.
Если функция
измерима по мере
и существует хотя бы один из повторных
интегралов
,
тогда функция
интегрируема по мере
и существует двойной интеграл, причем
он равен повторным.
25.Опр-е векторного пр-ва. Алгебр. операции над мн-вами.
Пусть
– поле действительных чисел
или поле комплексных чисел
и будем рассматривать векторные
пространства над этим полем. Это значит,
будем рассматривать:
1)
;
2) операцией умножения
называется произведение числа на элемент , при этом должны выполняться некоторые свойства:
1. - коммутативная группа относительно сложения.
а) ассоциативность:
,
существует нейтральный элемент, т.е.
существует обратный элемент, т.е.
коммутативность:
,
2. Аксиома дистрибутивности.
a)
b)
c)
3. Условие нормировки.
Алгебр операции над мн-вами
Если
и
-
два подмножества из векторного
пространства
,
т.е.
,
то определим
.
Если одно из этих
множеств является одноточечным, например
,
то будем писать
.
Соответственно, если
,
то
.
Аналогично для
умножения. Пусть
.
Определим подмножество
Если -одноточечное,
т.е.
,
то будем писать
,
а если
,
то
.
Пример 1. Рассмотрим
множества
и
.
Тогда
– открытая правая полуплоскость.
Пример 2.
Пусть
,
тогда
,
а
,
следовательно,
.