
- •1.Метрические пр-ва. Шары, открытые и закрытые мн-ва.
- •7.Непрерывн. Отобр., св-ва.
- •8.Сжимающие отобр-я, св-ва
- •9. Принцип неподвижной точки
- •10.Полукольца мн-в и мера на полукольцах. Св-ва
- •11.Кольца мн-в и их св-ва
- •12.Теорема о распространении мера с полукольца на кольцо
- •13.Примеры мер, опр-ных на всех мн-вах
- •14.Внешняя мера и ее св-ва
- •15.Ступенчатые ф-ции
- •16.Интеграл от ступенчатой ф-ции
- •17.Интеграл от интегрируемой ступенчатой ф-ции
- •18.Измеримые ф-ции и их св-ва
- •19.Сходимость почти всюду. Канторово мн-во.
- •20.Интегрируемые ф-ции. Интеграл Лебега.
- •22.Тензорное произведение мер
- •23. Теорема о тензорном произведении мер.
- •24. Двойные и повторн инт от тенз произв. Т.Фубини и Тонелли.
- •26.Векторные подпр-ва и фактор пр-ва
- •28.Порождающие мн-ва. Базисы. Теорема о сущ алг базиса.
- •29.Линейный оператор. Св-ва.
- •30.Линейные функционалы. Теорема Хана-Банаха.
20.Интегрируемые ф-ции. Интеграл Лебега.
Определение.
Функция
называется интегрируемой (по Лебегу),
если существует последовательность
![]() интегрируемых ступенчатых функций,
которые равномерно сходятся к функции
:
на
.
интегрируемых ступенчатых функций,
которые равномерно сходятся к функции
:
на
.
Совокупность всех
интегрируемых функций обозначается
![]() .
.
Свойства интегрируемых функций.
1.![]() ,
,
![]() :
:
![]() .
.
2.
![]()
,
![]() на
.
на
.
3.
![]() ,
то есть
,
то есть
![]() .
.
4.
![]()
Определение. Интегралом Лебега от интегрируемой функции называется число, обозначаемое
![]() (1)
(1)
где
![]() - последовательность ступенчатых
интегрируемых функций, равномерно
сходящихся к функции
- последовательность ступенчатых
интегрируемых функций, равномерно
сходящихся к функции
![]() .
.
Для доказательства
корректности определения интеграла
нужно доказать, что существует предел
![]()
Обозначим
![]() .
Необходимо доказать, что
.
Необходимо доказать, что
![]() - фундаментальная последовательность.
- фундаментальная последовательность.
![]()
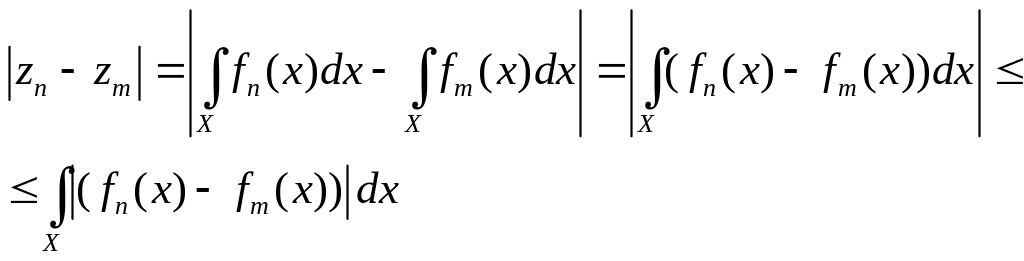 (2)
(2)
![]() .
Тогда из (2) получим
.
Тогда из (2) получим
![]() ,
,
![]() .
Таким образом,
.
Таким образом,
![]() .
.
Это означает, что если последовательность фундаментальная.
Так как полно, то последовательность сходится, следовательно, существует и он конечен, значит определение корректно.
21.Св-ва интеграла лебега
Свойства интеграла Лебега.
1. .
Д-во:
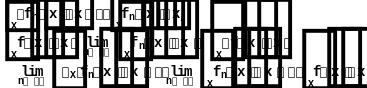
2.
![]() .
.
Д-во. Берем
![]() .
Для них верно
.
Для них верно
 ,а значит 2 док-но.
,а значит 2 док-но.
3. Линейность.
![]() .
.
4. .
![]()
5.
Если f g
, т.е. они равны друг другу почти всюду,
и существует
![]() ,
то
,
то
![]() также существует, причем
также существует, причем
![]() .
.
Если f g , т.е.
существует
![]() .
Тогда
.
Тогда
![]()
![]()
![]()
![]()
![]() .
.
![]() ,
т.к. интеграл по множеству меры 0 равен
0.
,
т.к. интеграл по множеству меры 0 равен
0.
Отношение называется отношением эквивалентности, если оно удовлетворяет :
f f(рефлексивность);
f g gf (симметричность)
f g ,gh fh (транзитивность)
Проверим выполнение условие 3).
f g , это значит,
![]()
gh , это означает,
![]()
![]() ,т.е.
,т.е.
![]()
Отметим, что
![]() измеримо,т.к. сумма двух измеримых мн-в
образует алгебру.
измеримо,т.к. сумма двух измеримых мн-в
образует алгебру.
Поэтому в силу f(x)=g(x) и g(x)=h(x) следует f(x)=h(x).
Совокупность пространств по эквивалентности
называется фактор-пространством
![]() .
Будем называть пр-вом интегрируемых
ф-ций на мн-ве Х.
.
Будем называть пр-вом интегрируемых
ф-ций на мн-ве Х.
22.Тензорное произведение мер
Напомним, что если
есть две функции
и
![]() ,
то можно построить тензорное произведение
этих функций:
,
то можно построить тензорное произведение
этих функций:
![]() .
.
Операция называется тензорным произведением.
Определим векторное произведение :
![]() .Аналогично
для
.Аналогично
для
![]() .
.
В пр-ве
![]() рассмотрим пулокольцо мн-в
рассмотрим пулокольцо мн-в
![]() ,
а в пр-ве
,
а в пр-ве
![]() -
-
![]() .
.
Определим
![]() -
прямое произведение полуколец
-
прямое произведение полуколец
![]() и
и
![]() .
.
Теорема (о прямом произведении полуколец).
Прямое произведение полуколец является полукольцом.
Доказательство.
Пусть
-
полукольцо подмножеств множества
![]() ,
,
-
полукольцо подмножеств множества
![]()
Пусть
![]() -
прямое произведение.
-
прямое произведение.
Докажем, что S
является полукольцом подмножеств
множества
![]() .
.
I.
Пусть
![]() .
Докажем, что
.
Докажем, что
![]() .
.
Т.к.
![]() ,
то можем записать
,
то можем записать
![]() .
.
Аналогично
![]() ,
где
,
где
![]() ,
,
![]() .
.
Имеем
![]() .
.
Т.к.
- полукольцо, то
![]()
Т.к.
![]() -
полукольцо, то
-
полукольцо, то
![]()
Тогда
![]() .
.
II.
Пусть
![]()
![]() ,
где
,
и
,
где
,
и
![]() ,
тогда
,
тогда
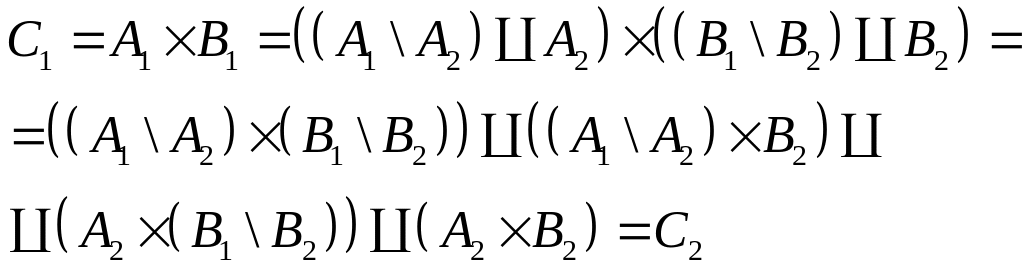
Получаем, что
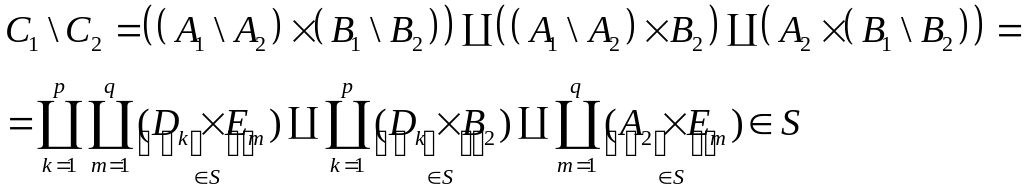 В
последних равенствах
В
последних равенствах
![]() ,
,
![]() т.к.
т.к.
![]() .
.
Следовательно, S является полукольцом.
