9. Принцип неподвижной точки

Теорема (принцип неподвижной точки).

Пусть – сжимающее отображение полного метрического пространства , тогда существует единственная неподвижная точка у отображения .

Доказательство.

Возьмем произвольную точку и построим точку . По точке строим точку

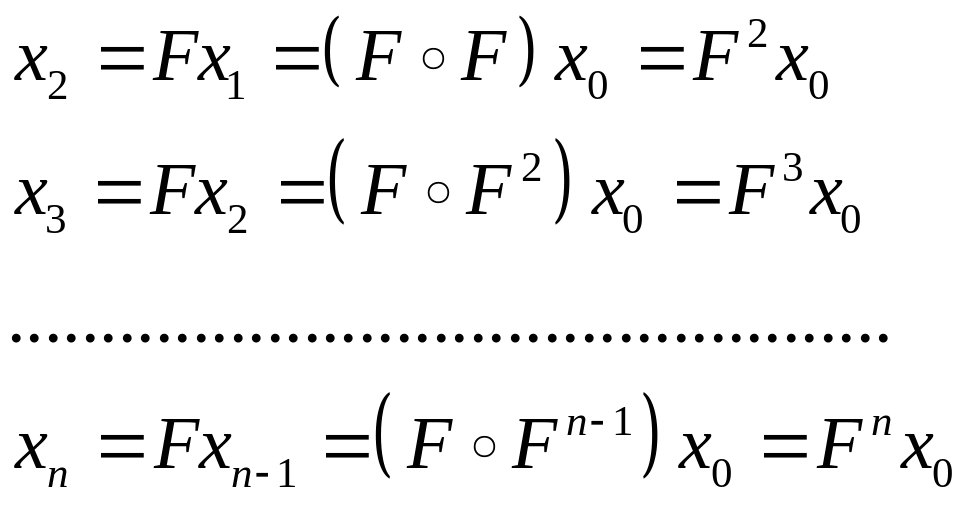
Получили последовательность .

Докажем, что эта последовательность фундаментальна.

Возьмем числа ,будем считать, что , тогда запишем .

Рассмотрим расстояние

, т.к. отображение сжимающее, то , значит

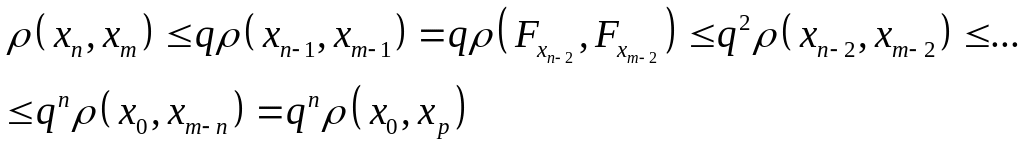
Таким образом, доказали неравенство

(3)

Рассмотрим и применим неравенство треугольника:

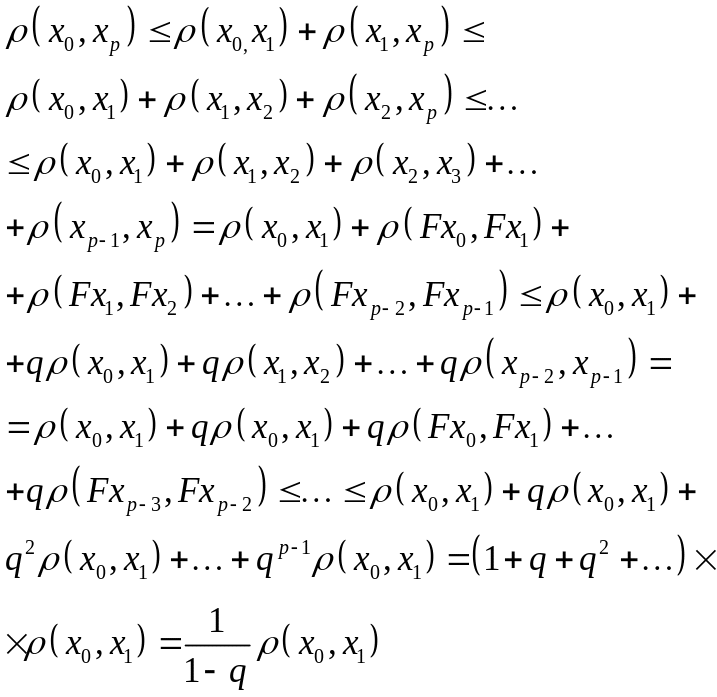
Таким образом, доказали неравенство:

(4)

Из (3) и (4) получаем

(5)

Рассмотрим правую часть (5). Так как , то , следовательно, вся правая часть .

Это значит, что

(6)

Т.к. , то соотношение (6) верно и для .

Таким образом, получаем:

А эта формула означает, что последовательность является фундаментальной последовательностью в метрическом пространстве . В силу условия теоремы о том, что метрическое пространство полное, получаем, что последовательность является сходящейся последовательностью, т.е. существует такой элемент .

Рассмотрим равенство

, которое верно для (7)

Исследуем левую часть (7): , исследуем правую часть (7): . Т.к. отображение по условию теоремы сжимающее, то оно непрерывно и, следовательно, применяя теорему об эквивалентном условии непрерывности, получаем .

Переходя в общих частях равенства (6) к пределу при , получаем в пределе , т.е. - неподвижная точка отображение .

Таким образом, доказали, конструктивно построив, существование неподвижной точки. Единственность неподвижной точки следует из доказанной выше теоремы.

Замечание.

Из неравенства (5), доказанного в теореме, можем получить скорость приближения построенных итераций к неподвижной точке.

Действительно, переходя в (5) к пределу при , и учитывая, что , получаем

(8)

10.Полукольца мн-в и мера на полукольцах. Св-ва

Пусть имеем множество . Его подмножества будем обозначать Пустое подмножество множества обозначим . Совокупность всех подмножеств множества : .

Элементы множества называются точками.

А также на введены операции :

Объединение:

Пересечение:

Разность:

Дополнение:

Симметрическая разность:

.

Свойства:

1. дистрибутивность;

2. ассоциативность;

3. коммутативность.

Семейство мн-в наз-ся непересекающимися, если любые взятые из этого семейства мн-ва попарно не пересекаются.

Определение. Система подмножеств S множества , которая содержится в , называется полукольцом, если:

1)

2)

Примеры полуколец.

1. Пусть X =R и 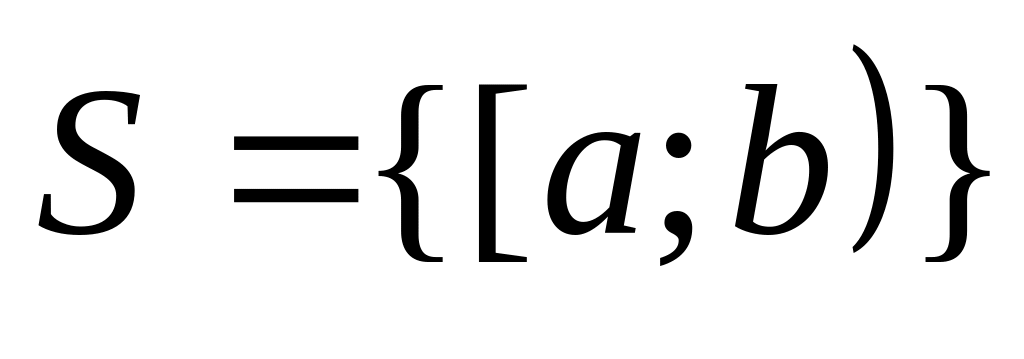. Пересечение полуинтервалов – полуинтервал. Множество полуинтервалов образуют полукольцо.

2. Пусть и 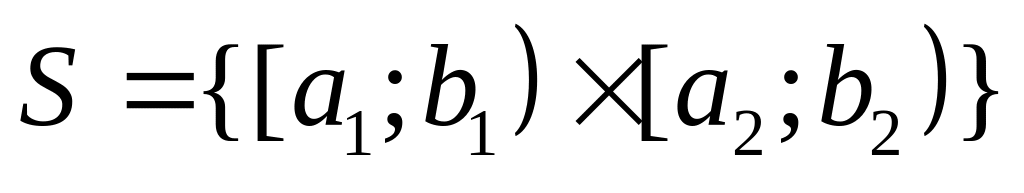- двумерная ячейка.

3. Пусть и 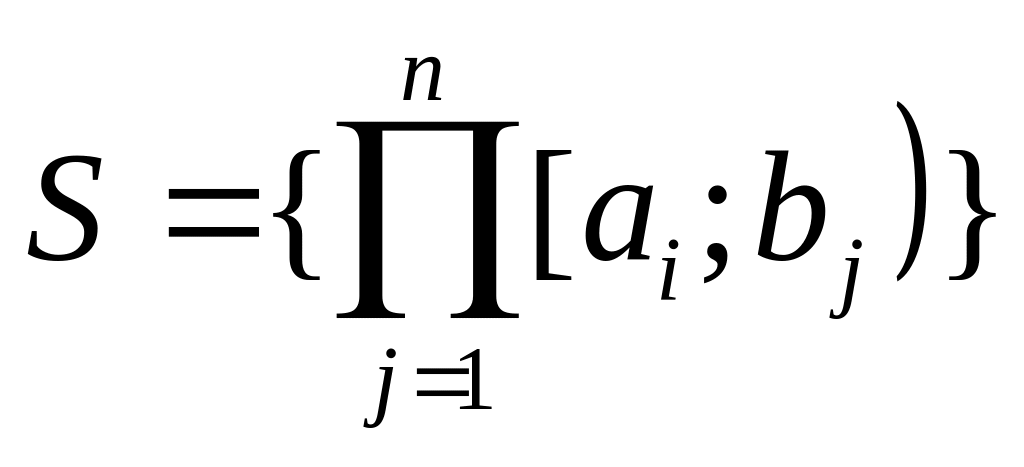- -мерная ячейка.

4. 

Пусть P-полукольцо мн-в . Говорят, что на P задана мера , если AP этому мн-ву А сопоставлено число (A)0, причем выполняются сл условия: 1)

2) --св-во аддитивности.

Это понятие объединяет площади, длины и т.д.

Возьмем в качестве Р пример 4

1)([a;b))=b-a -длина

2)возьмем полукольцо из примера 5.

--получили площадь.

3) возьмем полукольцо из примера 6

Св-ва меры:

1)

Действительно (3)

из (3) .

2) Монотонность меры.

Очевидно, т.к.

Применим аддитивность: