
- •Лекции по курсу: «численные методы»
- •Приближение функций
- •Численное интегрирование
- •Квадратурные формулы Ньютона-Котеса
- •Частные случаи формул Ньютона-Котеса
- •Квадратурные формулы наивысшей алгебраической степени точности (н.А.С.Т.)
- •Квадратурная формула Гаусса (частный случай квадратурной формулы н.А.С.Т. При )
- •Смысл введения весовой функции
- •Приближённое решение алгебраических и трансцендентных уравнений
- •Методы решения систем линейных алгебраических уравнений (слау)
- •Приближённое решение проблемы собственных значений матрицы
Смысл введения весовой функции
Пусть требуется
вычислить
![]() (1).
(1).
при численном
интегрировании чаще всего подынтегральная
функция
заменяется алгебраическим многочленом
(в частности интерполяционным). Для того
чтоб такая замена имела хорошую точность,
функция
должна обладать высокой степенью
гладкости (должна обладать достаточным
количеством непрерывных производных),
если же
имеет особенности на
(разрывы, обращается в бесконечность в
одной или нескольких точках отрезка),
то применение квадратурной формулы
вида
![]() будет давать большую погрешность,
поскольку такие функции плохо приближаются
алгебраическими многочленами.
будет давать большую погрешность,
поскольку такие функции плохо приближаются
алгебраическими многочленами.
Для избегания больших
погрешностей исходную функцию
представляют в виде:
![]() ,
где
содержит все особенности функции
,
называется весовой функцией, а
является гладкой. И тогда применение к
интегралу (1)
квадратурной формулы
не даёт такую большую погрешность.
,
где
содержит все особенности функции
,
называется весовой функцией, а
является гладкой. И тогда применение к
интегралу (1)
квадратурной формулы
не даёт такую большую погрешность.
Описанный метод называется методом выделения особенностей.
Пример.
Пусть надо
вычислить интеграл
![]() ,
где
,
где
![]() имеет особенности в точках
и
имеет особенности в точках
и
![]() .
Представим
в следующем виде:
.
Представим
в следующем виде:
![]() ,
где
,
где
![]() - весовая функция,
- весовая функция,
![]() .
Тогда
.
Тогда
![]() .
.
{ Самостоятельно законспектировать тему: «Приближённое вычисление кратных интегралов»}
Приближённое решение алгебраических и трансцендентных уравнений
Постановка задачи
Пусть задано нелинейное
уравнение
![]() (1),
где
-
функция определённая и непрерывная на
некотором конечном или бесконечном
интервале
(1),
где
-
функция определённая и непрерывная на
некотором конечном или бесконечном
интервале
![]() .
Если
.
Если
![]() ,
где
,
где
![]() -
комплексные коэффициенты, причём
-
комплексные коэффициенты, причём
![]() ,
то уравнение (1)
называется алгебраическим уравнением
-й
степени.
,
то уравнение (1)
называется алгебраическим уравнением
-й
степени.
Во всех остальных случаях, когда не полином, уравнение (1) называется трансцендентным.
Определение.
Всякое значение
![]() обращающее функцию
в ноль, то есть такое, что
обращающее функцию
в ноль, то есть такое, что
![]() называется нулём функции
или корнем уравнения (1).
называется нулём функции
или корнем уравнения (1).
Корень
![]() называется изолированным корнем
уравнения (1),
если существует окрестность корня
не содержащая других корней уравнения
(1).
называется изолированным корнем
уравнения (1),
если существует окрестность корня
не содержащая других корней уравнения
(1).
В дальнейшем будем считать все корни уравнения (1) изолированными.
Если уравнение (1) алгебраическое или трансцендентное имеет достаточно сложный вид, то его сравнительно редко удаётся решить точно, поэтому важное значение принимают приближённые методы решения уравнения (1), а также оценка степени их точности.
Приближенное нахождение корней нелинейного уравнения (1) разбивается на два этапа:
отделение корней, то есть установление по возможности тесных промежутков
 содержащих один и только один корень
уравнения (1);
содержащих один и только один корень
уравнения (1);уточнение корней – доведение их до нужной степени точности.
Методы отделения корней
Методы отделения корней делятся на две группы:
аналитические;
графические.
Графические методы отделения корней
Известно, что действительные корни уравнения геометрически являются абсциссой точек пересечения графика функций
 с осью
с осью
 ,
то есть те значения
при которых
,
то есть те значения
при которых
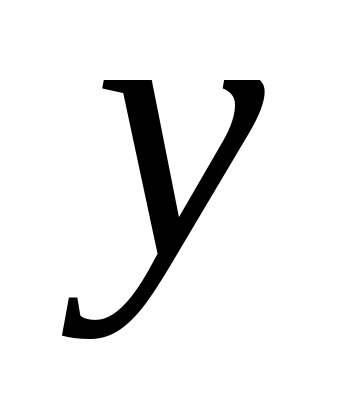 обращается в ноль.
обращается в ноль.

Если уравнение (1) не содержит близких между собой корней, то таким образом они легко отделяются.
Если функция сложная, но представима в виде разности:
 ,
где
и
,
где
и
 более простые, чем
,
то тогда на практике бывает выгодно
уравнение
заменить на эквивалентное
более простые, чем
,
то тогда на практике бывает выгодно
уравнение
заменить на эквивалентное
 (два
уравнения называются эквивалентными,
если имеют одинаковые корни). Тогда
корни уравнения
получаются как абсциссы точек пересечения
графиков функций
(два
уравнения называются эквивалентными,
если имеют одинаковые корни). Тогда
корни уравнения
получаются как абсциссы точек пересечения
графиков функций
 и
и
 .
.

Заметим, что, несмотря на свою простоту, графические методы пригодны лишь для грубого отделения корней.
Аналитические методы отделения корней
Первый из методов основан на применении известной теоремы математического анализа, теоремы Больцано-Коши: если непрерывная функция на концах отрезка принимает значения разных знаков, то есть
 ,
то на отрезке
содержится по меньшей мере один
действительный корень уравнения
.
,
то на отрезке
содержится по меньшей мере один
действительный корень уравнения
.
Замечание.
Корень уравнения (1)
заведомо будет единственным на
,
если
монотонна на этом отрезке, либо же
производная
![]() существует и сохраняет постоянный знак
на
.
существует и сохраняет постоянный знак
на
.
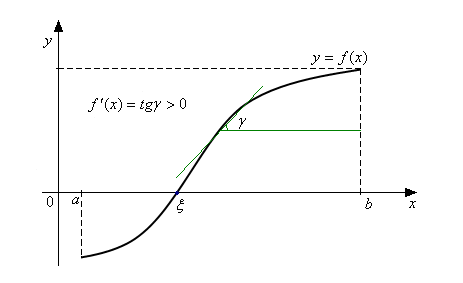
Если заранее известно
количество
действительных корней уравнения
(1),
то на практике часто бывает достаточно
провести процесс половинного деления
для аналитического отделения корней
данного уравнения (1).
С этой целью отрезок
разбивают последовательно на
![]() частей и определяют знаки функции
в точках деления. Если для функции
будет получено ровно
перемен знака, то таким образом все
корни будут отделены.
частей и определяют знаки функции
в точках деления. Если для функции
будет получено ровно
перемен знака, то таким образом все
корни будут отделены.
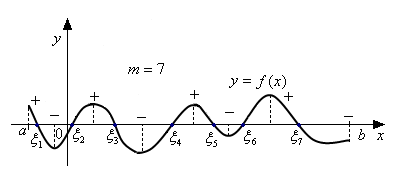
В данном случае получили 7 перемен знака, таким образом все корни отделены.
Пусть уравнение (1)
является алгебраическим уравнением
-й
степени, то есть
,
![]() (2).
(2).
Основная теорема алгебры (теорема Гаусса). Алгебраическое уравнение -й степени имеет ровно корней, действительных или комплексных, причём каждый корень считается столько раз какова его кратность.
Теорема 1.
Если все коэффициенты уравнения (2)
![]() вещественные числа, то комплексные
корни такого уравнения будут попарно
комплексно-сопряжённые, то есть если
вещественные числа, то комплексные
корни такого уравнения будут попарно
комплексно-сопряжённые, то есть если
![]() - корень уравнения (2)
кратности
- корень уравнения (2)
кратности
![]() ,
то
,
то
![]() так же является корнем уравнения (2)
той же кратности
.
так же является корнем уравнения (2)
той же кратности
.
Следствие. Алгебраическое уравнение (2) нечётной степени с действительными коэффициентами имеет, по меньшей мере, один действительный корень.
Дадим оценку модулей всех корней уравнения (2), то есть укажем границы нахождения корней этого уравнения.
Теорема 2.
Пусть
![]() ,
,
![]() ,
где
,
где
![]() - коэффициенты уравнения (2),
тогда для абсолютных значений корней
уравнения (2)
имеет место следующая оценка:
- коэффициенты уравнения (2),
тогда для абсолютных значений корней
уравнения (2)
имеет место следующая оценка:
![]() .
.
Замечание.
Из теоремы 2 следует, что все корни
уравнения (2)
расположены
в круге радиуса
![]() .
Действительные корни
расположении на оси абсцисс в интервале
.
Действительные корни
расположении на оси абсцисс в интервале
![]() .
.
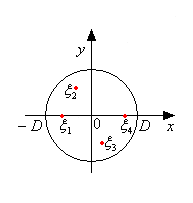
Если известны границы интервала, содержащие все действительные корни уравнения (2), то естественно возникает вопрос об их количестве. Ответ на этот вопрос даёт теорема Штурма.
Пусть задано нелинейное алгебраическое уравнение вида (2). Системой Штурма полинома -й степени называется следующая совокупность функций
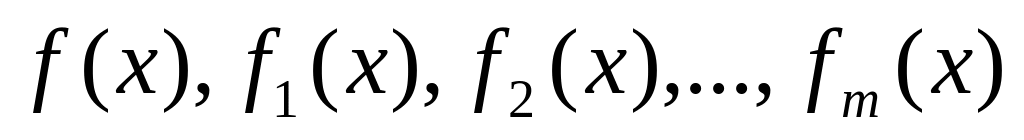 ,
где
сам полином,
,
где
сам полином,
 ,
,
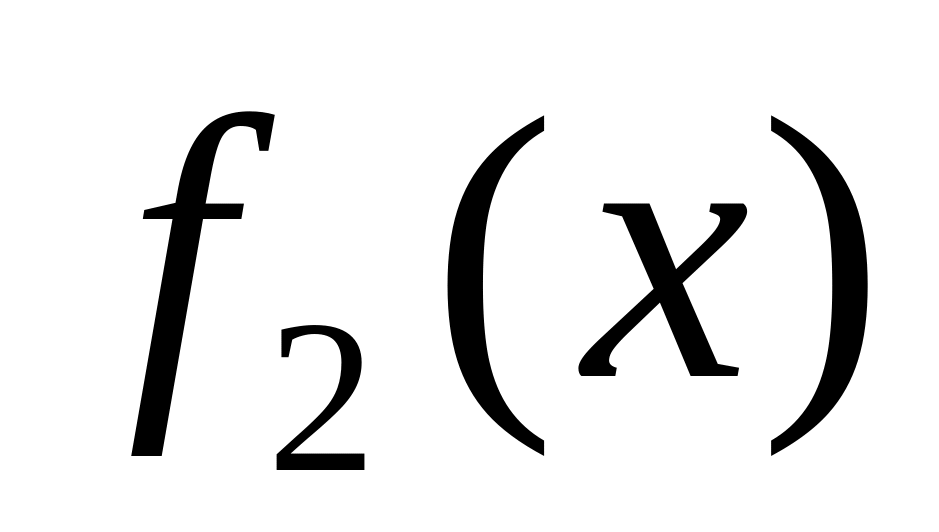 представляет собой взятый с обратным
знаком остаток от деления
на
представляет собой взятый с обратным
знаком остаток от деления
на
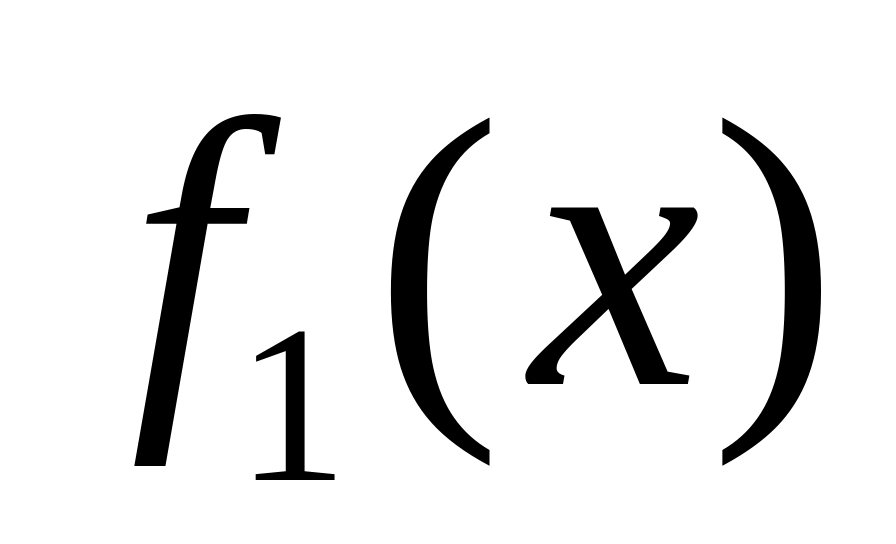 ,
,
 представляет собой взятый с обратным
знаком остаток от деления
на
и т.д.,
представляет собой взятый с обратным
знаком остаток от деления
на
и т.д.,
 представляет собой взятый с обратным
знаком остаток от деления
представляет собой взятый с обратным
знаком остаток от деления
 на
на
 .
.
Замечание.
Если полином
не имеет кратных корней, то
и последняя функция Штурма
![]() действительная ненулевая константа,
кроме того полиномы из системы Штурма
можно находить с точностью до положительного
множителя.
действительная ненулевая константа,
кроме того полиномы из системы Штурма
можно находить с точностью до положительного
множителя.
Далее обозначим через
![]() количество перемен знака в системе
многочленов Штурма при
количество перемен знака в системе
многочленов Штурма при
![]() ,
при условии, что нулевые элементы этой
системы вычеркнуты.
,
при условии, что нулевые элементы этой
системы вычеркнуты.
|
|
|
|
|
… |
|
|
|
+ |
0 |
- |
+ |
- |
+ |
4 |
Теорема Штурма.
Если
полином
-й
степени, не имеющий кратных корней на
интервале
![]() и
и
![]() ,
,
![]() ,
то количество действительных корней
уравнения
в точности равно количеству перемен
знаков в системе Штурма полинома
при переходе из точки
,
то количество действительных корней
уравнения
в точности равно количеству перемен
знаков в системе Штурма полинома
при переходе из точки
![]() в точку
в точку
![]() ,
то есть
,
то есть
![]() .
.
Замечание.
При помощи теоремы Штурма можно с успехом
отделять действительные корни
алгебраического уравнения (2),
разбивая исходный интервал
на достаточно тесные промежутки
![]() такие, что
такие, что
![]() .
.
Методы уточнения корней
Для уточнения корней нелинейного уравнения (1) на интервале, содержащем единственный корень данного уравнения, используются, как правило, итерационные методы:
метод половинного деления;
метод простой итерации;
метод касательных;
метод хорд.
Основная идея всех
итерационных методов состоит в том, что
исходя из некоторого начального
приближения
![]() строиться последовательность приближений
строиться последовательность приближений
![]() при определённых условиях сходящаяся
к корню
данного уравнения.
при определённых условиях сходящаяся
к корню
данного уравнения.
В силу указанной сходимости процесс построения приближения можно прервать на некотором шаге с достаточно большим номером итерации и объявить последнее из построенных приближений приближённым решением данного уравнения.
Определение.
Величина
![]() называется погрешностью итерационного
метода на
-й
итерации, где
называется погрешностью итерационного
метода на
-й
итерации, где
![]()
Определение.
Величина
![]() называется невязкой уравнения (1)
на приближенном решении
называется невязкой уравнения (1)
на приближенном решении
![]() .
.
Понятно, что если
итерационный метод сходится, то
последовательность погрешностей
![]() ,
а так же и последовательность невязок
,
а так же и последовательность невязок
![]() .
Верно и обратное утверждение.
.
Верно и обратное утверждение.
Скорость сходимости
Говорят, что итерационный
метод имеет линейную скорость сходимости
(или скорость сходимости геометрической
прогрессии со знаменателем
![]() ),
если, начиная с некоторого номера
итерации
,
выполняется следующее неравенство:
),
если, начиная с некоторого номера
итерации
,
выполняется следующее неравенство:
![]() ,
где
,
где
![]() .
Чем меньше
,
тем быстрее метод сходится.
.
Чем меньше
,
тем быстрее метод сходится.
Говорят, что итерационный
метод имеет сверхлинейную скорость
сходимости, если, начиная с некоторого
номера итерации
,
выполняется следующее неравенство:
![]() ,
где
,
где
![]() ,
,
![]() .
.
Говорят, что итерационный
метод имеет квадратичную скорость
сходимости, если, начиная с некоторого
номера итерации
,
выполняется следующее неравенство:
![]() ,
где
.
,
где
.
Квадратичная скорость сходимости самая быстрая.
Определим понятие
критерия окончания итерационного
процесса. Обычно на практике требуется
найти приближённое решение исходного
уравнения
(1) с
некоторой наперёд заданной точностью
![]() .
То есть выполнять вычисление приближений
итерационным методом до тех пор, пока
не выполниться условие:
.
То есть выполнять вычисление приближений
итерационным методом до тех пор, пока
не выполниться условие:
![]() (3) –
истинный критерий окончания. Однако на
практике точное значение корня
,
как правило, неизвестно, поэтому
пользуются другими критериями близкими
к истинному, либо же следующими, вообще
говоря, «ложными» критериями:
(3) –
истинный критерий окончания. Однако на
практике точное значение корня
,
как правило, неизвестно, поэтому
пользуются другими критериями близкими
к истинному, либо же следующими, вообще
говоря, «ложными» критериями:
![]() (4) или
(4) или
![]() (5).
Однако, из выполнения условий (4)
и (5),
вообще говоря, не следует выполнение
условия (3),
то есть выполнение условий (4)
и (5)
не гарантирует выполнение условия (3)
с той же точностью
(5).
Однако, из выполнения условий (4)
и (5),
вообще говоря, не следует выполнение
условия (3),
то есть выполнение условий (4)
и (5)
не гарантирует выполнение условия (3)
с той же точностью
![]() .
.
{ Самостоятельно законспектировать тему: «Метод половинного деления»}
Метод простой итерации (МПИ)
Пусть задано нелинейное уравнение (1) на интервале , содержащем один и только один корень данного уравнения.
Предположим, что непрерывная и имеет непрерывную производную на .
С помощью эквивалентных
преобразований приведём уравнение (1)
к виду удобному для итерирования:
![]() (2).
Например, домножим обе части уравнения
(1)
на
(2).
Например, домножим обе части уравнения
(1)
на
![]() к обеим частям равенства добавим
к обеим частям равенства добавим
![]() ,
тогда
,
тогда
![]() .
.
Выберем на промежутке
каким-либо способом, грубо, приближённое
значение корня
![]() и вычислим
и вычислим
![]() по формуле:
по формуле:
![]() - первое приближение к решению уравнения
(1)
(или что то же самое (2));
- первое приближение к решению уравнения
(1)
(или что то же самое (2));
Исходя из
построим
![]() по формуле:
по формуле:
![]() - второе приближение к решению уравнения
(1)
(или что то же самое (2))
и т.д. Если известно приближение
,
то
- второе приближение к решению уравнения
(1)
(или что то же самое (2))
и т.д. Если известно приближение
,
то
![]() ,
(3).
Формула (3)
описывает МПИ для решения уравнения
(1)
(или что то же самое (2)).
,
(3).
Формула (3)
описывает МПИ для решения уравнения
(1)
(или что то же самое (2)).
Говорят, что МПИ для
уравнения (1)
сходится, если предел последовательностей
приближений
![]() ,
определяемых формулой (3)
существует и равен точному значению
корня
:
,
определяемых формулой (3)
существует и равен точному значению
корня
:
![]() .
.
Выясним условия сходимости МПИ.
Теорема.
Пусть функция
определена и дифференцируема на
и принимает значения в этом промежутке
(![]() ).
Пусть кроме того
).
Пусть кроме того
![]() (4),
тогда МПИ (3)
сходится независимо от выбора начального
приближения
(4),
тогда МПИ (3)
сходится независимо от выбора начального
приближения
![]() к точному значению корня
уравнения (1) и
справедлива оценка погрешности:
к точному значению корня
уравнения (1) и
справедлива оценка погрешности:
![]() (5).
(5).
Из этой теоремы следует,
что в качестве
в частности можно взять максимум по
модулю значения функции
![]() на
:
на
:
![]() и чем меньше значение
,
тем выше фактическая скорость сходимости
метода. МПИ имеет линейную скорость
сходимости (или скорость сходимости
геометрической прогрессии с указанным
знаменателем
).
и чем меньше значение
,
тем выше фактическая скорость сходимости
метода. МПИ имеет линейную скорость
сходимости (или скорость сходимости
геометрической прогрессии с указанным
знаменателем
).
Из оценки погрешности
(5)
следует, что итерации в общем случае
следует продолжать до тех пор, пока не
выполнится условие:
![]() (6).
(6).
Условие (6)
называется критерием окончания
итерационного процесса, близким к
истинному, так как его выполнимость
гарантирует получение приближённого
решения
![]() с заданной точностью
(
по формуле (5)).
с заданной точностью
(
по формуле (5)).
Если функция
в исходном уравнении (1)
достаточно гладкая и
![]() не обращается в ноль ни в одной точке
отрезка, то можно получить ещё один
критерий близкий к истинному. Для этого
воспользуемся разложением функции
в ряд Тейлора в окрестности точки
:
не обращается в ноль ни в одной точке
отрезка, то можно получить ещё один
критерий близкий к истинному. Для этого
воспользуемся разложением функции
в ряд Тейлора в окрестности точки
:
![]() ,
где
,
где
![]() ,
.
,
.
![]() .
Возьмём
.
Возьмём
![]() ,
тогда
,
тогда![]() ,
где
,
так как
точное значение корня.
,
где
,
так как
точное значение корня.
![]() или
или
![]() .
Введём обозначения
.
Введём обозначения
![]() ,
тогда
,
тогда
![]() и в качестве критерия близкого к истинному
получаем:
и в качестве критерия близкого к истинному
получаем:
![]() (7).
(7).
Кроме критериев (6) и (7) можно так же пользоваться и ложными критериями приведенными ранее.
Если исходное уравнение
(1)
приведено к следующему эквивалентному
виду:
![]() ,
,
,
,
![]() ,
,
![]() ,
то МПИ (3)
для такого уравнения записывается
следующим образом:
,
то МПИ (3)
для такого уравнения записывается
следующим образом:
![]() (8).
В формуле (8)
константу
(8).
В формуле (8)
константу
![]() возьмём такую, чтоб последовательность
приближений в этой формуле была
сходящейся, для этого воспользуемся
теоремой о сходимости и потребуем, чтоб
возьмём такую, чтоб последовательность
приближений в этой формуле была
сходящейся, для этого воспользуемся
теоремой о сходимости и потребуем, чтоб
![]() :
:
![]()
![]()
Поскольку на промежутке содержится единственный корень уравнения , то функция на данном промежутке сохраняет свой знак, поэтому возможны 2 случая:
 функция сохраняет
положительный знак на
,
тогда
функция сохраняет
положительный знак на
,
тогда
 ;
;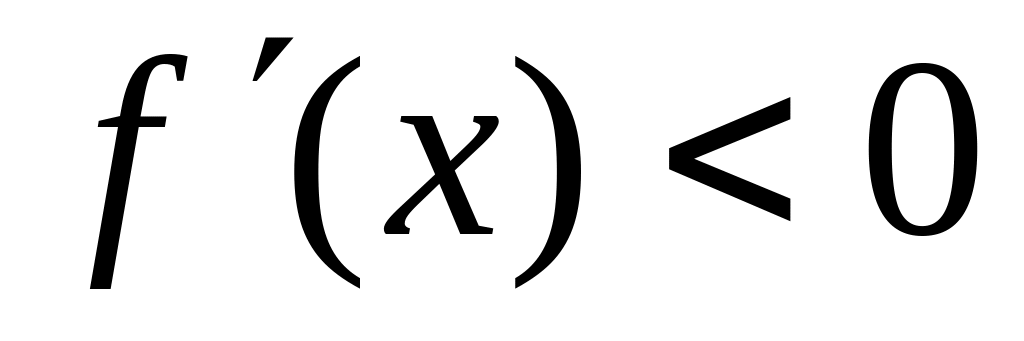 функция сохраняет
отрицательный знак на
,
функция сохраняет
отрицательный знак на
,
 тогда
тогда

Если
![]() ,
то
,
то
![]() при
и
при
и
![]() при
.
при
.
Подставляя в формулу (8) будем получать сходящийся итерационный метод.
Замечание. МПИ (8) сходится быстрее всего (знаменатель геометрической прогрессии принимает наименьшее возможное значение), если:
, то
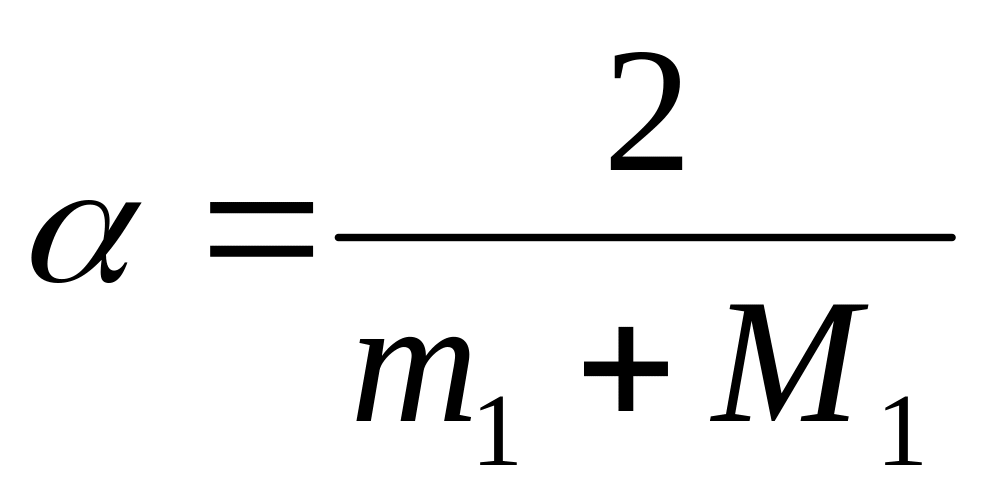
, то

Рассмотрим геометрический
смысл МПИ.
![]() ,
,
![]() - условие сходимости.
- условие сходимости.
сходимость по «лестнице»
 ,
,

сходимость по «спирали»


 расходящийся случай
расходящийся случай

Метод Ньютона (метод касательных)
Пусть задано нелинейное уравнение (1) на интервале , содержащем один и только один корень данного уравнения.
Предположим, что
непрерывно-дифференцируема на
,
![]() .
.
Получим итерационную формулу метода Ньютона аналитически. Пусть нам уже известно -е приближение решения уравнения (1)
Разложим функцию
в ряд Тейлора в окрестности точки
![]() :
:
. Возьмём в качестве точное значение корня ( ), тогда , где , так как точное значение корня.
,
![]() .
Тогда в качестве следующего приближения
.
Тогда в качестве следующего приближения
![]() к корню уравнения (1)
можно взять следующее выражение:
к корню уравнения (1)
можно взять следующее выражение:
![]() ,
(2)
– итерационная формула метода Ньютона.
,
(2)
– итерационная формула метода Ньютона.
Теорема (о сходимости).
Пусть
и
,
![]() существуют, непрерывны, сохраняют
определённые знаки на
и не обращаются в ноль, то есть
существуют, непрерывны, сохраняют
определённые знаки на
и не обращаются в ноль, то есть
![]() ,
,
![]() на
,
тогда если начальное приближение
удовлетворяет условию
:
на
,
тогда если начальное приближение
удовлетворяет условию
:![]() (3),
то метод Ньютона, определяемый формулой
(2),
сходится к
точному значению корня
уравнения (1)
и справедлива оценка погрешности:
(3),
то метод Ньютона, определяемый формулой
(2),
сходится к
точному значению корня
уравнения (1)
и справедлива оценка погрешности:
![]() (4),
где
и
(4),
где
и
![]() .
.
Следует отметить, что метод Ньютона для уравнения (1) обладает квадратичной скоростью сходимости, более быстрой чем линейная, однако метод сходится лишь в малой окрестности корня , то есть когда начальное приближение выбрано достаточно близко к корню .
Из оценки погрешности
(4)
можно получить критерий окончания
итерационного процесса, близкий к
истинному:
![]() (5).
Можно так же пользоваться полученными
ранее критериями :
- близкий к истинному, или двумя ложными
критериями
и
.
(5).
Можно так же пользоваться полученными
ранее критериями :
- близкий к истинному, или двумя ложными
критериями
и
.
Геометрический смысл метода Ньютона.
Пусть для определённости
,
![]() ,
,
,
,
![]() ,
,
![]() .
.

В качестве
начального приближения
точки
возьмём
![]() ,
так как
,
так как
![]() .
Проведём касательную к графику функции
в точке
.
Проведём касательную к графику функции
в точке
![]() до пересечения с осью
.
Уравнение касательной имеет вид
до пересечения с осью
.
Уравнение касательной имеет вид
![]() .
Точка пересечения касательной с осью
имеет координаты: абсцисса
.
Точка пересечения касательной с осью
имеет координаты: абсцисса
![]() ,
ордината
,
ордината
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
Значение абсциссы совпадает с итерационным
значением формулы (2)
при
.
Значение абсциссы совпадает с итерационным
значением формулы (2)
при
![]() .
Аналогично, из точки
находим точку с координатами
.
Аналогично, из точки
находим точку с координатами
![]() и через неё проводим касательную
и через неё проводим касательную
![]() ,
,
![]() и т.д. Таким образом, в качестве приближения
корня выступают абсциссы касательных.
и т.д. Таким образом, в качестве приближения
корня выступают абсциссы касательных.
Модифицированный метод Ньютона
Если
на
промежутке
изменяется несущественно, то в итерационной
формуле (2)
можно приближённо положить
![]() и тогда строить последовательность
приближений к решению по формуле:
и тогда строить последовательность
приближений к решению по формуле:
![]() ,
(6)
– итерационная формула модифицированного
метода Ньютона.
,
(6)
– итерационная формула модифицированного
метода Ньютона.
Достоинствами метода являются облегчение решения, уменьшение количества арифметических действий, однако, такая приближённая замена приводит к замедлению скорости сходимости – она становится линейной.
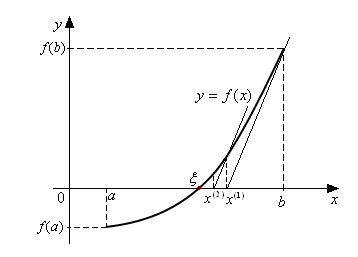
Геометрически касательные
к графику функции
в каждой точке
![]() заменяются прямыми параллельными
касательной в точке
заменяются прямыми параллельными
касательной в точке
![]() .
.
Метод хорд
Пусть задано нелинейное уравнение (1) на интервале , содержащем один и только один корень данного уравнения. Предположим, что функция дважды непрерывно-дифференцируема на , причём и сохраняют определённые знаки на .
Получим итерационную формулу метода хорд из геометрических соображений.
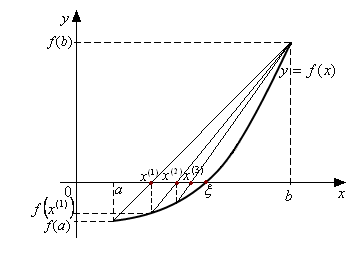
Пусть
,
,
,
.
Запишем уравнение хорды проходящей
через точки
![]() и
:
и
:
![]() .
Найдём точку пересечения хорды с осью
:
,
,
тогда
.
Найдём точку пересечения хорды с осью
:
,
,
тогда
![]() .
Далее проводим хорду через точки
и
,
получаем:
.
Далее проводим хорду через точки
и
,
получаем:
![]() ,
,
![]() ,
,
тогда
,
,
тогда
![]() .
Продолжая описанный процесс для
произвольного номера приближения
получаем:
.
Продолжая описанный процесс для
произвольного номера приближения
получаем:
![]() (2).
(2).
Начальным приближением
в формуле (2),
очевидно выступает точка
![]() .
В рассмотренном случае на промежутке
приближение к корню осуществляется
слева, правый же конец (точка
)
является неподвижным.
.
В рассмотренном случае на промежутке
приближение к корню осуществляется
слева, правый же конец (точка
)
является неподвижным.
Рассмотрим другой
случай:
,
,
,
![]() .
.
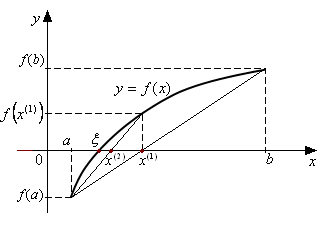
Так же как и в первом
случае проводим прямую соединяющую
точки
и
и т.д.
и
,
![]() В этом случае процесс приближения к
корню осуществляется справа, точка
выступает в качестве начального
приближения, а левая граница (точка
)
является неподвижной. Тогда итерационная
формула имеет вид:
В этом случае процесс приближения к
корню осуществляется справа, точка
выступает в качестве начального
приближения, а левая граница (точка
)
является неподвижной. Тогда итерационная
формула имеет вид:
![]() ,
(3).
,
(3).
Теорема (о сходимости).
Пусть
и
,
существуют, непрерывны, сохраняют
определённые знаки на
и не обращаются в ноль. Если начальное
приближение удовлетворяет условию
:![]() (4),
то метод хорд (2)
или (3) сходится
к точному значению корня
уравнения (1)
и справедлива оценка погрешности:
(4),
то метод хорд (2)
или (3) сходится
к точному значению корня
уравнения (1)
и справедлива оценка погрешности:
![]() (5),
где
и
(5),
где
и
![]() .
.
Из этой теоремы следует, что на отрезке , тот из концов отрезка ( или ) на котором знак функции совпадает со знаком является неподвижным и соответственно тот из концов, для которого выполняется условие (4) выступает в качестве начального приближения.
Из оценки погрешности
(5)
вытекает следующий критерий окончания
итерационного процесса, близкий к
истинному:
![]() (6).
(6).
Кроме условия (6) можно использовать полученный ранее критерий близкий к истинному , а так же использовать ложные критерии и .
В теории метода показано,
что если начальное приближение
![]() выбрано достаточно близко к корню
,
то метод хорд сходится с линейной
скоростью сходимости.
выбрано достаточно близко к корню
,
то метод хорд сходится с линейной
скоростью сходимости.
