Участок ав

Сечение А: N_А=–R_А=–(–27,5)=27,5кН; (растяжение)

Q_А=H_А=30кН; M_А=0.

Сечение В: N_В=–R_А=–27,5кН; (сжатие)

Q_В=H_А=30кН; M_В=Ha 3=30 3=90кНм.

Участок ВС

Сечение В: N_В=–F₁+H_А=–60+30=–30кН; (сжатие)

Q_В=R_В=27,5кН;

M_В=H_А 6=30 6=180кНм.

Сечение С: Nc=-F₁+H_А=–30кН;

Qc=Ra–q 4=27,5-80=-107,5кН;

Mc=Ra 4+Ha 6-q 4 2=-27,5 4+180-160=-90кНм.

В середине участка ВС:

Mx=Ra 2+Ha 6–q 2 1=27,5 2+180–20 2=–55+140=85кНм.

Участок DE

Сечение E: N_E=–Re=–107,5кН; Q_E=0; M_Е=0;

Сечение D: N_D=–Re=-107,5кН; Q_D=F₂=30 кН; M_D=0.

Участок DС

Сечение D: N_D=–R_Е=–107,5кН; Q_В=0; M_В=0.

Сечение С: Nc=–R_Е=-107,5кН; Qc=F₂=30кН; Mc=–F₂ 3=–30 3=–90кНм.

На рис.2.9 показаны эпюры Q, N и М.

Покажем внутренние усилия, действующие в узле С.

Уравнения статики ∑ Fх = 0, ∑ Fy = 0, ∑ М_с = 0 выполняются, следовательно узел С находится в равновесии

Пример 2.10. Построим эпюры Q, N и М для кривого бруса, показанном на рис.2.10.

Для консольного кривого бруса можно построить эпюры Q, N и М без определения опорных реакций H_A, R_A и М_Е начиная со свободного конца.

Участок DС (прямолинейный)

Сечение D: N_D=0; Q_D=F=30кН; M_D=0;

Сечение С: Nc=0; Qc=F=30кН; Mc= –F 1=–30кНм.

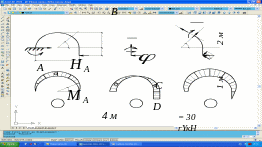
Рис.13

Рис.2.10

Рис.

Рис.2.10 а

Рис.2.10а

Участок СВА (криволинейный)

N=–F sinφ=–30sinφ;

Q=F cosφ=30cosφ; Mx=–F(1+2sinφ)=–30(1+2sinφ).

Задавая углу  интервал 30°, определим значения Q, N и М в сечениях

=0; N_С=0 ;Q_С=30 кН; М_С=–30 кНм.

j=30°; N=–15 кН; Q=25,98 кН; М=–60 кНм.

j=60°; N=–25,98 кН; Q=15 кН; М=–81,96 кНм.

j=90°; N_В=–30 кН; Q_В=0; М_В=–90 кНм.

j=120°; N=–25,98 кН; Q=–15 кН; М=–81,96 кНм.

j=150°; N=–15 кН; Q=–25,98 кН; М=–60 кНм.

j=180°; N_А=0; Q_А=–30кН; М_А=–30 кНм.

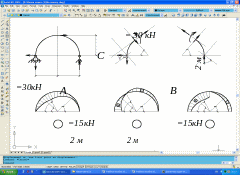
Эпюры Q, N и М показаны на рис.2.10 а.

Пример 2.11. Построить эпюры М, Q и N для шарнирно опёртого кривого бруса, изображенного на рис.2.11.

Опорные реакции определяем из уравнений статики.

∑ Fx=0; –H_А+F=0; H_А=F=30кН;

∑ M_В=0; R_А 4–F 2=0; R_А=15кН;

∑ M_А=0; R_В 4–F 2=0; R_В=15кН.

Проверка: ∑ Fy=–R_А+R_В=0; –15+15=0; 0=0.

Следовательно, опорные реакции определены правильно.

Разобьем брус на два участка АС (1-й участок) и СВ (2-й участок)

Рассечем брус плоскостью 1–1, нормально к оси и рассмотрим равновесие левой части. Внутренние силовые факторы: продольная сила, поперечная сила и изгибающий момент определяются из уравнений равновесия

Nφ=30 sinφ₁+15cosφ₁; Qφ=30 cosφ₁–15sinφ₁;

Mφ=30 2sinφ₁–15 2(1–cosφ₁), 0≤φ₁ ≤90^▫.

Определим экстремальные значения Mφ и Nφ на участке АС в сечении 2-2

Qφ=30cosφ₀-15sinφ₀; φ₀=63°27^’.

Mэкс=60 sinφ₀–30(1–0.5φ₀)=60 0,894–30(1–0,447)=37,05кНм.

Nэкс=30 sinφ₀+15cosφ₀=30+15 .0,447=33.54кН;

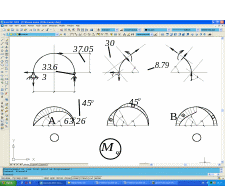
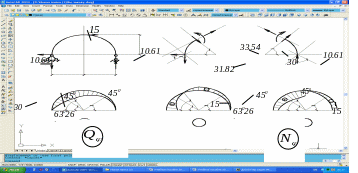
Рис.2.11 а

Выражение силовых факторов для сечения ВС имеют вид:

Nφ=-R_В cosφ₂; Qφ=-R_В sinφ₂;

Mφ=R_В 2(1-cosφ₂) 0 ≤φ₂≤90^▫

На основании полученных выражений и значений Nφ, Qφ и Mφ в сечениях φ=0, 45°, 63°26^’, 90° построены эпюры изгибающих моментов, поперечных и продольных сил (рис. 2.11 а).