Участок ас

Сечение А: Q_А=R_А=40кH; M_А=0;

Сечение С: Qc=R_А–q 4=40-15 4=–20кH;

Mc=R_А 4–q 4 2=40 4–15 2 4=40 кНм.

На участке АС действует равномерно распределенная нагрузка, поэтому изгибающий момент М_X изменяется по закону параболы.

Для нахождения экстремального значения Мx определим положение сечения балки, в котором поперечная сила Q_у =0:.

Q = R_А–q z₀=0.

Откуда находим z₀ = R_А/q=40/15=2,67м.

В этом сечении изгибающий момент принимает экстремальное значение. М_х^экс = R_А z–q z₀ z₀/2=40 2.67–15 2.67²/2=53,33кНм.

Участок ВС (справа)

Сечение В: Q_В=–R_В=–35кH; M_В=–M=30кHм.

Сечение С: Qc=–R_В=–35кH; Mc=R_В 2–M=35 2–30=40кHм.

Эпюры Q и М_х показаны на рис.2.3.

В опасном сечении Q =0 и М_х =53,33 кНм.

Пример 2.4. Построим эпюры Q и М_х для однопролётной балки с консолями, изображенной на рис. 2.4.

Из уравнений статики определяем опорные реакции.

∑ M_В=0; –R_А 6+q 6 (6/2+2)–M–F 1.5=0;

R_А=(15 6 5–30–20 1,5)/6=65кH;

∑ M_А=0; R_В 6–F 7.5–M–q 6 (6/2–2)=0; R_В=(20 7.5+30+15 6 1)/6=45кH.

Для проверки спроектируем все силы на вертикальную ось у:

∑ Fy =0; –65+15 6–45+20=0.

Следовательно, опорные реакции определены правильно.

Вычисляем поперечные силы и изгибающие моменты в характерных сечениях

Участок ас

Сечение А: Q_А=–q 2=–15 2=–30кH;

M_А=–q 2 1=–15 2 1=–30кHм.

Сечение С: Qc=0; Mc=0.

Рис.2.4

Найдем значение изгибающего момента в середине участка АС:

М_х = –q 1 1/2=–7.5кHм.

Участок AD

Сечение А: Q_А=–q 2+Ra=–15 2+65=35кH;

M_А=–q 2 1=–15 2 1=–30кHм.

(Растянуты верхние волокна)

Сечение D: Q_D= R_А–q 6=65–15 6=–25кН.

M_В=R_А 4–q 6 6/2=65 4–15 6²/2=–10кHм.

Для нахождения экстремального значения Мх определим положение сечения балки, в котором поперечная сила Q_у =0:.

Q=–q z₀+R_А=0; –15z₀+65=0;

Откуда находим z₀=65/15=4,33м

В этом сечении изгибающий момент изменяет экстремальное значение

M_экс=–q z₀²/2+R_А (z₀–2)= –15 4,33²/2+65 2,33=10,83кHм.

Участок ве

Сечение Е: Q_Е=F=20кH; M_Е=0.

Сечение В: Q_В=F=20кН; M_В=–F 1,5=–20 1,5=–30кHм.

Участок ВD

Q_В=F–R_В=20–45=–25кН; M_В=–20 1.5=–30кHм;

Q_D=F–R_В=20–45= –25кН; M_D=–F 3,5+R_D 2= –20 3.5+45 2=20кНм.

В опасном сечении Q=35 кН; М_х = –30 кН∙м.

Эпюры Q и М_х показаны на рис.2.4.

Пример2.5. Построить эпюры Q_у и М_х для балки с промежуточным шарниром С, показанной на рис.2.5.

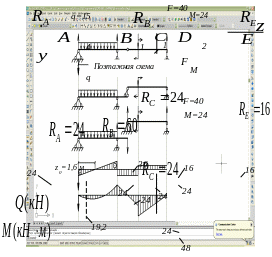
Рис.8

Рис.2.5

Решение. Расчетную схему балки с промежуточным шарниром можно представить в виде так называемой поэтажной схемы, в которой выделяется несомая часть балки СЕ и несущая часть АС. Вначале необходимо сделать расчет несомой балки СЕ.

Определим опорные реакций балки СЕ.

∑М_Е = –Rc 4–M+F 3=0;–Rc 4–4+40 3=0; Rc=96/4=24кН;

∑М_С = R_Е 4–F 1–M=0; R_Е 4–40 1–24=0; R_E=64/4=16 кН

Для проверки спроектируем все силы на вертикальную ось:

= 0; –Rc–R_Е+F=0; –24–16+40=0.

Опорные реакции определены правильно.

Вычисляем Q и М в характерных сечениях балки СЕ.

Участок СD

Сечение C: Q_C=R_C=24кН; Mc=0;

Сечение D: Q_D=–Rc=24кН; M_D=R_D 1=24 1=24кНм.

Участок ED

Сечение E: Q_Е=R_Е=–16кН; Me=0.

Сечение D: Q_D=–R_Е=–16кН; M_D=R_Е 3=16 3=48кНм.

Несущая часть балки АВС рассчитывается на действие распределений нагрузки q=15 кН/м и силы, численно равной опорной реакции балки СЕ R_C=24 кН и направленной в противоположную сторону.

Определим опорные реакции несущей балки АС.

∑М_А =R_В 4–R_С 5–q 4 2=0; –R_В 4–24 5–15 4 2=0; R_В=240/4=60кН;

∑М_В = –R_С 1+q 4 2–R_А 4 =0; –R_А 4 +15 4 2–24 1=0; R_А=96/4=24кН;

Для проверки спроектируем все силы на вертикальную ось:

∑Fy = 0; –R_А–R_В+q 4+R_C=0; –24–60+60+24=0.

Опорные реакции определены правильно.

Вычисляем Q и М в характерных сечениях балки АВС.

Участок СВ

Сечение C: Q_C=R_C=24кН; Mc=0;

Сечение В: Q_В=Rc=24кН; M_В=R_С 1=24 1=24кНм.

Участок АВ

Сечение А: Q_А=R_А=24кН; M_А=0.

Сечение В: Q_В=R_А –q 4 =24 –15 4=36кН;

M_В=R_А 4–q 4 2=24 4–15 4 2=24кНм.

Для нахождения экстремального значения Мх определим положение сечения балки, в котором поперечная сила Q_у =0:.

Q=–q z₀+R_А=0; –15z₀+24=0.

Откуда находим z₀=24/15=1,6м

В этом сечении изгибающий момент принимает экстремальное значение M_экс=R_А z₀–q z₀²/2+=24 1,6–15 1,6² /2=19,2кHм.

Эпюры М и Q приведены на рис 2.5.

Пример 2.6. Построить эпюры Q_у и М_х для балки с промежуточным шарниром, показанной на рис.2,6.

Решение. Расчетную схему балки представим в виде поэтажной

схемы, в которой выделяется несомая часть балки СЕ и несущая часть АС. Несомая балка опирается на несущую в точке С.

Вначале необходимо сделать расчёт несомой балки. Действие сосредоточенной силы F учтём при расчете этой балки.

Определим опорные реакции R_С и R_D несомой балки:

∑ М_D=F 3–Rc 3–q 1 1/2=0; 30 3–Rc 3–20 1 0.5=0; Rc=26,67кН;

∑ М_С= –q 1(3+0.5)+R_D 3=0; –20 1 3,5+R_D 3=0; R_D=23,33кН.

Проверка. ∑ F_y=0; F–Rc–R_D+q 1=0; 30–26,67–23,33+20 1=0; 0=0.

Следовательно, опорные реакции определены правильно.

Рис.2.6

Вычисляем Q_у и М_х в характерных сечениях несомой балки СЕ.

Участок СD

Сечение C: Qc=–F+Rc=–30+26,67=–3,33кН; Mc=0.

Сечение D: Q_D==3,33кН; M_D=–F 3+Rc 3= –30 3+26,67 3= –10кНм.

Участок ED

Сечение E: Q_Е=0; Me=0.

Сечение D: Q_D= q 1=20 1=20кН; M_D= –q 1 1/2=–20 1/2=–10кНм.

Вычисляем Q_у и М_х в характерных сечениях несущей балки АС.

Участок ВС

Сечение С: Qc=Rc=26,67кН; Mc=0.

Сечение В: Q_В=Rc=26,67кН; M_В=Rc 1= –26,67 1=26,67кНм.