Теорема Фалеса (доказательство).
Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Доказательство (задача №385 на стр. 105)
Подобные треугольники (определение). Признаки подобия треугольников.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Первый признак подобия: если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. (доказательство на странице 142)
Второй признак подобия: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны. (доказательство на странице 143)
Третий признак подобия: если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны. (доказательство на странице 144).
Отношение площадей подобных треугольников.
Отношение площадей 2 подобных треугольников равно квадрату коэффициента подобия.
Коэффициент подобия - это число, равное отношению сходственных сторон в подобных фигурах
Формулы площади треугольника. Отношение площадей треугольников с равными высотами.
1) S=1/2*a*h, где а – основание, h – высота («половина произведения основания на высоту»).
2) S=1/2*a*b, где a и b – катеты прямоугольного треугольника («половина произведения катетов»).
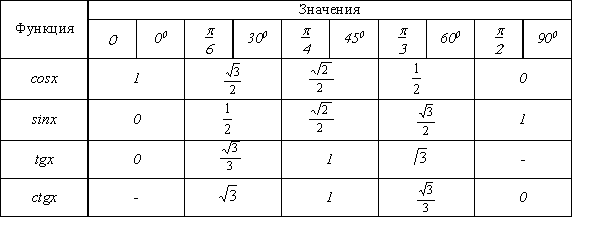
Синус острого угла прямоугольного треугольника: определение, значения некоторых углов (30°, 45° и 60°).
Синусом (sin) острого угла прямоугольного ∆ называется отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника: определение, значения некоторых углов (30°, 45° и 60°).
Косинусом (cos) острого угла прямоугольного ∆ называется отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника: определение, значения некоторых углов (30°, 45° и 60°).
Тангенсом (tg) острого угла прямоугольного ∆ называется отношение противолежащего катета к прилежащему катету.
